 |
Znanstveno-stručni
časopis Hrvatskog društva za geometriju i grafiku Scientific and Professional Journal |
|
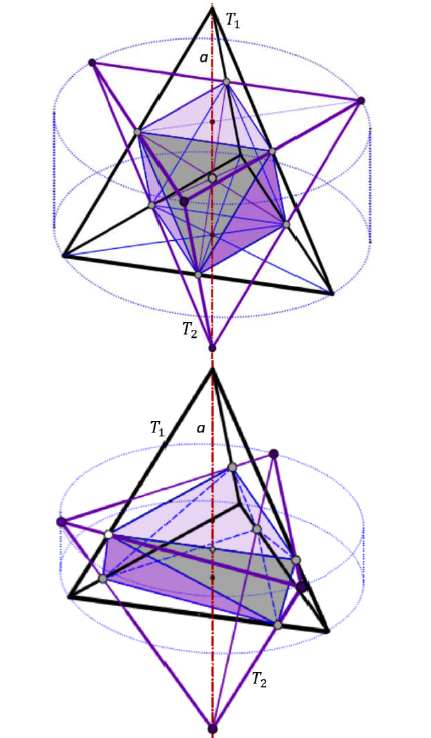
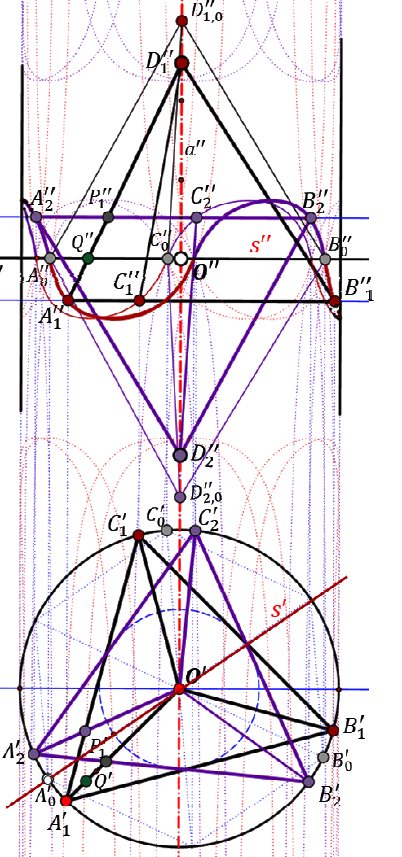
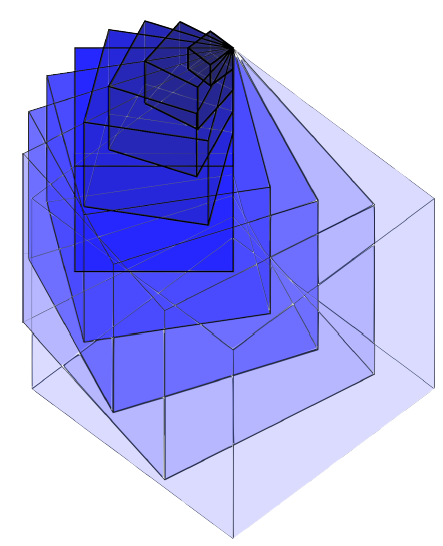
| Hellmuth Stachel, Gunter Weiss(stachel@dmg.tuwien.ac.at, weissgunter@gmx.net)
Zvjezdasti oktaedri (Stellae Octangulae) u pokretu - ponovno razmatranjeDobro je poznato da dva tetraedra T1 i T2 koji tvore zvjezdasti oktaedar (Stella Octangula) dopuštaju neprekidno gibanje tetraedra T2 s obzirom na tetraedar T1 takvo da svaki brid tetraedra T2 klizi duž brida tetraedra T1. Nedavno je isto svojstvo potvrđeno za parove (T1, T2) indirektno sukladnih tetraedara općeg oblika. Pokazuje se da taj prenapregnuti kinematički sustav, osim nekih posebnih jednoparametraskih gibanja, dopušta i dvoparametarska gibanja. Dajemo sintetičku analizu problema. Na temelju uključenih kvadrika detaljno proučavamo dvoparametarska gibanja i njihove granice. Osim toga, predstavljamo neka poopćenja zvjezdastih oktaedara. |
|
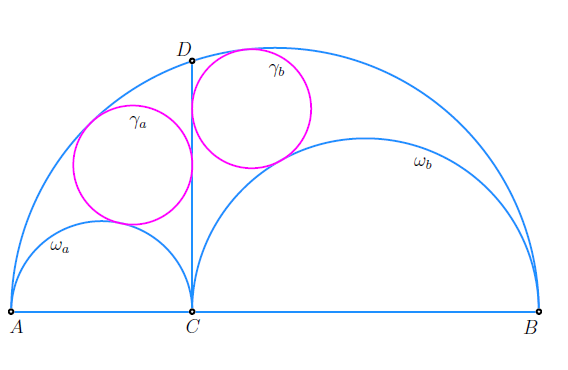
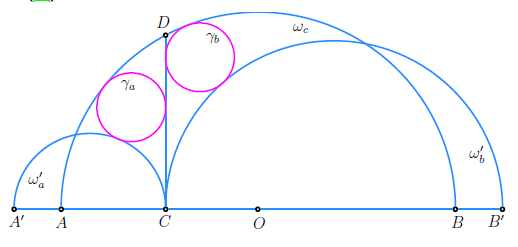
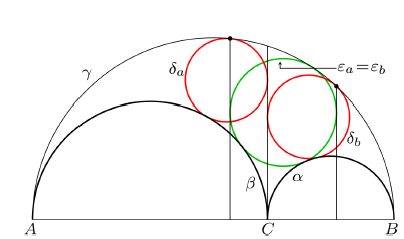
| Quang Hung Tran, Nikolaos Dergiades (tranquanghung@hus.edu.vn, ndergiades@yahoo.grt)
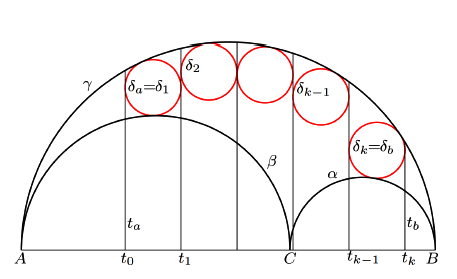
Poopćenje Arhimedovih kružnica na arbelosuU ovom radu proširujemo klasičan pojam Arhimedovih kružnica, koji je izvorno otkrio Arhimed na arbelosu, na širi okvir arbelosa s produžetkom. Pomoću novih konstrukcija odreujemo uvjete pod kojima kružnice u ovom poopćenom okruženju zadržavaju karakteristično svojstvo polumjera Arhimedovih kružnica. Naši rezultati ujedinjuju i proširuju prethodne rezultate, otkrivajući dublje simetrije i strukturne invarijante unutar ovih geometrijskih figura.Ključne riječi: Arhimedove kružnice, arbelos, arbelos s produžetkom  Article in PDF. Article in PDF. |
|
|
Mandi Orlić Bachler (mandi.orlic@tvz.hr)
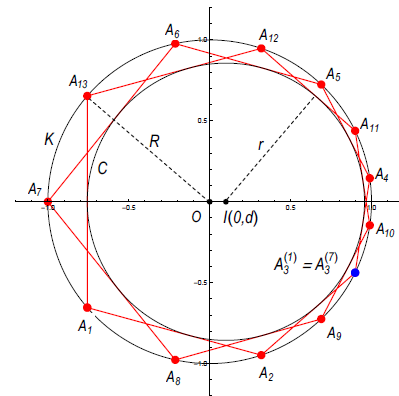
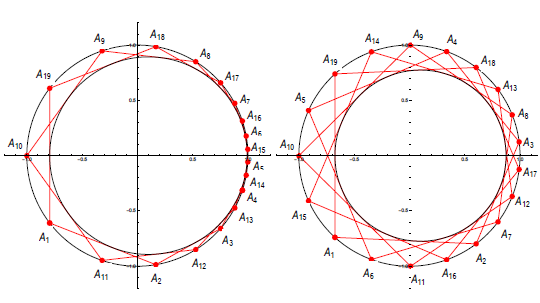
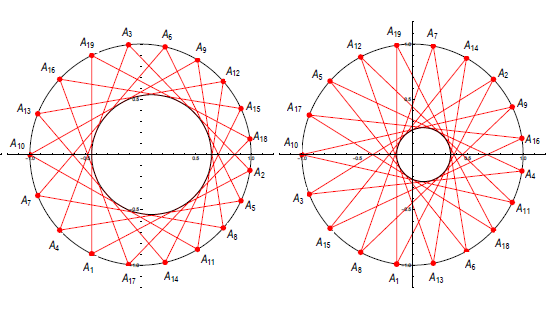
O Fussovim relacijama za bicentrične poligone s neparnim brojem vrhovaU radu su izvedeni analitički oblici Fussovih relacija za bicentrične poligone s neparnim brojem stranica i višim brojevima
rotacije. Metoda se temelji na Ponceletovom teoremu
te Radićevom teoremu i slutnji u vezi s povezanošći
Fussovih relacija za različite brojeve rotacije. Dobiveni su
eksplicitni analitički izrazi za bicentrični trinaesterokut s
rotacijskim brojem k = 2,4,6 i za bicentrični petnaesterokut
s rotacijskim brojem k = 2, dok su uspostavljeni
kompletni skupovi relacija za bicentrični sedamneasterokut
(za k = 1,2,3, 4,5,6,7,8) i devetnaesterokut (za k=1,2,3,4,5,6,7,8,9). Predloženi pristup pojednostavljuje
izvođenje i omogućuje sustavno proširenje poznatih Fussovih
relacija na bicentrične poligone višeg reda i nove brojeve
rotacije, čime se potvrđuje valjanost Radićeve slutnje. |
|
| Hiroshi Okumura
(hokmr@yandex.com)
Poopćenje Arhimedovih kružnica blizanacaU radu proučavamo arbelose i dajemo poopćenje Arhimedovih kružnica i Arhimedovih kružnica blizanaca. |
|
|
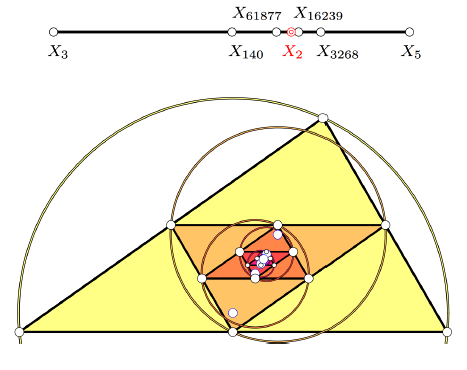
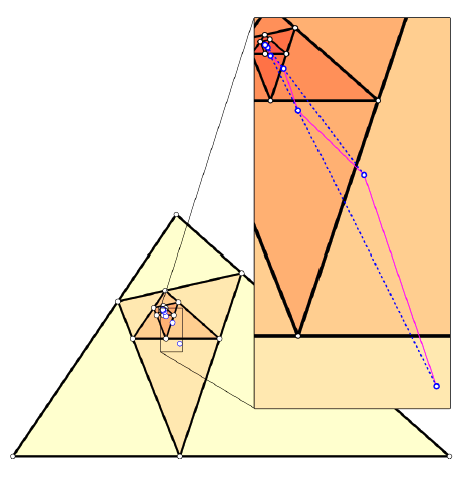
Christian Clemenz, Boris Odehnal (christian.clemenz@uni-ak.ac.at, boris.odehnal@uni-ak.ac.at)
Granične vrijednosti središta trokutaKonstrukcija središta trokuta uvijek stvara središnje trokute koji ponovno omogućavaju konstrukciju odgovarajućeg središta. Ponavljanje ovog postupka beskonačno mnogo puta može u pojedinim slučajevima dovesti do poznatog središta trokuta, ali u velikoj većini slučajeva pojavit će se novo središte. Simbolički računski pristup je ograničen u mnogim slučajevima zbog složenosti izračuna. Kako bismo prevladali te teškoće, započet ćemo s numeričkim pristupima prema graničnim vrijednostima nekoliko središta. To dovodi do nekih pretpostavki koje kasnije omogućavaju točno određivanje granične vrijednosti središta trokuta.
|
|
|
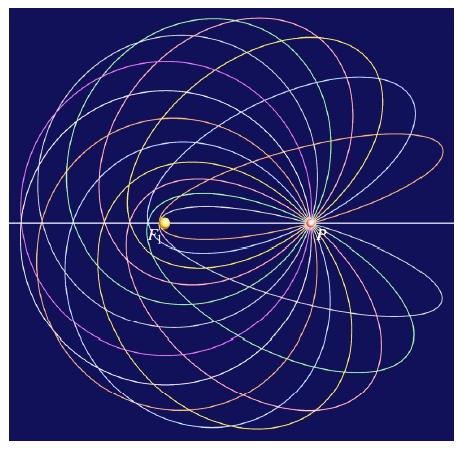
Georg Glaeser (georg.glaeser@uni-ak.ac.at)
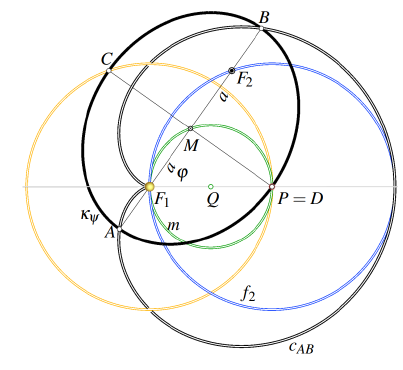
Geometrijska konstrukcija familije Keplerovih elipsaIstražujemo jednoparametarsku familiju Keplerovih elipsa u ravnini koje imaju isto žarište F1 i prolaze kroz danu točku P jednakom trenutnom brzinom. Pomoću čisto geometrijske konstrukcije – refleksija zrake F1P na tangenti u točki P – drugo žarište F2 leži na kružnici f2, dobivaju se geometrijska mjesta središta M i sporednih tjemena C, D (dvije kružnice) i glavnih tjemena A, B (konhoide kružnice). Familija elipsi ima envelopu, također elipsu, čije su poluosi dobivene u zatvorenoj formi. Ova konfiguracija pruža izravno geometrijsko tumačenje vis-viva relacije: Svi članovi dijele istu veliku glavnu poluos a, pa onda i isti orbitni period. Kada rotiraju oko osi F1P , elipse envelope tvore familiju konfokalnih rotacijskih elipsoida, čime se ravninska Keplerova konstrukcija povezuje s klasicnom geometrijom kvadrika.
|
|
|
Boris Odehnal (boris.odehnal@uni-ak.ac.at)
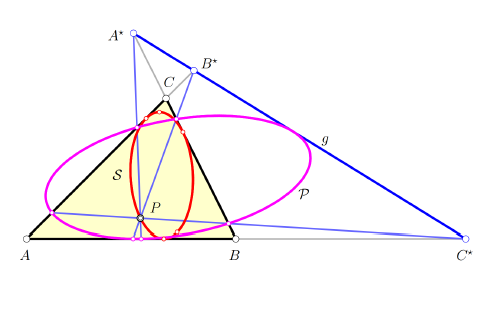
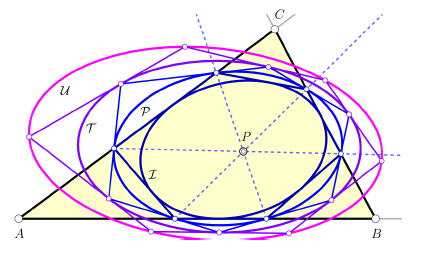
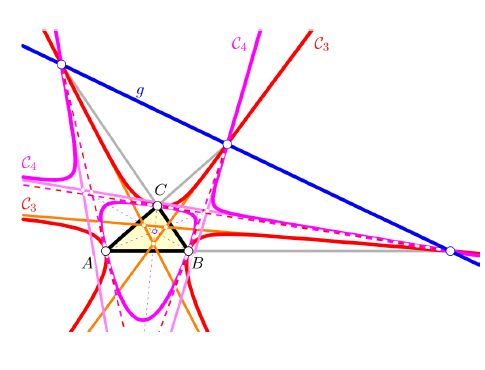
Projektivne paralelijane i s njima povezane porizmeDajemo projektivno poopćenje konstrukcije paralelijana i tako definiranih konika. Za bilo koju dobro odabranu točcku P i pravac g u ravnini trokuta Δ = ABC konstruiramo šest točaka koje uvijek leže na jednoj konici P, paralelijanskoj konici P točke P s obzirom na trokut Δ. Nadalje, nalazimo paralelijansku tangentnu koniku T , paralelijansku upisanu koniku I i dvije daljnje konike D i J koje su prirodno povezane s Δ i P. Bilo koji par ovih konika rezultira određenom porizmom, pa čak i lancem porizmi pomoću polarizacije. Proučavamo regularnost i singularnost kao i posebne položaje ovih konika prema pravcu g ovisno o izboru polazne točke P i pravca g. Također, dajemo detaljno istraživanje skupova mogućih polaznih točaka koje mijenjaju trokutaste ili šesterokutne porizme bilo kojeg para konika u porizme s jednoparametarskim familijama četverokuta i peterokuta.
|
|
|
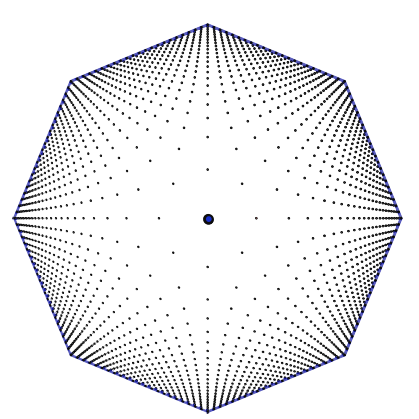
Iva Kodrnja (iva.kodrnja@geof.unizg.hr)
O izuzetnim svojstvima broja 2025U ovom članku proučava se broj 2025 i vizualizira njegova regularnost. Ovaj broj je potpuni kvadrat, a dubljim uvidom otkrivamo bogatu strukturu i povezujemo je s prebrojavanjem cjelobrojnih točcaka u poligonalnim domenama. Također dajemo osvrt na frekvenciju pojave kvadratnih i regularnih godina te jedinstvenost ovakve regularne godine.
|