 |
Znanstveno-stručni
časopis Hrvatskog društva za geometriju i grafiku Scientific and Professional Journal |
|
|
Hellmuth Stachel, Gunter Weiss(stachel@dmg.tuwien.ac.at, weissgunter@gmx.net)
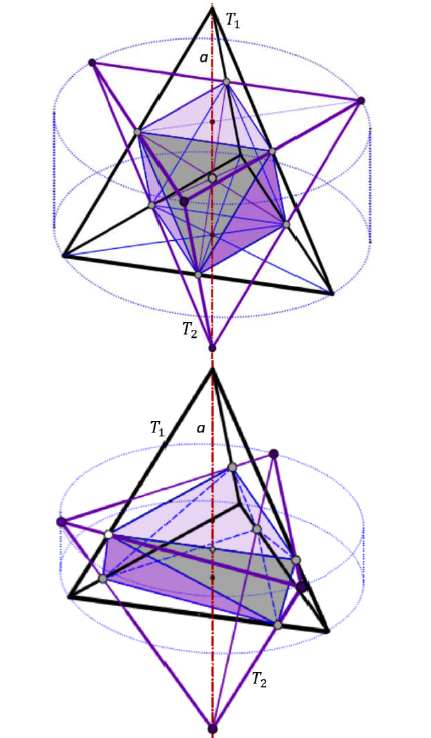
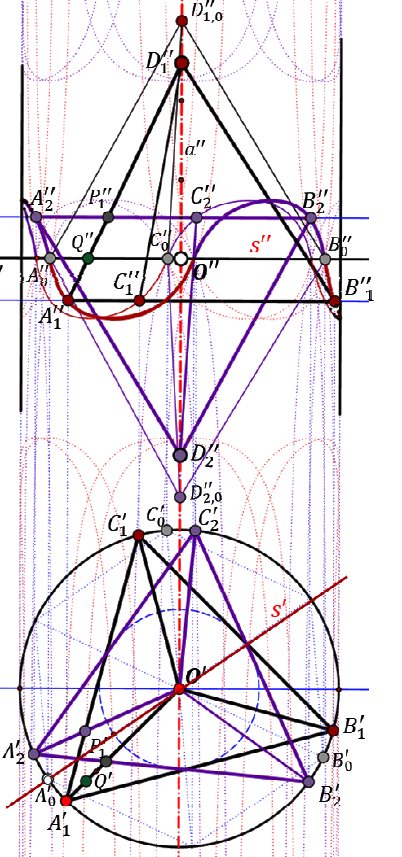
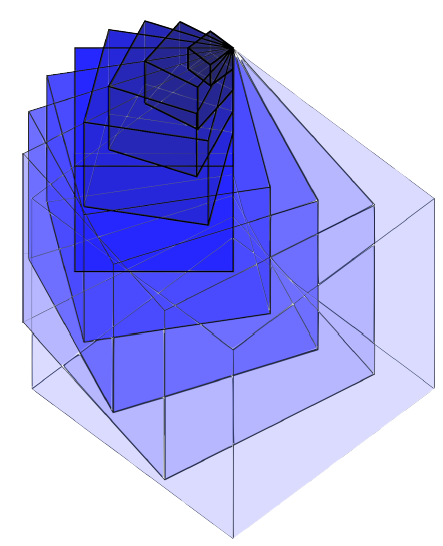
Stellae Octangulae in Motion RevisitedIt is well-known that two congruent regular tetrahedra T1
and T2 forming a Stella Octangula allow a continuous motion
of T2 relative to T1 such that each edge of T2 slides
along an edge of T1. Recently the same property has been
confirmed for pairs (T1, T2) of indirect congruent tetrahedra
of general form. It turns out that this overconstrained kinematical
systems admits besides some special one-parameter
motions also two-parameter motions. We provide a synthetic
analysis of the problem. Based on involved quadrics,
we study in depth the two-parameter motions and their
boundaries. Moreover, we present some generalizations of
Stellae Octangulae.
 Article in PDF. Article in PDF. |
|
| Quang Hung Tran, Nikolaos Dergiades (tranquanghung@hus.edu.vn, ndergiades@yahoo.grt)
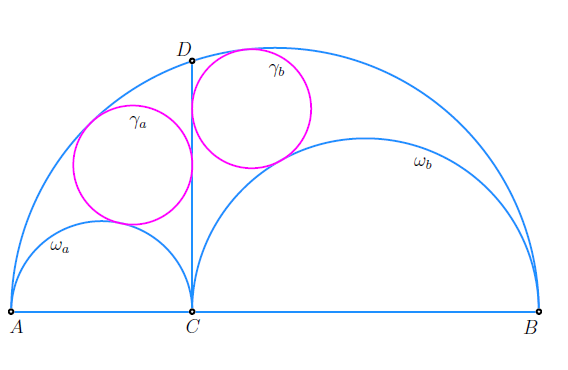
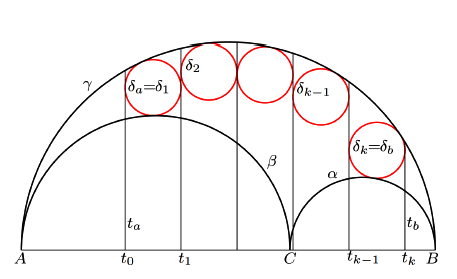
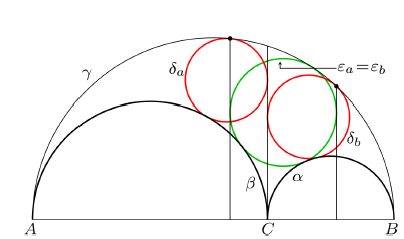
A Generalization of Archimedean Circles on an ArbelosIn this paper, we extend the classical notion of Archimedean
circles, originally discovered by Archimedes in the arbelos,
to the broader framework of the arbelos with overhang.
By means of new constructions, we establish conditions
under which circles in this generalized setting retain the
characteristic radius property of Archimedean circles. Our
results unify and extend previous findings, revealing deeper
symmetries and structural invariants within these geometric
figures. |
|
| Mandi Orlić Bachler (mandi.orlic@tvz.hr)
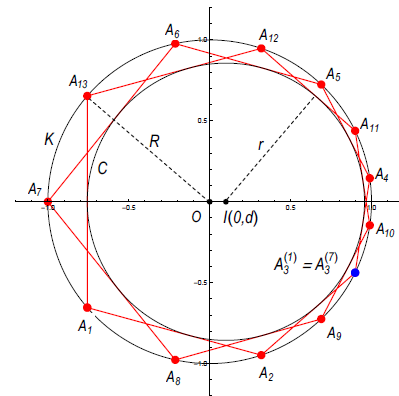
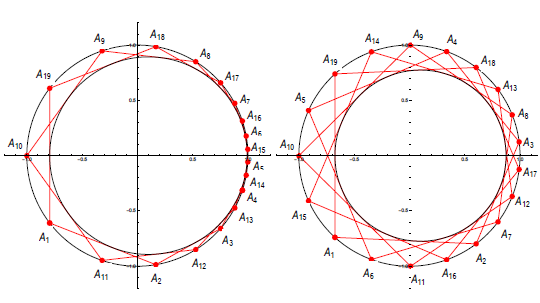
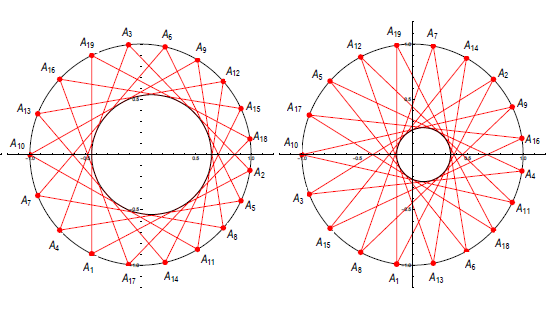
On Fuss’ Relations for Bicentric Polygons with an Odd Number of VerticesThis paper presents novel analytical forms of Fuss’ relations for bicentric polygons with an odd number of sides and higher rotation numbers. The method is based on Poncelet’s theorem and Radi´c’s theorem and conjecture concerning the connection between Fuss’ relations for different rotation numbers. Explicit analytical expressions are obtained for the bicentric triskaidecagon with k = 2,4,6 and for the bicentric pentadecagon with k = 2, while complete sets of relations are established for the bicentric heptadecagon (k = 1,2,3,4,5,6,7,8) and enneadecagon (k =1,2,3,4,5,6, 7,8,9). The proposed approach simplifies the derivation and enables a systematic extension of known Fuss’ relations to higher-order bicentric polygons and new rotation Key words: bicentric polygon, Fuss’ relation, rotation
number, triskaidecagon, pentadecagon, heptadecagon, enneadecagon |
|
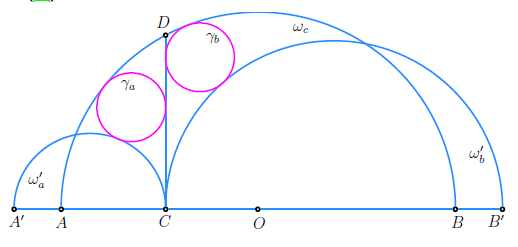
| Hiroshi Okumura
(hokmr@yandex.com)
A Generalization of the Twin Circles of ArchimedesWe consider the arbelos and generalize Archimedean circles
and the twin circles of Archimedes. |
|
|
Christian Clemenz, Boris Odehnal (christian.clemenz@uni-ak.ac.at, boris.odehnal@uni-ak.ac.at)
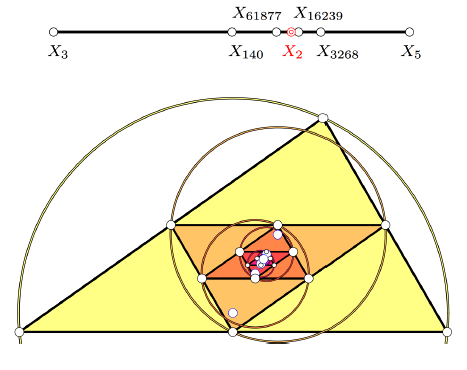
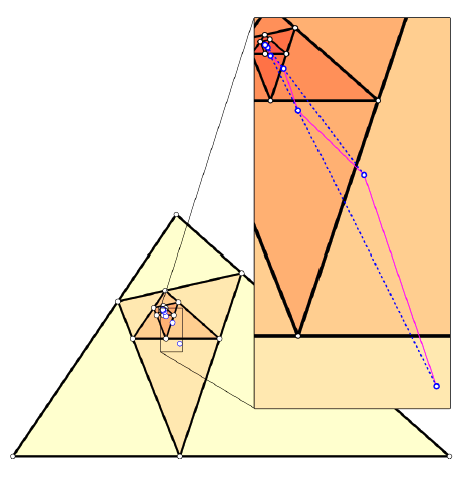
Limits of Triangle CentersThe construction of a triangle center always produces central triangles which again allow for the construction of the respective center. Doing this infinitely many times may in some cases lead to a known triangle center, but in the vast majority, a new center will show up. The symbolic computational approach is limited in many cases due to the complexity of the computations. In order to overcome these difficulties, we shall start with numerical approaches towards several centers’ limits. This gives rise to some conjectures which later allow for an exact determination of the limit of a triangle center. Key words: triangle center, iterated construction, numerical
simulation, limit |
|
|
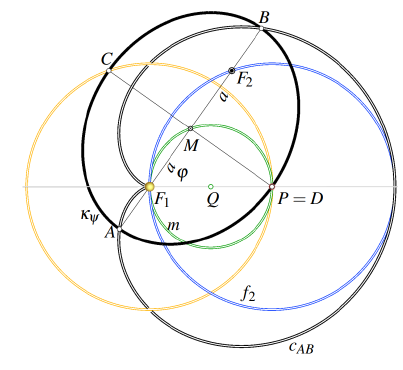
Georg Glaeser (georg.glaeser@uni-ak.ac.at)
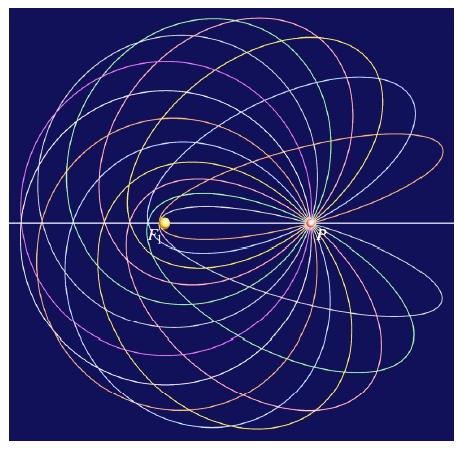
A Geometric Construction of a Family of Keplerian EllipsesWe investigate a one-parameter family of Keplerian ellipses in a plane sharing a fixed focus F1 and passing through a prescribed point P with identical instantaneous speed. By means of a purely geometric construction – the reflection of the ray F1P in the tangent at P – the second focus F2 is located on a circle f2, yielding simple loci for the centers M and the secondary vertices C,D (both circles) and for the principal vertices A,B (conchoids of a circle). The family admits an envelope, itself an ellipse whose semiaxes are obtained in closed form. The configuration provides a direct geometric interpretation of the vis-viva relation: All members share the same semimajor axis a, and thus, the same orbital period. When rotated about the axis F1P, the envelope ellipses form a family of confocal ellipsoids of revolution, thus connecting the planar Kepler construction with the classical geometry of quadrics. Key words:
Keplerian ellipses, envelope ellipse, conchoid,
limacon, vis-viva relation, energy equation |
|
|
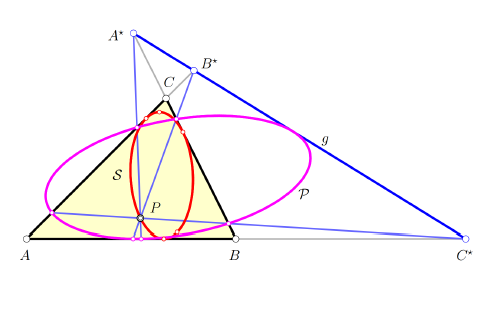
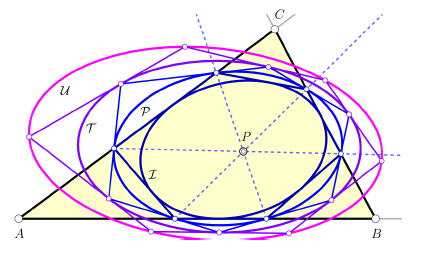
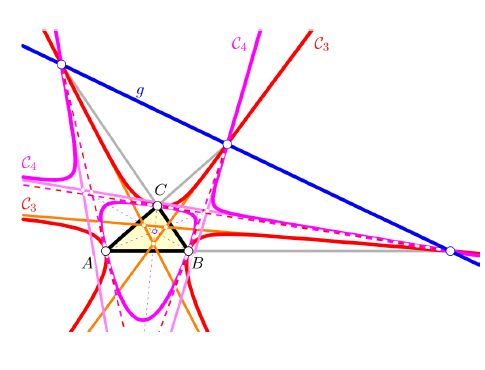
Boris Odehnal (boris.odehnal@uni-ak.ac.at)
Projective Parallelians and Related PorismsWe give a projective generalization of the construction of parallelians and the thus defined conics. To any properly chosen point P and line g in the plane of a triangle Δ = ABC, we construct six points that always lie on a conic P, the parallelian conic P of the pivot P with respect to Δ. Further, we find the parallelian tangent conic T , the parallelian inconic I , and two further conics D and J that are related in a natural way with Δ and P. Any pair out of these conics gives rise to a certain porism and even a chain of porisms by means of polarization. We study the regularity and singularity as well as the relative position of these conics with respect to the line g depending on the choice of P and g. We also give a detailed study of the sets of possible pivot points changing the triangle or hexagon porisms of any pair of conics into such with one-parameter families of quadrangles and pentagons. Key words:
parallelian, parallelian conic, porism, triangle
cubic, triangle center, algebraic transformation |
|
|
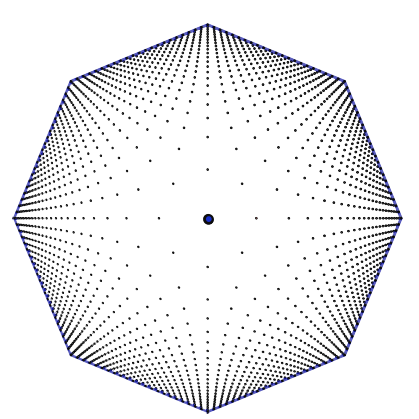
Iva Kodrnja (iva.kodrnja@geof.unizg.hr)
On Remarkable Properties of Number 2025In this paper we investigate the number 2025 and visualize its regularity. This is a perfect square, but a deeper look reveals much more structure related to counting lattice points in polygons and polyhedra. We will also discuss the frequency of square and regular years and the uniqueness of such a regular year number. Key words:
figure numbers, trigonal numbers, tetrahedral
numbers |