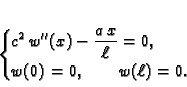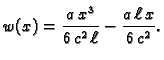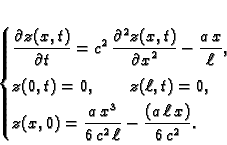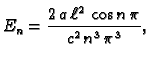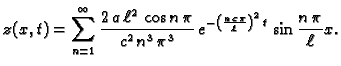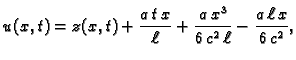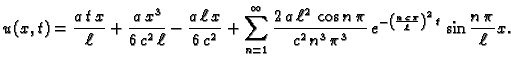



Next: Varijacijske metode
Up: Rubni problemi
Previous: Rubni problemi
Contents
Index
Subsections
Fourierova metoda ili metoda separacije varijabli
Vlastite funkcije i vlastite vrijednosti
Valna jednadžba
opisuje
oscilacije žice, longitudinalne oscilacije štapa i torzijske
oscilacije štapa. Pretpostavimo da ne djeluje vanjska sila,
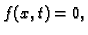 da su
da su 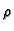 i
i 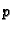 konstante, i neka su zadani homogeni rubni
uvjeti.
konstante, i neka su zadani homogeni rubni
uvjeti.
![\begin{displaymath}
% latex2html id marker 34625
\begin{cases}\frac{\textstyle{\...
...^2}},& \\ [3mm] u(0,t)=0,\hspace{1cm} u(\ell,t)=0, \end{cases}\end{displaymath}](img1484.gif) |
(2.17) |
gdje je
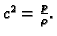 Budući da su oscilacije u
pravilu periodična gibanja u odnosu na vrijeme, potražimo
rješenja ovog rubnog
problema u obliku
Budući da su oscilacije u
pravilu periodična gibanja u odnosu na vrijeme, potražimo
rješenja ovog rubnog
problema u obliku
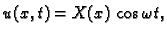
ili
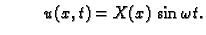
Imamo
dok je
Uvrstimo u jednadžbu
i ako uzmemo u obzir rubne uvjete
dobivamo sljedeći rubni problem za običnu diferencijalnu jednadžbu
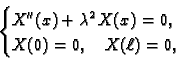 |
(2.18) |
gdje je
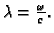 Ovo
je obična linearna homogena diferencijalna jednadžba 2. reda.
Njezina karakteristična jednadžba je
pa je opće rješenje
odakle, pomoću Eulerove formule
dobivamo opće rješenje
Iz
Ovo
je obična linearna homogena diferencijalna jednadžba 2. reda.
Njezina karakteristična jednadžba je
pa je opće rješenje
odakle, pomoću Eulerove formule
dobivamo opće rješenje
Iz 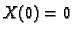 slijedi
slijedi 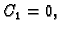 pa je
Iz
pa je
Iz 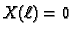 slijedi
Dakle imamo zapravo diskretan skup vrijednosti za
slijedi
Dakle imamo zapravo diskretan skup vrijednosti za 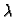 Za
Za 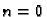 dobivamo trivijalno rješenje (nulfunkciju), a negativni
dobivamo trivijalno rješenje (nulfunkciju), a negativni
 -ovi ne daju ništa novo, jer je sinus neparna funkcija. Tako imamo
Brojevi
-ovi ne daju ništa novo, jer je sinus neparna funkcija. Tako imamo
Brojevi
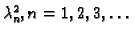 se zovu vlastite
vrijednosti, a pripadne funkcije
se zovu vlastite funkcije rubnog problema
(2.18).
se zovu vlastite
vrijednosti, a pripadne funkcije
se zovu vlastite funkcije rubnog problema
(2.18).
Tako rješenja problema (2.17) imaju oblik
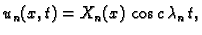
ili
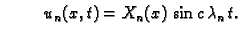
Primjer 2.10
Naći vlastite vrijednosti i vlastite funkcije rubnog problema
Rješenje. Kao u (2.18) opće rješenje jednadžbe je
Iz
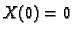
slijedi
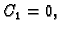
pa je
Iz
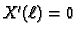
slijedi
Odatle
pa je
Tako su vlastite vrijednosti
Vlastite funkcije su
Primjer 2.11
Naći vlastite vrijednosti i vlastite funkcije rubnog problema
Rješenje. Opće rješenje jednadžbe je
Iz
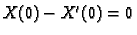
slijedi
Iz
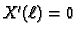
slijedi
odnosno
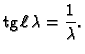 |
(2.19) |
To je transcendentna (nije algebarska) jednadžba. Takve se jednadžbe
u pravilu ne mogu elementarno rješavati, i gotovo uvijek se moramo
zadovoljiti s približnim rješenjem. O približnom rješavanju
jednadžbi bit će riječi u trećem poglavlju
3.2. Ovdje
napomenimo samo toliko da za
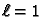
imamo približno
Slika:
Rješenja jednadžbe
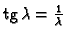
Tako su približne vlastite funkcije
Slika 2.7:
Vlastite funkcije
Fourierovi redovi
Rješavajući valnu jednadžbu, uvaživši rubne uvjete, dobili smo
rješenja oblika
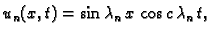
ili
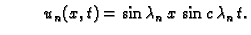
Problem oscilacija žice je
potpuno zadan tek kad zadamo još i početne uvjete. Na pr.
Općenito niti
jedna od funkcija  ne zadovoljava početne uvjete. Zato rješenje
tražimo u obliku linearne kombinacije. Funkcije su linearno
nezavisne, i ima ih beskonačno mnogo, pa linearna kombinacija postaje
beskonačni red
Ako je
ne zadovoljava početne uvjete. Zato rješenje
tražimo u obliku linearne kombinacije. Funkcije su linearno
nezavisne, i ima ih beskonačno mnogo, pa linearna kombinacija postaje
beskonačni red
Ako je  rješenje koje zadovoljava početne uvjete, onda mora biti
Da li postoje takvi
rješenje koje zadovoljava početne uvjete, onda mora biti
Da li postoje takvi  da vrijedi ova jednakost? Za kakve funkcije
postoje
da vrijedi ova jednakost? Za kakve funkcije
postoje 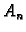 takvi da vrijedi ova jednakost? Ovakva pitanja i još
mnoga druga dovode nas do pojma Fourierovih redova.
takvi da vrijedi ova jednakost? Ovakva pitanja i još
mnoga druga dovode nas do pojma Fourierovih redova.
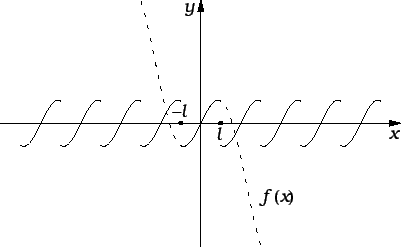
Funkcije
su periodične, i period je broj 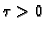 takav da vrijedi
Odatle slijedi
takav da vrijedi
Odatle slijedi
Svaka od ovih funkcija ima period 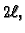 jer je višekratnik perioda
također period, pa se nadamo da pomoću
njih možemo prikazati svaku periodičku funkciju
jer je višekratnik perioda
također period, pa se nadamo da pomoću
njih možemo prikazati svaku periodičku funkciju 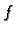 perioda
perioda 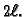 No, pomoću njih se mogu prikazati samo neparne funkcije, jer je
No, pomoću njih se mogu prikazati samo neparne funkcije, jer je
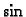 neparna funkcija. To ograničenje izbjegavamo tako da dodamo i
odgovarajuće kosinusne funkcije. Uz
tu pretpostavku imamo
neparna funkcija. To ograničenje izbjegavamo tako da dodamo i
odgovarajuće kosinusne funkcije. Uz
tu pretpostavku imamo
tj.
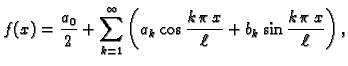 |
(2.20) |
gdje su koeficijenti
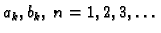 neodređeni. Da bismo
koeficijente odredili tako da vrijedi ova jednakost, koristimo jedno
važno svojstvo trigonometrijskih funkcija
Svojstvo izraženo formulama, u kojima je desna strana jednaka nuli,
se zove ortogonalnost trigonometrijskih
funkcija, a formule se zovu formule
ortogonalnosti.
neodređeni. Da bismo
koeficijente odredili tako da vrijedi ova jednakost, koristimo jedno
važno svojstvo trigonometrijskih funkcija
Svojstvo izraženo formulama, u kojima je desna strana jednaka nuli,
se zove ortogonalnost trigonometrijskih
funkcija, a formule se zovu formule
ortogonalnosti.
Sada računamo koeficijente tako da (2.20) množimo redom
s
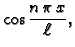
i
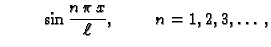
i zatim integriramo po
segmentu duljine perioda, na pr.
![$ [-\ell,\ell].$](img1555.gif) Zbog svojstva
ortogonalnosti dobivamo
Da bi ove formule imale smisla, nužno je da
Zbog svojstva
ortogonalnosti dobivamo
Da bi ove formule imale smisla, nužno je da 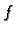 bude integrabilna
funkcija na segmentu
bude integrabilna
funkcija na segmentu
![$ [-\ell,\ell].$](img1555.gif) U tom slučaju su koeficijenti
U tom slučaju su koeficijenti
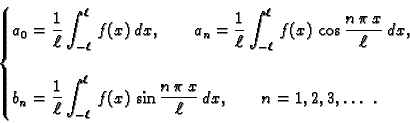 |
(2.21) |
Red oblika
se zove trigonometrijski red, a brojevi
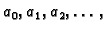
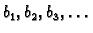 se zovu koeficijenti trigonometrijskog
reda. Trigonometrijski red je dan čim su dani njegovi
koeficijenti. No, ako su koeficijenti trigonometrijskog reda dani
formulama (2.21), onda se red zove Fourierov red
funkcije
se zovu koeficijenti trigonometrijskog
reda. Trigonometrijski red je dan čim su dani njegovi
koeficijenti. No, ako su koeficijenti trigonometrijskog reda dani
formulama (2.21), onda se red zove Fourierov red
funkcije 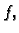 a koeficijenti se zovu
Fourierovi koeficijenti.
a koeficijenti se zovu
Fourierovi koeficijenti.
Do sada smo stalno imali na umu periodičku funkciju 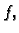 perioda
perioda
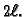 Pretpostavimo da je funkcija
Pretpostavimo da je funkcija 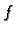 definirana na skupu koji
sadrži
definirana na skupu koji
sadrži
![$ [-\ell,\ell],$](img1563.gif) da je integrabilna na
da je integrabilna na
![$ [-\ell,\ell],$](img1563.gif) i da
nije periodička. U tom slučaju također možemo izračunati
Fourierove koeficijente i prema tome imamo Fourierov red. Budući da
svaka funkcija u tom redu ima period
i da
nije periodička. U tom slučaju također možemo izračunati
Fourierove koeficijente i prema tome imamo Fourierov red. Budući da
svaka funkcija u tom redu ima period 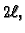 i red će predstavljati
periodičku funkciju perioda
i red će predstavljati
periodičku funkciju perioda 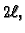 i to onu koja se iz dane dobije
periodičkim proširenjem njezine restrikcije na segmentu
i to onu koja se iz dane dobije
periodičkim proširenjem njezine restrikcije na segmentu
![$ [-\ell,\ell]$](img1564.gif) na cijeli
na cijeli 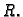 Reći ćemo da je to red funkcije
Reći ćemo da je to red funkcije 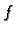 na
na
![$ [-\ell,\ell].$](img1555.gif)
Konvergencija.
Detaljnije o tome, a i o Fourierovim redovima općenito v. [8]. Problemi konvergencije Fourierovih redova su vrlo složeni. Posebno je to zbog toga što smo kod računanja Fourierovih koeficijenata
funkcije 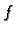 integralom ulazili pod beskonačnu sumu, što je
općenito nedopustiva operacija. Istaknimo ovdje da, ako je
funkcija
integralom ulazili pod beskonačnu sumu, što je
općenito nedopustiva operacija. Istaknimo ovdje da, ako je
funkcija 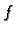 neprekidna, onda njezin Fouriereov red konvergira u
svakoj točki iz
neprekidna, onda njezin Fouriereov red konvergira u
svakoj točki iz
![$ [-\ell,\ell]$](img1564.gif) i to k vrijednosti funkcije u toj
točki, pa za takvu funkciju doista možemo pisati
i to k vrijednosti funkcije u toj
točki, pa za takvu funkciju doista možemo pisati
Slika 2.8:
Grafovi prvih deset parcijalnih suma Fourierovog reda funkcije 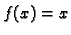 na intervalu
na intervalu
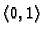
Ako funkcija ima prekid prve vrste u
![$ x_0\in [-\ell,\ell],$](img1570.gif) tj. ako
postoje limesi s lijeva i s desna ali nisu jednaki, onda njezin
Fourierov red konvergira k aritmetičkoj sredini limesa s lijeva i
limesa s desna
tj. ako
postoje limesi s lijeva i s desna ali nisu jednaki, onda njezin
Fourierov red konvergira k aritmetičkoj sredini limesa s lijeva i
limesa s desna
Isto tako se ponaša Fourierov red na rubovima, ako se prilikom
proširenja po periodičnosti dogodi skok prve vrste na rubovima.
Primjer 2.12
Nađimo Fourierov red funkcije
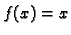
na intervalu
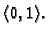 Rješenje
Rješenje. Potrebno je izračunati Fourierove koeficijente po formulama
(
2.21). Period je
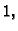
pa bismo trebali integrirati od
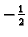
do
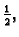
ali ne ovu funkciju, već onu, koja
se iz ove dobije proširenjem po periodičnosti (nacrtajte
periodičko proširenje!). To bi bilo
nespretno, jer se proširenje ne može opisati jednom formulom. Iz
periodičnosti slijedi, da prilikom integracije nisu bitne donja i
gornja granica, već samo duljina područja integracije. Zato
integriramo od 0 do
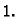
pa je tako Fourierov red
Neparne i parne funkcije.
Ako je 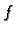 neparna funkcija, onda je
neparna funkcija, onda je
pa je
Također
pa je na sličan način
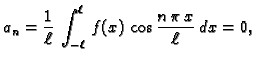
za
Tako Fourierov red
neparne funkcije sadrži samo sinuse
Vrijedi i obrat. U ovom redu je svaki član
neparna funkcija, pa ako ovaj red predstavlja neku funkciju, onda je ona
također neparna.
Osim toga
pa je
Slično bismo u slučaju parnosti funkcije dobili  pa je Fourierov red takve funkcije oblika
pa je Fourierov red takve funkcije oblika
s tim da je
Primjer 2.13
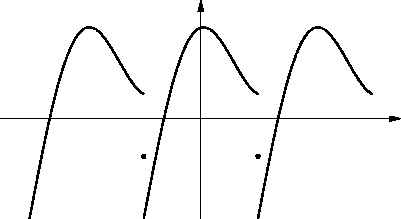
Treba naći Fourierov red po kosinusima funkcije
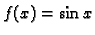
na
intervalu
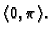 Rješenje
Rješenje. Tu se radi o proširenju po parnosti prvog brijega sinusne
funkcije. Period je
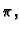
pa su Fourierovi koeficijenti
Za
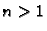
dok je
Tako je Fourierov red
Primjer 2.14
Naći Fourierov red funkcije
na segmentu
![$ [-\pi,\pi].$](img1601.gif)
Rješenje. Svaki sumand od 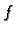 je potencija ili produkt potencija
trigonometrijskih funkcija perioda
je potencija ili produkt potencija
trigonometrijskih funkcija perioda 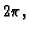 što
je upravo duljina segmenta na kojem želimo napisati Fourierov red. U
tom slučaju je dovoljno svaki od sumanada napisati pomoću linearne
kombinacije trigonometrijskih funkcija višestrukog srgumenta.
što
je upravo duljina segmenta na kojem želimo napisati Fourierov red. U
tom slučaju je dovoljno svaki od sumanada napisati pomoću linearne
kombinacije trigonometrijskih funkcija višestrukog srgumenta.
Odatle
Dakle
a ostali Fourierovi koeficijenti su jednaki nuli.
Slobodne oscilacije žice
Pod slobodnim oscilacijama žice podrazumijevamo oscilacije, koje nastaju
uslijed početnih uvjeta, a bez utjecaja vanjske sile. Tako je
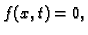 pa imamo sljedeći rubno-početni problem
pa imamo sljedeći rubno-početni problem
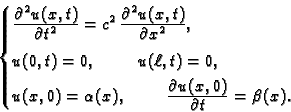 |
(2.22) |
Pretpostavimo rješenje u obliku funkcije
Ova pretpostavka je ključna za metodu koju
ćemo sada opisati, a zove se Fourierova metoda ili
metoda separacije varijabli. Uz ovu pretpostavku jednadžba
postaje
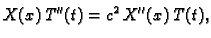 |
(2.23) |
a rubni uvjeti
odakle slijedi
jer
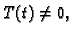 za barem jedan
za barem jedan 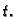 U protivnom bismo imali
U protivnom bismo imali
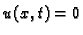 za svaki
za svaki 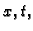 pa bi žica mirovala, što nije moguće
ako je početnim uvjetima izvučena iz položaja ravnoteže.
pa bi žica mirovala, što nije moguće
ako je početnim uvjetima izvučena iz položaja ravnoteže.
U jednadžbi (2.23) možemo separirati varijable dijeleći je s
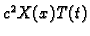
Lijeva
strana ove jednadžbe ovisi samo o 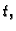 a desna samo o
a desna samo o 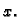 Kako su
varijable
Kako su
varijable 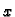 i
i 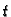 nezavisne, slijedi
gdje
je
nezavisne, slijedi
gdje
je 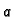 konstanta. Tako imamo sljedeći rubni problem
Pomnožimo ovu jednadžbu s
konstanta. Tako imamo sljedeći rubni problem
Pomnožimo ovu jednadžbu s 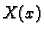 i integrirajmo po
i integrirajmo po 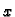 po segmentu
po segmentu
![$ [0,\ell].$](img1625.gif) Parcijalno
integrirajmo integral na lijevoj strani, i uvrstimo rubne uvjete
pa je
Odavde slijedi da je
Parcijalno
integrirajmo integral na lijevoj strani, i uvrstimo rubne uvjete
pa je
Odavde slijedi da je 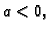 pa
možemo staviti
pa
možemo staviti
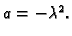 Tako imamo rubni problem
Tako imamo rubni problem
 |
(2.24) |
Ovaj problem smo već riješili u 2.3.1, i dobili
Za svaki
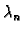 imamo po jednu jednadžbu za
imamo po jednu jednadžbu za 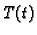 pa je opće
rješenje
odnosno
Tako imamo niz rješenja
međutim nijedno od njih, u općem slučaju, ne
zadovoljava početne uvjete. Općenito će tek beskonačni red
pa je opće
rješenje
odnosno
Tako imamo niz rješenja
međutim nijedno od njih, u općem slučaju, ne
zadovoljava početne uvjete. Općenito će tek beskonačni red
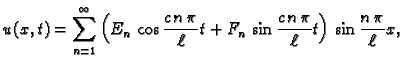 |
(2.25) |
zadovoljiti početni uvjet. Ovdje su 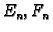 neodređeni
koeficijenti, koje određujemo pomoću početnih uvjeta.
Suma u ovoj formuli je
Fourierov red neparne funkcije definirane na segmentu
neodređeni
koeficijenti, koje određujemo pomoću početnih uvjeta.
Suma u ovoj formuli je
Fourierov red neparne funkcije definirane na segmentu
![$ [-\ell,\ell].$](img1555.gif) Budući da se na
Budući da se na ![$ [0,\ell{}]$](img1456.gif) podudara s funkcijom
podudara s funkcijom
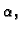 to znači da je to Fourierov red funkcije koja je iz
to znači da je to Fourierov red funkcije koja je iz
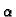 dobivena proširenjem po neparnosti s
dobivena proširenjem po neparnosti s ![$ [0,\ell{}]$](img1456.gif) na
na
![$ [-\ell,\ell].$](img1555.gif) Tako je
Iskoristimo i drugi početni uvjet
Kao gore
imamo
odnosno
Tako je
Iskoristimo i drugi početni uvjet
Kao gore
imamo
odnosno
Iz ovog razmatranja vidimo da je za upotrebu Fourierove metode nužno
imati početne uvjete koji se mogu razložiti u Fourierov red.
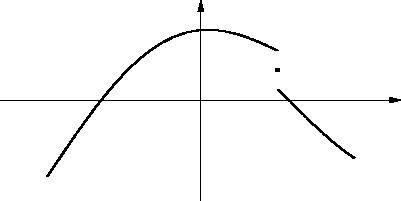
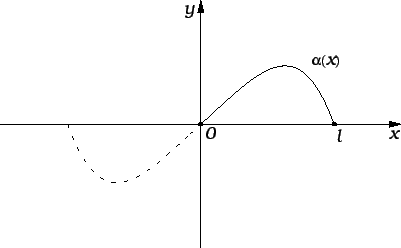
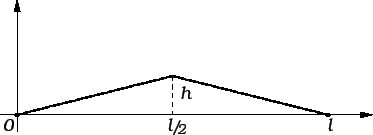
Primjer 2.15
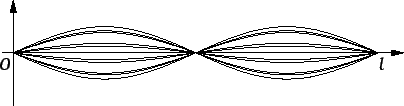
Naći slobodne oscilacije napete homogene žice, duljine
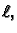
učvršćene na rubovima, ako je početna brzina jednaka nuli, a
početni pomak kao na slici.
Rješenje. Budući da nema vanjske sile, i da su uvjeti na rubu homogeni,
vlastite vrijednosti i vlastite funkcije su kao u rubnom problemu
(2.22). Vidjeli smo da se u tom slučaju rješenje
može pretpostaviti u obliku (2.25). Pri tom su nepoznati
koeficijenti 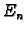 Fourierovi koeficijenti početnog pomaka, a
Fourierovi koeficijenti početnog pomaka, a 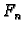 su, do na faktor, Fourierovi koeficijenti početne brzine. Kako je
početna brzina
su, do na faktor, Fourierovi koeficijenti početne brzine. Kako je
početna brzina 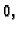 slijedi
slijedi 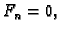 za
za
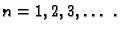 Ostaje
izračunati
Ostaje
izračunati 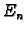 po formuli
po formuli
Tako su koeficijenti
pa je rješenje
Interpretacija rješenja.
Budući da je
postoji 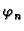 takav da je
pa je
Tako je
takav da je
pa je
Tako je
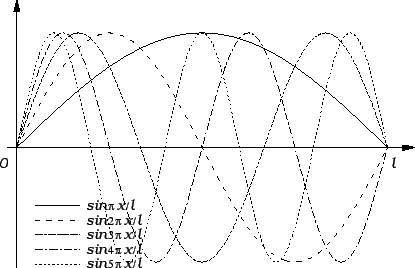
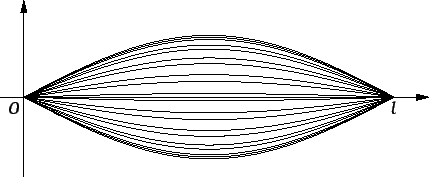
Za 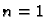 imamo
imamo
U odnosu na varijablu 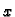 ova funkcija ima temeljni period
To znači da rubne točke
ova funkcija ima temeljni period
To znači da rubne točke 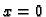 i
i 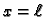 miruju, i zbog toga se zovu
čvorovi, a ostale se gibaju
sinkrono s frekvencijom
i s amplitudom
miruju, i zbog toga se zovu
čvorovi, a ostale se gibaju
sinkrono s frekvencijom
i s amplitudom
Za 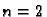 imamo
imamo
U odnosu na varijablu 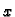 ova funkcija ima temeljni period
To znači da su sada čvorovi točke
ova funkcija ima temeljni period
To znači da su sada čvorovi točke 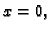
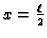 i
i
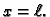 Ostale se gibaju sinkrono s frekvencijom
i s amplitudom
Ostale se gibaju sinkrono s frekvencijom
i s amplitudom
Za 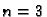 imamo čvorove
imamo čvorove
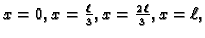 frekvencija
titranja je
frekvencija
titranja je
itd.
Ovakva titranja se zovu stojni
valovi.
Stvarno slobodno titranje je superpozicija ovakvih titranja. Kad se
radi o napetoj žici, ona prilikom titranja proizvodi ton. Broj
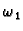 se zove frekvencija osnovnog tona, a ostale
frekvencije se zovu frekvencije viših
harmonika. Amplitude
viših harmonika vrlo brzo opadaju prema nuli. Njihova distribucija
daje boju proizvedenom tonu. Primijetimo na kraju da je frekvencija
osnovnog tona
se zove frekvencija osnovnog tona, a ostale
frekvencije se zovu frekvencije viših
harmonika. Amplitude
viših harmonika vrlo brzo opadaju prema nuli. Njihova distribucija
daje boju proizvedenom tonu. Primijetimo na kraju da je frekvencija
osnovnog tona
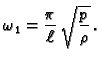
Primjer 2.16
Naći oscilacije napete homogene žice, duljine
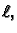
učvršćene na rubovima, u sredstvu s otporom proporcionalnim
brzini, ako su početni uvjeti kao u primjeru
2.15.
Rješenje. Rubni i početni uvjeti su kao u primjeru 2.15, a
jednadžba glasi
Stavimo
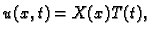
i podijelimo s
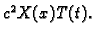
Dobivamo
Varijable su separirane, pa je svaka strana ove jednakosti
konstanta. Kao i ranije zaključujemo da je ta konstanta negativna, i
da su vlastite vrijednosti
i vlastite funkcije
Vremenska jednadžba sada glasi
Ovo je obična linearna diferencijalna jednadžba drugog reda s
konstantnim koeficijentima. Pretpostavka
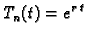
vodi na
karakterističnu jednadžbu
Rješenja su
Ako je
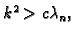
tj. ako je otpor dovoljno velik, onda nema
osciliranja. Pretpostavimo da je otpor dovoljno malen tako da je
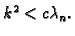
Tada je
Tako je
što se pomoću Eulerove formule može napisati kao
Stavimo
Tada je rješenje oblika
Koeficijenti
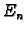
i
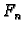
se računaju kao i u primjeru
2.15.
Faktor
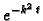 teži k nuli kad
teži k nuli kad
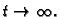 Zato titranje postaje sve slabije kako
Zato titranje postaje sve slabije kako 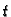 raste. Tako imamo prigušene oscilacije.
raste. Tako imamo prigušene oscilacije.
Homogenizacija rubnih uvjeta.
Želimo riješiti problem slobodnih oscilacija žice uz zadane nehomogene rubne uvjete.
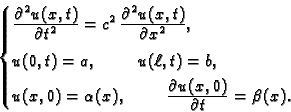 |
(2.26) |
Najprije homogeniziramo rubne uvjete kao u 2.3.3. Na taj način homogeniziramo rubne uvjete, ali se pojavi nehomogena diferencijalna jednadžba
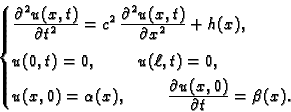 |
(2.27) |
Sada homogeniziramo jednadžbu na sljedeći način.
Rješenje pretpostavljamo u obliku
gdje je 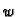 rješenje stacionarnog rubnog problema
Uvrstimo
rješenje stacionarnog rubnog problema
Uvrstimo 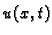 u jednadžbu. Budući da
u jednadžbu. Budući da 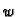 ne ovisi o
ne ovisi o 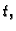 imamo
jer je
imamo
jer je
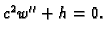
Rubni uvjeti ostaju isti, a početni uvjeti se mijenjaju
pa je tako početni položaj
a početna brzina ostaje
jer
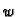 ne ovisi o
ne ovisi o 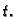 Tako smo problem sveli na homogenu jednadžbu i
homogene rubne uvjete, što smo već riješili.
Tako smo problem sveli na homogenu jednadžbu i
homogene rubne uvjete, što smo već riješili.
Prisilne oscilacije
Ako je zadana vanjska sila po jedinici duljine 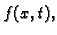 onda treba
riješiti sljedeći rubni problem
onda treba
riješiti sljedeći rubni problem
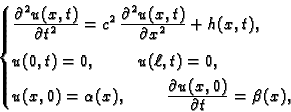 |
(2.28) |
gdje je
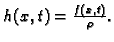
Uzimajući u obzir rezultate prethodne točke, 2.3.3,
rješenje (2.28) možemo pretpostaviti u obliku
Ovom formom rješenja pretpostavljamo da se rješenje može razviti u
red po vlastitim funkcijama rubnog problema. Neodređene funkcije
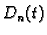 određujemo pomoću jednadžbe i početnih uvjeta. Kad
uvrstimo
određujemo pomoću jednadžbe i početnih uvjeta. Kad
uvrstimo 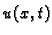 u jednadžbu, dobivamo
odnosno
Za svaki
u jednadžbu, dobivamo
odnosno
Za svaki 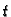 ovo je Fourierov
red po sinusima za funkciju
ovo je Fourierov
red po sinusima za funkciju 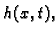 shvaćenu kao funkciju od
shvaćenu kao funkciju od 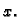 Neka je
gdje je
Slijedi
Nadalje
pa je
Analogno
pa je
Tako imamo familiju
diferencijalnih jednadžbi s početnim uvjetima
i svaka daje jedno
rješenje
Neka je
gdje je
Slijedi
Nadalje
pa je
Analogno
pa je
Tako imamo familiju
diferencijalnih jednadžbi s početnim uvjetima
i svaka daje jedno
rješenje 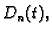 što zatim uvrstimo u formulu za
što zatim uvrstimo u formulu za 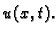
Primjer 2.17
Riješiti rubno-početni problem
Rješenje. Imamo
Dakle diferencijalne jednadžbe za koeficijent
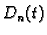
glase
Budući da su početni uvjeti homogeni, početni uvjeti za ovu
familiju diferencijalnih jednadžbi su također homogeni
Rješenja su
pa je rješenje problema
Provođenje topline kroz štap
Neka su 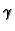 i
i 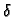 (v. 2.1.4) konstante, i
neka je
(v. 2.1.4) konstante, i
neka je
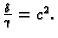 Tada je rubno-početni problem
provođenja zadan kako slijedi
Tada je rubno-početni problem
provođenja zadan kako slijedi
![\begin{displaymath}
% latex2html id marker 35297
\begin{cases}\frac{\textstyle{\...
...\hspace{1cm} u(\ell,t)=0,& \\ [1mm] u(x,0) = g(x). \end{cases}\end{displaymath}](img1741.gif) |
(2.29) |
Rješenje tražimo u obliku
Uz ovu
pretpostavku jednadžba postaje
Podijelimo s
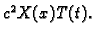 Dobivamo
Negativnost ove konstante se dokazuje kao kod valne
jednadžbe (v. 2.3.3). Na isti način kao kod valne
jednadžbe iz rubnih uvjeta dobivamo
Dobivamo
Negativnost ove konstante se dokazuje kao kod valne
jednadžbe (v. 2.3.3). Na isti način kao kod valne
jednadžbe iz rubnih uvjeta dobivamo
S druge strane
Rješenje ove
jednadžbe je
Tako je
Ove funkcije rješavaju jednadžbu, i
zadovoljavaju rubne uvjete. No da bi bio zadovoljen i početni uvjet,
treba rješenje pretpostaviti u obliku beskonačnog reda (v. 2.3.3)
Početni uvjet daje
Dakle
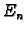 su Fourierovi koeficijenti funkcije
su Fourierovi koeficijenti funkcije 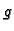 proširene po neparnosti
s
proširene po neparnosti
s ![$ [0,\ell{}]$](img1456.gif) na
na
![$ [-\ell,\ell].$](img1555.gif) Tako je
Neka je jednadžba nehomogena
gdje je
Tako je
Neka je jednadžba nehomogena
gdje je 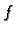 toplina po jedinici duljine podijeljena s
toplinskim kapacitetom jedinice duljine štapa
toplina po jedinici duljine podijeljena s
toplinskim kapacitetom jedinice duljine štapa 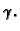 Uz iste rubne
i početne uvjete rješenje pretpostavljamo u obliku
Neodređene koeficijente
Uz iste rubne
i početne uvjete rješenje pretpostavljamo u obliku
Neodređene koeficijente 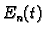 ćemo odrediti tako da
ćemo odrediti tako da  zadovoljava jednadžbu i početni uvjet.
odnosno
Lijeva strana je Fourierov
red, ako
zadovoljava jednadžbu i početni uvjet.
odnosno
Lijeva strana je Fourierov
red, ako 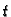 shvatimo kao parametar. Pretpostavimo da je
gdje je
Slijedi
Početni uvjet nam daje
tj.
Tako smo dobili familiju diferencijalnih jednadžbi s pripadnim
početnim uvjetima, čija rješenja daju neodređene koeficijente.
shvatimo kao parametar. Pretpostavimo da je
gdje je
Slijedi
Početni uvjet nam daje
tj.
Tako smo dobili familiju diferencijalnih jednadžbi s pripadnim
početnim uvjetima, čija rješenja daju neodređene koeficijente.
Primjer 2.18
Naći raspodjelu temperature u homogenom tankom štapu, duljine
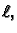
bočno toplinski izoliranom, ako se na lijevom kraju
održava temperatura
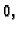
a na desnom se mijenja s vremenom po
formuli
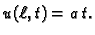
Početna temperatura štapa je
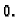
Rješenje. Rubno-početni problem glasi
Najprije treba homogenizirati rubne uvjete. Očito funkcija
zadovoljava homogene rubne
uvjete. Pripadni rubno-početni problem za
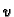
je
Sada homogeniziramo jednadžbu. Stavimo
gdje je
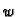
rješenje problema
Rješenje ovog problema je
Na taj način smo
homogenizirali rubne uvjete i jednadžbu, ali se nehomogenost pojavila
u početnom uvjetu. Tako
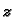
rješava sljedeći rubno-početni problem
pa je rješenje rubnog problema za
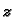
Rješenje početnog problema je
dakle




Next: Varijacijske metode
Up: Rubni problemi
Previous: Rubni problemi
Contents
Index
Salih Suljagic
1999-12-17
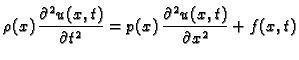
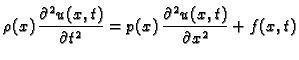
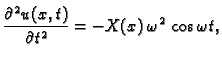
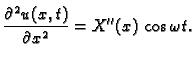
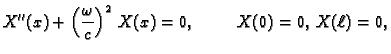
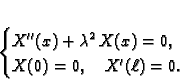
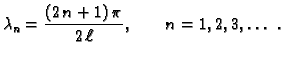
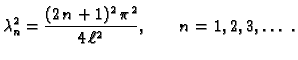
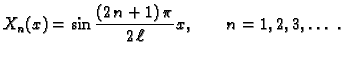
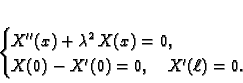
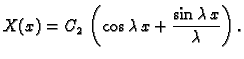
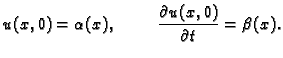
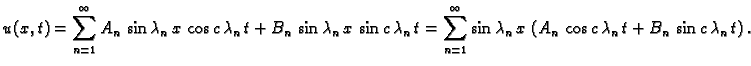
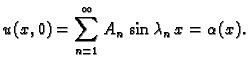
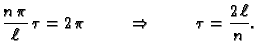
![]() jer je višekratnik perioda
također period, pa se nadamo da pomoću
njih možemo prikazati svaku periodičku funkciju
jer je višekratnik perioda
također period, pa se nadamo da pomoću
njih možemo prikazati svaku periodičku funkciju ![]() perioda
perioda ![]() No, pomoću njih se mogu prikazati samo neparne funkcije, jer je
No, pomoću njih se mogu prikazati samo neparne funkcije, jer je
![]() neparna funkcija. To ograničenje izbjegavamo tako da dodamo i
odgovarajuće kosinusne funkcije. Uz
tu pretpostavku imamo
neparna funkcija. To ograničenje izbjegavamo tako da dodamo i
odgovarajuće kosinusne funkcije. Uz
tu pretpostavku imamo
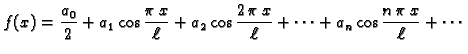
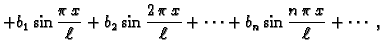
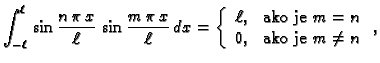
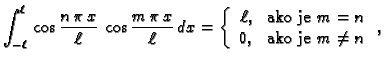
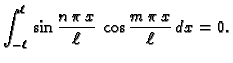
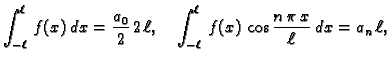
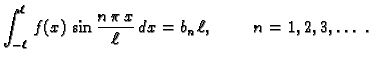
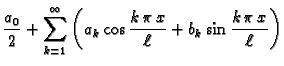
![]() perioda
perioda
![]() Pretpostavimo da je funkcija
Pretpostavimo da je funkcija ![]() definirana na skupu koji
sadrži
definirana na skupu koji
sadrži
![]() da je integrabilna na
da je integrabilna na
![]() i da
nije periodička. U tom slučaju također možemo izračunati
Fourierove koeficijente i prema tome imamo Fourierov red. Budući da
svaka funkcija u tom redu ima period
i da
nije periodička. U tom slučaju također možemo izračunati
Fourierove koeficijente i prema tome imamo Fourierov red. Budući da
svaka funkcija u tom redu ima period ![]() i red će predstavljati
periodičku funkciju perioda
i red će predstavljati
periodičku funkciju perioda ![]() i to onu koja se iz dane dobije
periodičkim proširenjem njezine restrikcije na segmentu
i to onu koja se iz dane dobije
periodičkim proširenjem njezine restrikcije na segmentu
![]() na cijeli
na cijeli ![]() Reći ćemo da je to red funkcije
Reći ćemo da je to red funkcije ![]() na
na
![]()
![]() integralom ulazili pod beskonačnu sumu, što je
općenito nedopustiva operacija. Istaknimo ovdje da, ako je
funkcija
integralom ulazili pod beskonačnu sumu, što je
općenito nedopustiva operacija. Istaknimo ovdje da, ako je
funkcija ![]() neprekidna, onda njezin Fouriereov red konvergira u
svakoj točki iz
neprekidna, onda njezin Fouriereov red konvergira u
svakoj točki iz
![]() i to k vrijednosti funkcije u toj
točki, pa za takvu funkciju doista možemo pisati
i to k vrijednosti funkcije u toj
točki, pa za takvu funkciju doista možemo pisati
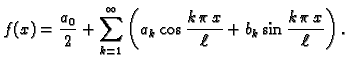
![]() tj. ako
postoje limesi s lijeva i s desna ali nisu jednaki, onda njezin
Fourierov red konvergira k aritmetičkoj sredini limesa s lijeva i
limesa s desna
tj. ako
postoje limesi s lijeva i s desna ali nisu jednaki, onda njezin
Fourierov red konvergira k aritmetičkoj sredini limesa s lijeva i
limesa s desna
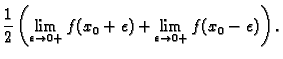
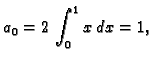
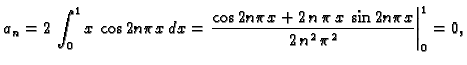
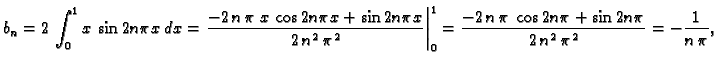
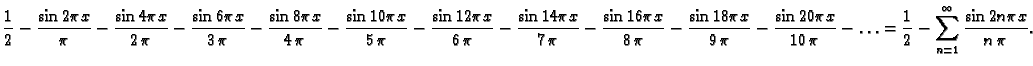
![]() neparna funkcija, onda je
neparna funkcija, onda je
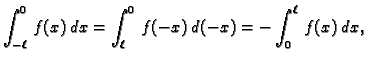
![$\displaystyle a_0 = \frac{1}{\ell}\,\int_{-\ell}^{\ell}\,f(x)\,dx = \frac{1}{\ell}\,\left[\int_{-\ell}^0\,
f(x)\,dx + \int_0^{\ell}\,f(x)\,dx\right] = 0.$](img1582.gif)
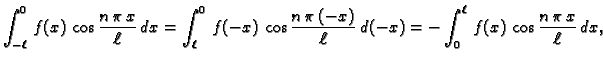
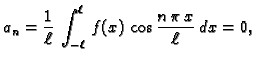 za
za 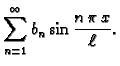
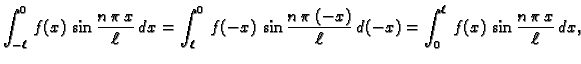
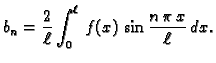
![]() pa je Fourierov red takve funkcije oblika
pa je Fourierov red takve funkcije oblika
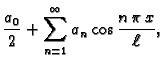
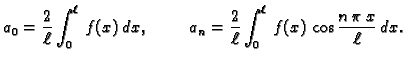
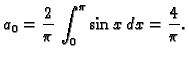
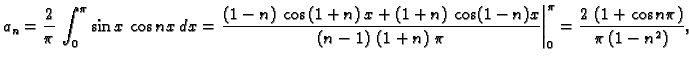
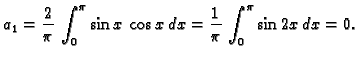
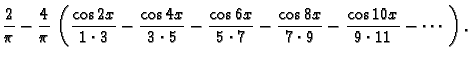
![]() je potencija ili produkt potencija
trigonometrijskih funkcija perioda
je potencija ili produkt potencija
trigonometrijskih funkcija perioda ![]() što
je upravo duljina segmenta na kojem želimo napisati Fourierov red. U
tom slučaju je dovoljno svaki od sumanada napisati pomoću linearne
kombinacije trigonometrijskih funkcija višestrukog srgumenta.
što
je upravo duljina segmenta na kojem želimo napisati Fourierov red. U
tom slučaju je dovoljno svaki od sumanada napisati pomoću linearne
kombinacije trigonometrijskih funkcija višestrukog srgumenta.
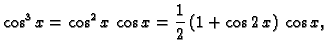
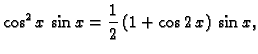
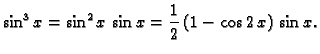
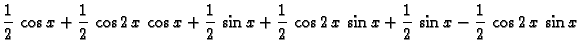
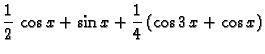
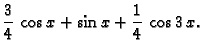
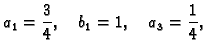
![]() pa imamo sljedeći rubno-početni problem
pa imamo sljedeći rubno-početni problem
![]()
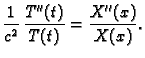
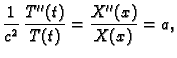
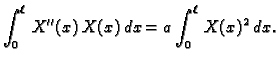
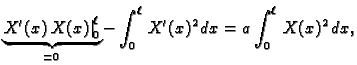
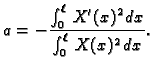
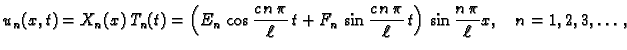
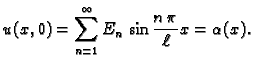
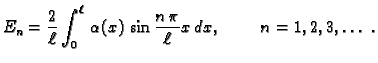
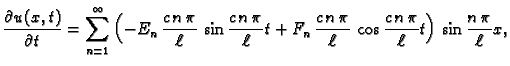
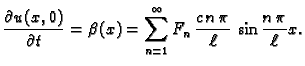
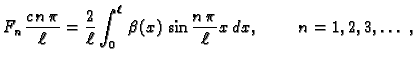
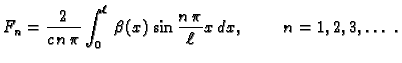
![]() Fourierovi koeficijenti početnog pomaka, a
Fourierovi koeficijenti početnog pomaka, a ![]() su, do na faktor, Fourierovi koeficijenti početne brzine. Kako je
početna brzina
su, do na faktor, Fourierovi koeficijenti početne brzine. Kako je
početna brzina ![]() slijedi
slijedi ![]() za
za
![]() Ostaje
izračunati
Ostaje
izračunati ![]() po formuli
po formuli
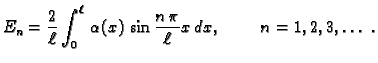
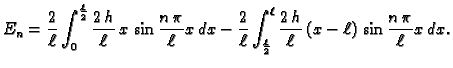
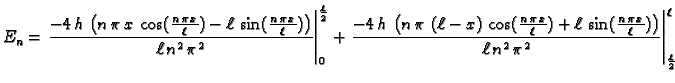
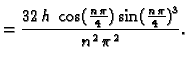
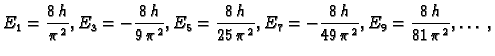
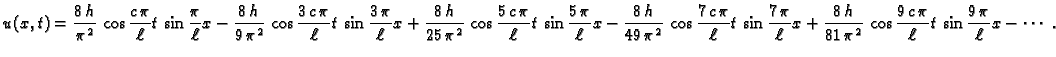
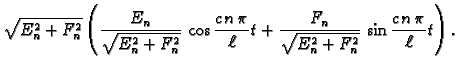
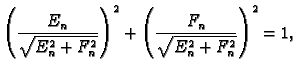
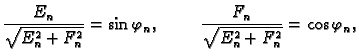
![]() imamo
imamo
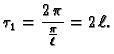
![]() imamo
imamo
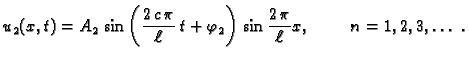
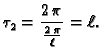
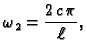
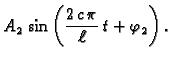
![]() imamo čvorove
imamo čvorove
![]() frekvencija
titranja je
frekvencija
titranja je
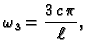

![]() se zove frekvencija osnovnog tona, a ostale
frekvencije se zovu frekvencije viših
harmonika. Amplitude
viših harmonika vrlo brzo opadaju prema nuli. Njihova distribucija
daje boju proizvedenom tonu. Primijetimo na kraju da je frekvencija
osnovnog tona
se zove frekvencija osnovnog tona, a ostale
frekvencije se zovu frekvencije viših
harmonika. Amplitude
viših harmonika vrlo brzo opadaju prema nuli. Njihova distribucija
daje boju proizvedenom tonu. Primijetimo na kraju da je frekvencija
osnovnog tona
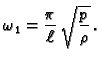
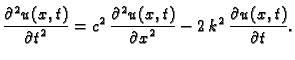
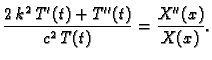
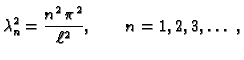
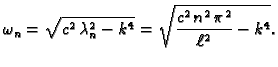
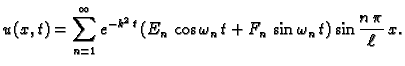
![]() teži k nuli kad
teži k nuli kad
![]() Zato titranje postaje sve slabije kako
Zato titranje postaje sve slabije kako ![]() raste. Tako imamo prigušene oscilacije.
raste. Tako imamo prigušene oscilacije.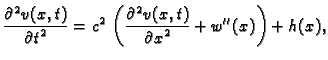
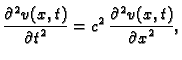
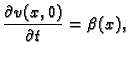
![]() onda treba
riješiti sljedeći rubni problem
onda treba
riješiti sljedeći rubni problem
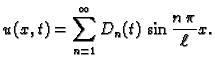
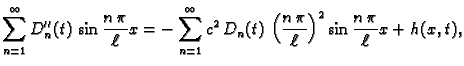
![$\displaystyle \sum_{n=1}^{\infty}
\left[D''_n(t) + \left(c\,\frac{n\,\pi}{\ell}\right)^2D_n(t)\right]
\,\sin\frac{n\,\pi}{\ell}x = h(x,t).$](img1722.gif)
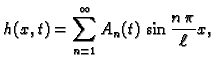
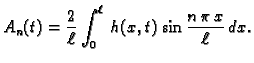
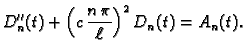
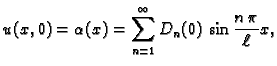
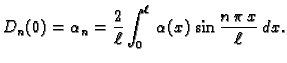
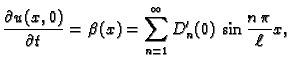
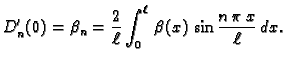
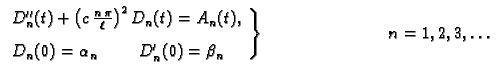
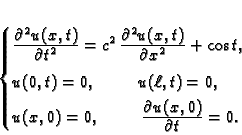
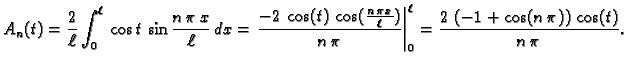
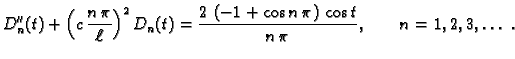
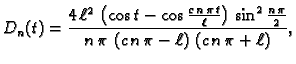
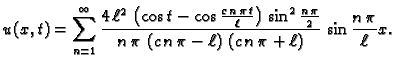
![]() i
i ![]() (v. 2.1.4) konstante, i
neka je
(v. 2.1.4) konstante, i
neka je
![]() Tada je rubno-početni problem
provođenja zadan kako slijedi
Tada je rubno-početni problem
provođenja zadan kako slijedi
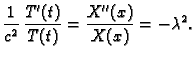
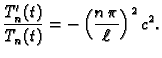
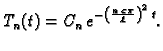
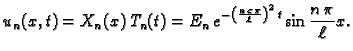
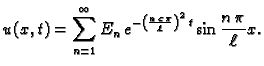
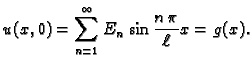
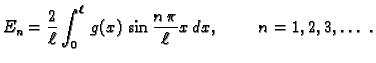
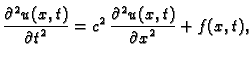
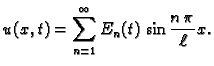
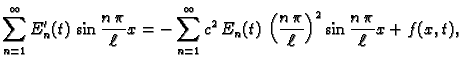
![$\displaystyle \sum_{n=1}^{\infty}
\left[E'_n(t) + \left(c\,\frac{n\,\pi}{\ell}\right)^2E_n(t)\right]
\,\sin\frac{n\,\pi}{\ell}x = f(x,t).$](img1756.gif)
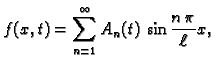
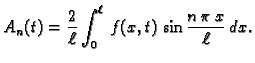
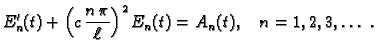
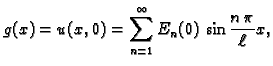
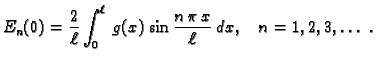
![\begin{displaymath}
% latex2html id marker 35366\begin{cases}
\frac{\textstyle...
...t)=0,\qquad u(\ell,t)=a\,t,& \\ [1mm]
u(x,0) = 0.
\end{cases}\end{displaymath}](img1763.gif)
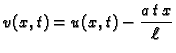
![\begin{displaymath}
% latex2html id marker 35372\begin{cases}
\displaystyle \f...
...(0,t)=0,\qquad v(\ell,t)=0,& \\ [1mm]
v(x,0) = 0.
\end{cases}\end{displaymath}](img1766.gif)