



Next: Fourierova metoda
Up: Rubni problemi
Previous: Jednadžbe
Contents
Index
Subsections
Rubni problemi
Rubni i početni uvjeti
Jednadžbe
koje smo upravo izveli su diferencijalne jednadžbe. Svaka od njih ima
beskonačno mnogo rješenja. Ipak,
u stvarnosti žica zauzme sasvim određen ravnotežni položaj. Isto
tako oscilira na sasvim određen način. To je zbog toga što su u
stvarnosti određeni uvjeti na rubu žice i početni
uvjeti, tj. način na koji je žica izvučena iz položaja
ravnoteže.
Navedimo sada neke jednostavne rubne uvjete.
Kinematički (Dirichletov, geometrijski, prvi) rubni uvjet.
Kinematički rubni uvjet je uvjet koji određuje vrijednost
kinematičkog polja na rubovima, na pr.
 |
(2.4) |
Za rub u kojem je zadan Dirichletov rubni uvjet kažemo da je
učvršćen.
Ako je 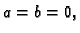 onda kažemo da su rubni uvjeti
homogeni.
onda kažemo da su rubni uvjeti
homogeni.
Dirichletov rubni uvjet znači u slučaju
- a)
- oscilacija ili ravnoteže žice, longitudinalnih oscilacija
grede, torzijskih oscilacija tankog štapa, da su rubovi učvršćeni,
- b)
- provođenja topline, da se rub održava na stalnoj temperaturi,
i to
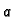 na lijevom rubu,
na lijevom rubu, 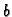 na desnom rubu štapa,
na desnom rubu štapa,
- c)
- filtracije, da su tlakovi na rubovima zadani. Ako su rubni
uvjeti homogeni, onda to znači da tekućina može slobodno
protjecati kroz rub.
Dinamički (Neumannov, prirodni, drugi) rubni uvjet.
Dinamički rubni uvjet je uvjet koji određuje vrijednost
dinamičkog polja 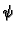 na rubovima, na
pr.
na rubovima, na
pr.
Zakoni ponašanja
povezuju 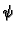 i
i 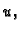 pa se tako i dinamički rubni uvjeti mogu
izraziti pomoću polja
pa se tako i dinamički rubni uvjeti mogu
izraziti pomoću polja 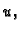 ali preko njegovih derivacija. Za žicu
smo imali
pa zadati na pr.
ali preko njegovih derivacija. Za žicu
smo imali
pa zadati na pr.
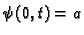 znači zapravo zadati
tj.
Ako je
znači zapravo zadati
tj.
Ako je
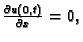 onda kažemo da je lijevi
rub slobodan. Za
takav rubni uvjet kažemo da je homogen.
onda kažemo da je lijevi
rub slobodan. Za
takav rubni uvjet kažemo da je homogen.
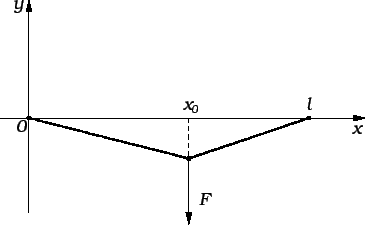
Na sljedećoj slici imamo na desnom rubu homogen Neumannov uvjet.
Neumannov rubni uvjet znači u slučaju
- a)
- oscilacija ili ravnoteže žice, longitudinalnih oscilacija
grede, da je na rubu zadana kontaktna sila,
- b)
- provođenja topline, da se preko ruba prenosi zadana
količina topline; ako je uvjet homogen, onda to znači da je rub
toplinski izoliran,
- c)
- filtracije, da je na rubu zadan protok mase. Ako je rubni
uvjet homogen, onda to znači da tekućina ne protječe kroz rub,
tj. da je rub nepropusan.
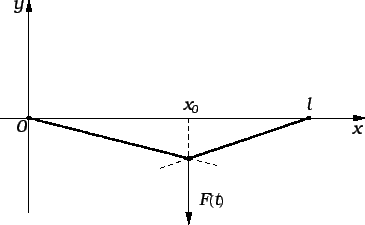
Robinov rubni uvjet.
Ako je na pr. desni rub oprugom spojen s fiksnom podlogom, onda je
količina gibanja u jedinici vremena koja se na desnom kraju prenese
na žicu jednaka sili kojom opruga djeluje na desni kraj
tj.
Na sljedećoj slici imamo na desnom rubu Robinov uvjet.
Primjer 2.4
Lijevi kraj žice se slobodno kreće, a na desnom djeluje sila koja
je proporcionalna brzini, a suprotna smjeru gibanja. Naći rubne
uvjete.
Rješenje. Količina gibanja u jedinici vremena na lijevom kraju je 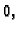 pa
na lijevom kraju imamo rubni uvjet
pa
na lijevom kraju imamo rubni uvjet
Na drugom kraju veličina gibanja u jedinici vremena (sila) koja
pređe s desna na lijevo jednaka je
Prema tome rubni uvjeti su
Početni uvjeti
U svim promatranim slučajevima nije bilo bitno da li se žica nalazi
u ravnotežnom položaju, kad  ne ovisi o varijabli
ne ovisi o varijabli 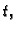 ili se
radi o oscilacijama žice, kad svaki od navedenih rubnih uvjeta mora
vrijediti za svaki
ili se
radi o oscilacijama žice, kad svaki od navedenih rubnih uvjeta mora
vrijediti za svaki 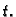 U oba slučaja su trebali biti zadani rubni
uvjeti. Međutim, kad se radi o oscilacijama, onda uvjeti na rubu nisu
dovoljni. Tada moramo također zadati na koji smo način pobudili
žicu na osciliranje. Moramo zadati početni položaj
U oba slučaja su trebali biti zadani rubni
uvjeti. Međutim, kad se radi o oscilacijama, onda uvjeti na rubu nisu
dovoljni. Tada moramo također zadati na koji smo način pobudili
žicu na osciliranje. Moramo zadati početni položaj
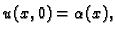 |
(2.5) |
i početnu brzinu
u svakoj točki žice. Ovi uvjeti se zovu početni
uvjeti.
Primijetimo da uvjeti (2.4) i (2.5) nisu
nezavisni. Pretpostavka o neprekidnosti žice prilikom oscilacija
povlači da je
Kad se radi o provođenju topline ili filtraciji, dovoljno je zadati
početnu raspodjelu temperature, odnosno tlaka.
Naravno, početni uvjeti moraju biti kompatibilni s rubnim uvjetima,
tj. početni uvjeti moraju na rubovima zadovoljavati rubne uvjete za
svaki 
Linearnost
Opća jednadžba u primjerima koje smo promatrali, nakon uvrštenja
drugog zakona ponašanja je
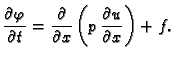 |
(2.6) |
Funkciju 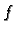 zovemo slobodnim članom. Ako je
zovemo slobodnim članom. Ako je 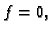 onda
jednadžbu
onda
jednadžbu
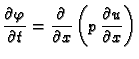 |
(2.7) |
zovemo homogenom, u protivnom je zovemo nehomogenom.
Ograničimo razmatranje na one primjere u kojima je prvi zakon
ponašanja glasio
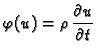 ili ili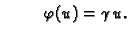 |
(2.8) |
Interesira nas kakvu strukturu ima skup svih rješenja rubnog problema
 |
(2.9) |
U tu svrhu promatrajmo najprije rubni problem s homogenom jednadžbom,
tj. slučaj kad je
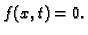
Teorem 14
Neka su
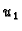
i
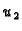
dva rješenja rubnog problema
(
2.9) s pripadnom homogenom jednadžbom, i
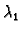
i
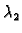
proizvoljni brojevi. Tada je
također rješenje istog rubnog
problema (
2.9).
Dokaz. U svrhu dokaza napišimo
jednadžbu drukčije
Bez obzira
koji 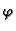 iz (2.8) bio u jednadžbi, vrijedi
Također
Prema tome
Dakle,
iz (2.8) bio u jednadžbi, vrijedi
Također
Prema tome
Dakle,
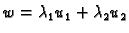 rješava jednadžbu. Ta
funkcija zadovoljava i rubne uvjete, jer je
rješava jednadžbu. Ta
funkcija zadovoljava i rubne uvjete, jer je
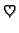
Iz ovog teorema slijedi da je skup svih rješenja homogene jednadžbe
vektorski prostor (skup svih linearnih kombinacija linearno nezavisnih
rješenja).
Za rješenja rubnog problema (2.9) s nehomogenom
jednadžbom imamo sljedeće tvrdnje.
Teorem 15
Neka je
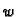
rješenje rubnog problema (
2.9) s
nehomogenom jednadžbom, te

rješenje rubnog problema
(
2.9) s homogenom jednadžbom. Tada je
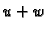
rješenje
rubnog problema (
2.9) s nehomogenom jednadžbom.
Dokaz. Koristeći svojstva funkcije
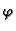 iz dokaza prethodnog teorema, možemo napisati
iz dokaza prethodnog teorema, možemo napisati
Dakle 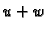 rješava nehomogenu jednadžbu. Osim toga
rješava nehomogenu jednadžbu. Osim toga 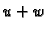 očito zadovoljava i rubne uvjete.
očito zadovoljava i rubne uvjete.
Teorem 16
Neka su
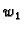
i
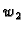
dva rješenja rubnog problema
(
2.9) s nehomogenom jednadžbom. Tada je
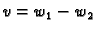
rješenje rubnog problema (
2.9) s homogenom
jednadžbom.
Dokaz.
Osim toga 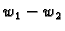 očito zadovoljava i rubne uvjete.
očito zadovoljava i rubne uvjete.
Na temelju ovih teorema imamo sljedeći zaključak.
Neka je 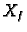 skup svih rješenja rubnog problema (2.9) s
nehomogenom jednadžbom. Neka je
skup svih rješenja rubnog problema (2.9) s
nehomogenom jednadžbom. Neka je 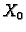 skup svih rješenja rubnog
problema (2.9) s homogenom jednadžbom. Tada je
skup svih rješenja rubnog
problema (2.9) s homogenom jednadžbom. Tada je
gdje je 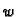 jedno (partikularno)
rješenje rubnog problema (2.9) s nehomogenom jednadžbom.
jedno (partikularno)
rješenje rubnog problema (2.9) s nehomogenom jednadžbom.
Homogenizacija rubnih uvjeta.
Ako su rubni uvjeti
nehomogeni, onda linearne kombinacije više ne zadovoljavaju iste
rubne uvjete, pa gornji teoremi više ne vrijede. Prema tome pogodno
je imati homogene rubne uvjete. To se može postići na sljedeći
način. Neka je dan na pr. sljedeći rubni problem
Izaberimo proizvoljnu što jednostavniju funkciju 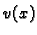 klase
klase 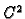 ali tako da zadovoljava rubne uvjete
Stavimo
ali tako da zadovoljava rubne uvjete
Stavimo
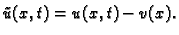 Tada funkcija
Tada funkcija 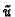 zadovoljava
homogene rubne uvjete
S druge strane,
da bismo vidjeli koju jednadžbu zadovoljava
zadovoljava
homogene rubne uvjete
S druge strane,
da bismo vidjeli koju jednadžbu zadovoljava
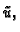 uvrstimo
uvrstimo
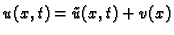 u jednadžbu iz rubnog
problema
gdje je
u jednadžbu iz rubnog
problema
gdje je
Primjer 2.5
Homogenizirati rubni problem
Rješenje. Izaberimo najjednostavniju funkciju 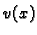 takvu da funkcija
takvu da funkcija
zadovoljava homogene rubne uvjete, tj.
Zbog toga što se radi o uvjetu u samo dvije točke, dovoljno je uzeti
Tako je
Odatle
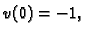
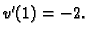
Slijedi
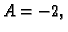
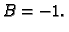
Tako je
pa kad
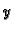
izračunamo odavde i uvrstimo u jednadžbu, imamo rubni problem
Jedinstvenost rješenja
Ograničimo se sada na problem ravnoteže u sredstvu s otporom i
razmotrimo jedinstvenost rješenja sljedećih rubnih
problema. Diferencijalna jednadžba je uvijek
a rubni uvjeti
su redom
- I
-

- II
-

- III
-

Slučaj
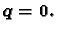 (nema otpora sredstva)
(nema otpora sredstva)
Jednadžba je tada
pa imamo
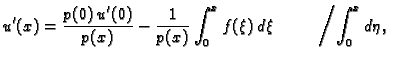 |
(2.10) |
tj.
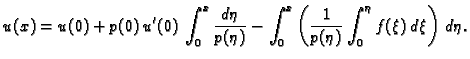 |
(2.11) |
U ovoj formuli imamo dvije neodređene veličine 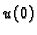 i
i
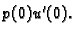 Razmotrimo sada jedinstvenost uz navedene rubne uvjete.
Razmotrimo sada jedinstvenost uz navedene rubne uvjete.
I. (Oba uvjeta kinematička.)
Imamo
Veličina 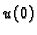 je
određena u rubnom uvjetu, a
je
određena u rubnom uvjetu, a 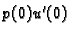 se određuje tako da uvrstimo
se određuje tako da uvrstimo
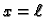 u formulu (2.11). Dobivamo
Odatle
Budući da su neodređene
veličine u formuli (2.11) pomoću rubnih uvjeta u
potpunosti određene, zaključujemo da je rješenje u tom slučaju
jedinstveno.
u formulu (2.11). Dobivamo
Odatle
Budući da su neodređene
veličine u formuli (2.11) pomoću rubnih uvjeta u
potpunosti određene, zaključujemo da je rješenje u tom slučaju
jedinstveno.
II. Jedan uvjet kinematički, drugi dinamički.
Imamo
Ovdje je također 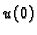 određen, a
određen, a 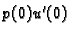 ćemo dobiti tako da u formulu
(2.10) uvrstimo
ćemo dobiti tako da u formulu
(2.10) uvrstimo 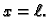 Odatle
Opet zaključujemo da je rješenje
jedinstveno, jer smo neodređene veličine u formuli
(2.11) jednoznačno odredili.
Odatle
Opet zaključujemo da je rješenje
jedinstveno, jer smo neodređene veličine u formuli
(2.11) jednoznačno odredili.
III. Oba uvjeta dinamička.
Imamo
Sada možemo
koristiti samo formulu (2.10). Iz nje ne možemo odrediti
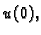 dok za određivanje
dok za određivanje 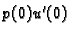 imamo čak dva podatka. To
pokazuje da više nemamo jedinstvenost, jer
imamo čak dva podatka. To
pokazuje da više nemamo jedinstvenost, jer 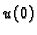 ostaje neodređeno. S druge strane može se dogoditi da
ostaje neodređeno. S druge strane može se dogoditi da
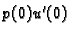 izračunat pomoću uvjeta na desnom rubu ne bude isti kao
onaj izračunat pomoću uvjeta na lijevom rubu. To bi, naravno
značilo da ne postoji rješenje. Kad uvrstimo uvjet na lijevom rubu,
imamo
Kad uvrstimo uvjet na desnom
rubu, imamo
Dakle, za postojanje rješenja
nužno je da vrijedi
Taj zahtjev znači da zbroj
vanjskih sila mora biti jednak
izračunat pomoću uvjeta na desnom rubu ne bude isti kao
onaj izračunat pomoću uvjeta na lijevom rubu. To bi, naravno
značilo da ne postoji rješenje. Kad uvrstimo uvjet na lijevom rubu,
imamo
Kad uvrstimo uvjet na desnom
rubu, imamo
Dakle, za postojanje rješenja
nužno je da vrijedi
Taj zahtjev znači da zbroj
vanjskih sila mora biti jednak 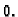 Prva dva člana predstavljaju
kontaktnu silu koja preko rubova djeluje na žicu, a integral
predstavlja vanjsku silu koja djeluje na daljinu (sila
gravitacije, sila električnog polja i sl.).
Prva dva člana predstavljaju
kontaktnu silu koja preko rubova djeluje na žicu, a integral
predstavlja vanjsku silu koja djeluje na daljinu (sila
gravitacije, sila električnog polja i sl.).
Ako je taj uvjet ispunjen onda kažemo da je rješenje jedinstveno do
na aditivnu konstantu (u ovom slučaju 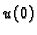 ).
).
Uvjet 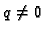 znači ustvari da je
znači ustvari da je 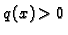 za barem jedan
za barem jedan 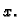 U
ovom slučaju sva tri rubna problema imaju jedinstveno rješenje. To
ćemo dokazati pomoću energetske
jednadžbe.
U
ovom slučaju sva tri rubna problema imaju jedinstveno rješenje. To
ćemo dokazati pomoću energetske
jednadžbe.
Jednom parcijalno integriramo prvi integral
i rezultat uvrstimo. Dobivamo
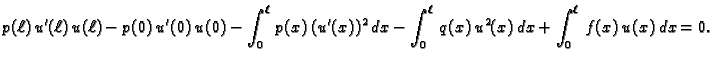 |
(2.12) |
Ova jednadžba se zove energetska jednadžba. Naziv ima opravdanje u sljedećem razmatranju.
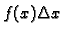 predstavlja
približno vanjsku silu koja djeluje na komadić žice
predstavlja
približno vanjsku silu koja djeluje na komadić žice 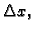 a
a
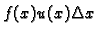 je rad te sile na putu progiba
je rad te sile na putu progiba 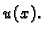 Prema tome
zadnji integral na lijevoj strani jednadžbe (2.12) je rad
vanjske sile koji djeluje na cijelu žicu na putu progiba. Sila otpora
je
Prema tome
zadnji integral na lijevoj strani jednadžbe (2.12) je rad
vanjske sile koji djeluje na cijelu žicu na putu progiba. Sila otpora
je
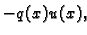 pa je srednji integral ukupni rad sile otpora duž
cijele žice na putu progiba. Prvi integral predstavlja energiju
deformacije,
pa je srednji integral ukupni rad sile otpora duž
cijele žice na putu progiba. Prvi integral predstavlja energiju
deformacije,
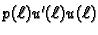 je rad kontaktne sile
na desnom rubu na putu
je rad kontaktne sile
na desnom rubu na putu
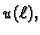 a
a
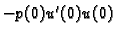 je rad
kontaktne sile na lijevom rubu na putu
je rad
kontaktne sile na lijevom rubu na putu 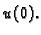
Neka su 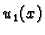 i
i 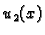 dva rješenja bilo kojeg od tri rubna
problema koja promatramo. Funkcija
dva rješenja bilo kojeg od tri rubna
problema koja promatramo. Funkcija
rješava
homogenu jednadžbu
i
pri tom zadovoljava homogene rubne uvjete. Energetska jednadžba
(2.12) sada glasi
Budući da je 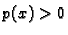 i
i
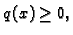 slijedi
Kako je podintegralna funkcija neprekidna,
nenegativna, i njezin je integral duž žice jednak
slijedi
Kako je podintegralna funkcija neprekidna,
nenegativna, i njezin je integral duž žice jednak 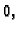 slijedi da je
sama podintegralna funkcija jednaka nuli
Zbroj dvije
nenegativne funkcije može biti jednak nuli samo tako da je svaka od
njih jednaka nuli. Tako je
pa je
slijedi da je
sama podintegralna funkcija jednaka nuli
Zbroj dvije
nenegativne funkcije može biti jednak nuli samo tako da je svaka od
njih jednaka nuli. Tako je
pa je 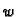 konstanta, tj.
konstanta, tj. 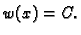 S druge strane je
Kako je
S druge strane je
Kako je 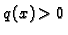 za barem jedan
za barem jedan  slijedi da je
slijedi da je 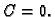 Prema tome
tj.
Dakle rješenje je doista jedinstveno.
Prema tome
tj.
Dakle rješenje je doista jedinstveno.
Koncentrirano djelovanje
U dosadašnjim razmatranjima vanjska sila je bila zadana po jedinici
duljine, što znači da je 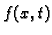 gustoća sile (linearna kad se
radi o jednodimenzionalnom objektu kao što je žica). Ako je u točki
gustoća sile (linearna kad se
radi o jednodimenzionalnom objektu kao što je žica). Ako je u točki
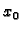 napete žice obješen uteg mase
napete žice obješen uteg mase 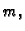 onda kažemo da se radi o
koncentriranom djelovanju. U tom slučaju ne vrijedi izvod
zakona o sačuvanju količine gibanja u 2.1.1.
onda kažemo da se radi o
koncentriranom djelovanju. U tom slučaju ne vrijedi izvod
zakona o sačuvanju količine gibanja u 2.1.1.
Pretpostavimo da masa utega nije prevelika, tako da se ne događa
kidanje žice niti plastična deformacija. To znači da je progib
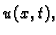 kao funkcija od
kao funkcija od  neprekidna
funkcija, tj.
neprekidna
funkcija, tj.
Ovu jednakost zapisujemo ovako
Promatrajmo mali komad žice
![$ [x_0-\varepsilon,x_0+\varepsilon]$](img1361.gif) oko
točke
oko
točke 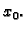 Promjena količine gibanja tog komada žice u jedinici
vremena jednaka je sili koja djeluje na taj komad
Promjena količine gibanja tog komada žice u jedinici
vremena jednaka je sili koja djeluje na taj komad
tj.
gdje smo s
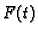 označili koncentriranu silu u točki
označili koncentriranu silu u točki 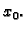
Promjena količine
gibanja u jedinici vremena je veličina koja se neprekidno mijenja u
vremenu, pa je
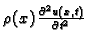 neprekidna funkcija. Odatle, po teoremu srednje
vrijednosti za integrale
neprekidna funkcija. Odatle, po teoremu srednje
vrijednosti za integrale
Dakle imamo
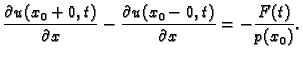 |
(2.13) |
Ova jednakost
pokazuje da derivacija polja  po
po 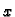 ima u točki
ima u točki 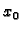 prekid.
Geometrijski to znači da je progib krivulja, koja u točki
prekid.
Geometrijski to znači da je progib krivulja, koja u točki 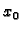 nema
tangentu. Izvan točke
nema
tangentu. Izvan točke 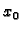 progib ima tangentu, i kad prolazimo kroz
točku
progib ima tangentu, i kad prolazimo kroz
točku 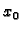 koeficijent smjera tangente skoči.
Izvan točke
koeficijent smjera tangente skoči.
Izvan točke 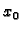 vrijedi izvedena diferencijalna jednadžba za
žicu, ali s vanjskom silom
vrijedi izvedena diferencijalna jednadžba za
žicu, ali s vanjskom silom 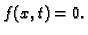
Za funkciju, koja u točki 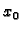 ima konačan limes slijeve strane i
konačan limes s desne strane,ali se ti limesi razlikuju, kažemo da
ima u točki
ima konačan limes slijeve strane i
konačan limes s desne strane,ali se ti limesi razlikuju, kažemo da
ima u točki 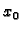 prekid prve vrste.
prekid prve vrste.
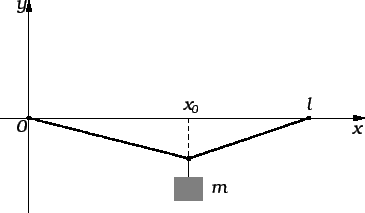
Primjer 2.6
Naći ravnotežu napete žice, duljine
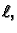
napetosti
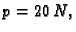
učvršćene na rubovima,
ako okomito na žicu djeluju koncentrirane sile i to
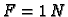
u točki
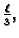
a
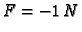
u točki
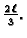
Rješenje. Na intervalima
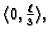
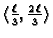 i
i
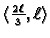 nemamo koncentriranih niti drugih
vanjskih sila, pa je na njima jednadžba
nemamo koncentriranih niti drugih
vanjskih sila, pa je na njima jednadžba
Dakle imamo rješenje
Neodređene konstante
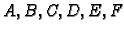
se računaju iz rubnih uvjeta, uvjeta
neprekidnosti i (
2.13). Tako imamo sljedeće jednadžbe
Rješenje ovog sustava je
Dakle imamo rješenje
Greenova funkcija
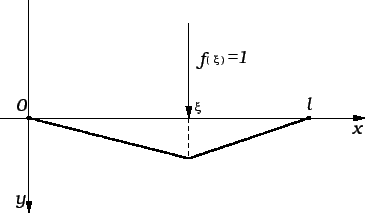
Promatrajmo ravnotežu žice, učvršćene na rubovima, pod utjecajem
koncentrirane sile 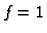 u točki
u točki 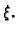 Označimo njezin progib s
Označimo njezin progib s
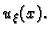
Budući da zakon održanja ne vrijedi na cijeloj žici, već samo na
dijelovima
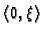 i
i
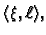 progib
progib
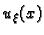 ćemo dobiti kao rješenje sljedećih rubnih problema
ćemo dobiti kao rješenje sljedećih rubnih problema
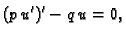
za
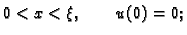
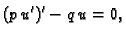
za
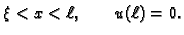
Svaki od ovih rubnih problema ima beskonačno
mnogo rješenja (jer nije dan uvjet na rubu 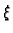 ). Iz zahtjeva da je
). Iz zahtjeva da je
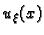 neprekidna, i da njezina derivacija ima skok prve vrste u točki
neprekidna, i da njezina derivacija ima skok prve vrste u točki 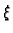 dobivamo jedno rješenje
dobivamo jedno rješenje
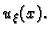
Pustimo da jedinična sila klizi duž žice, tj. da 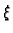 varira od
0 do
varira od
0 do 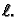 Dobivamo funkciju od dvije varijable
Dobivamo funkciju od dvije varijable
Funkcija 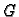 je definirana na
je definirana na
![$ [0,\ell{}]\times{}[0,\ell{}],$](img1414.gif) i zove se Greenova funkcija.
i zove se Greenova funkcija.
Primjer 2.7
Izračunajmo Greenovu funkciju za rubni problem
Rješenje. Lijevo od točke 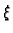 je
je
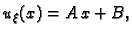 a desno
a desno
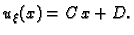 Nakon uvrštenja rubnih uvjeta, imamo
Nakon uvrštenja rubnih uvjeta, imamo
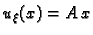 lijevo od
lijevo od 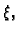 i
i
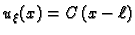 desno od
desno od 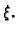 Dakle Greenova funkcija je
Dakle Greenova funkcija je
Neodređene veličine
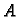
i
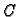
određujemo iz uvjeta neprekidnosti u točki
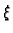
i skoka prve derivacije
Odatle
pa je
Neka su 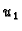 i
i 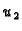 dva linearno nezavisna rješenja homogene jednadžbe
dva linearno nezavisna rješenja homogene jednadžbe
takva da 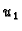 zadovoljava homogeni rubni
uvjet na lijevom rubu, a
zadovoljava homogeni rubni
uvjet na lijevom rubu, a 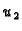 homogeni rubni uvjet na desnom rubu.
Zbog homogenosti jednadžbe i rubnih uvjeta funkcije
homogeni rubni uvjet na desnom rubu.
Zbog homogenosti jednadžbe i rubnih uvjeta funkcije 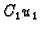 i
i 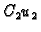 zadovoljavaju jednadžbu i odgovarajući rubni uvjet ma kakvi bili brojevi
zadovoljavaju jednadžbu i odgovarajući rubni uvjet ma kakvi bili brojevi 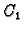 i
i 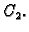 Zato Greenovu funkciju tražimo u obliku
Uvjet neprekidnosti rješenja i skoka njegove prve derivacije daje
sustav od dvije linearne algebarske jednadžbe za nepoznanice
Zato Greenovu funkciju tražimo u obliku
Uvjet neprekidnosti rješenja i skoka njegove prve derivacije daje
sustav od dvije linearne algebarske jednadžbe za nepoznanice 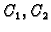
Ovaj sustav je nehomogen, pa ima rješenje ako i samo ako je
determinanta sustava različita od nule. Determinanta sustava je
gdje je 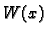 determinanta Wronskoga
Ona je uvijek
različita od nule (zbog
linearne nezavisnosti
determinanta Wronskoga
Ona je uvijek
različita od nule (zbog
linearne nezavisnosti 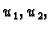 v. Matematika 2). Prema tome postoji rješenje i ono se može naći na pr. pomoću
Cramerovog pravila
Tako je
v. Matematika 2). Prema tome postoji rješenje i ono se može naći na pr. pomoću
Cramerovog pravila
Tako je
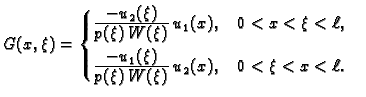 |
(2.14) |
Primjer 2.8
Naći Greenovu funkciju rubnog problema
Rješenje. Rješenje diferencijalne jednadžbe je
Linearno nezavisne funkcije, koje zadovoljavaju rubne uvjete su prema
tome
Iz uvjeta neprekidnosti i skoka prve derivacije u točki
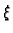
dobivamo sustav jednadžbi
Rješenje tog sustava je
i prema tome Greenova funkcija je
Ako u točki 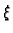 na žicu djeluje koncentrirana sila
na žicu djeluje koncentrirana sila 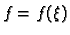 umjesto jedinične sile, onda je rješenje (progib)
umjesto jedinične sile, onda je rješenje (progib)
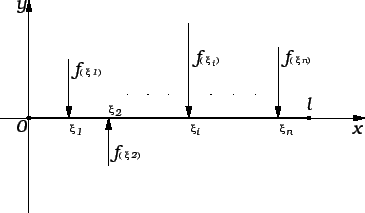
Ako na žicu djeluje više koncentriranih sila
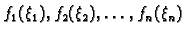 u točkama
u točkama
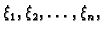 onda je rješenje
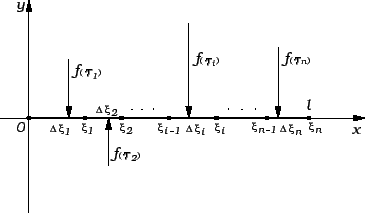
Konačno, ako vanjska sila nije koncentrirana, već je zadana kao
linearna gustoća sile, tj. ako imamo na pr. rubni problem
onda podijelimo segment
onda je rješenje
Konačno, ako vanjska sila nije koncentrirana, već je zadana kao
linearna gustoća sile, tj. ako imamo na pr. rubni problem
onda podijelimo segment
![$ [0,\ell{}]$](img1456.gif) na
na 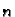 podsegmenata,
uzmemo proizvoljne točke
podsegmenata,
uzmemo proizvoljne točke 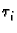 u tim segmentima, i
umjesto zadane sile uzmemo koncentriranu silu
u tim segmentima, i
umjesto zadane sile uzmemo koncentriranu silu
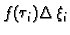 u
točki
u
točki 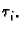 Približno rješenje je
Na
desnoj strani imamo integralnu sumu za funkciju
Približno rješenje je
Na
desnoj strani imamo integralnu sumu za funkciju
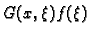 u
odnosu na varijablu
u
odnosu na varijablu 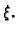 Kad podjelu sve više profinjujemo,
integralna suma teži prema integralu, pa je rješenje
Kad podjelu sve više profinjujemo,
integralna suma teži prema integralu, pa je rješenje
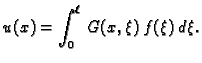 |
(2.15) |
Iz formule (2.15) se vidi da su u Greenovoj funkciji
sadržane informacije o pripadnoj homogenoj diferencijalnoj jednadžbi
i o danim rubnim uvjetima.
Kako Greenova funkcija ima različite formule ovisno o tome da li se 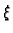 nalazi ispred
nalazi ispred 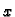 ili iza, integral treba rastaviti na dva dijela, od 0 do
ili iza, integral treba rastaviti na dva dijela, od 0 do 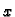 i od
i od 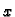 do
do 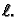
Integrira se po 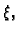 pa
pa 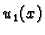 i
i 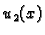 smijemo izlučiti. Tako
imamo konačnu formulu
smijemo izlučiti. Tako
imamo konačnu formulu
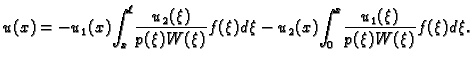 |
(2.16) |
Dakle, kad želimo riješiti neki rubni problem pomoću Greenove
funkcije, dovoljno je naći dva
linearno nezavisna rješenja 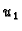 i
i 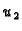 pripadne homogene
jednadžbe, takva da
pripadne homogene
jednadžbe, takva da 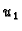 zadovoljava homogeni uvjet na lijevom rubu, a
zadovoljava homogeni uvjet na lijevom rubu, a
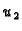 na desnom rubu. Zatim treba izračunati
determinantu
na desnom rubu. Zatim treba izračunati
determinantu 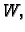 i uvrstiti u formulu (2.16).
i uvrstiti u formulu (2.16).
Primjer 2.9
Riješiti, pomoću Greenove formule, rubni problem
Rješenje. Najprije treba primijetiti da je
Opće rješenje pripadne homogene jednadžbe je
Najjednostavnija ovakva funkcija, koja zadovoljava uvjet
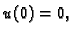
je
ona koja zadovoljava uvjet
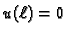
je
Nadalje imamo
Uvrstimo u (
2.16)
Ova funkcija očito zadovoljava rubne uvjete, a nakon uvrštavanja,
lako provjerimo da zadovoljava i jednadžbu.
Primijetimo također da za nalaženje funkcija 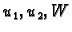 uopće nije
bilo važno koliki je
uopće nije
bilo važno koliki je 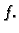 Funkcija
Funkcija 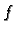 se uvrsti tek na kraju u
formulu. Prema tome, kad jednom nađemo
se uvrsti tek na kraju u
formulu. Prema tome, kad jednom nađemo
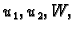 umetanjem u
formulu raznih funkcija
umetanjem u
formulu raznih funkcija 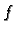 rješavamo svaki mogući nehomogeni problem.
rješavamo svaki mogući nehomogeni problem.




Next: Fourierova metoda
Up: Rubni problemi
Previous: Jednadžbe
Contents
Index
Salih Suljagic
1999-12-17
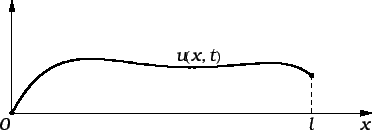
![]() na rubovima, na
pr.
na rubovima, na
pr.
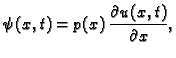
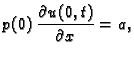
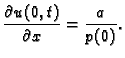

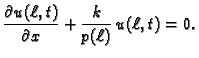

![]() pa
na lijevom kraju imamo rubni uvjet
pa
na lijevom kraju imamo rubni uvjet
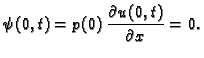
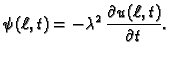
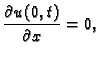
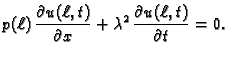
![]() ne ovisi o varijabli
ne ovisi o varijabli ![]() ili se
radi o oscilacijama žice, kad svaki od navedenih rubnih uvjeta mora
vrijediti za svaki
ili se
radi o oscilacijama žice, kad svaki od navedenih rubnih uvjeta mora
vrijediti za svaki ![]() U oba slučaja su trebali biti zadani rubni
uvjeti. Međutim, kad se radi o oscilacijama, onda uvjeti na rubu nisu
dovoljni. Tada moramo također zadati na koji smo način pobudili
žicu na osciliranje. Moramo zadati početni položaj
U oba slučaja su trebali biti zadani rubni
uvjeti. Međutim, kad se radi o oscilacijama, onda uvjeti na rubu nisu
dovoljni. Tada moramo također zadati na koji smo način pobudili
žicu na osciliranje. Moramo zadati početni položaj
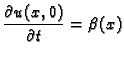
![]()
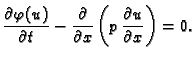
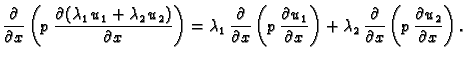
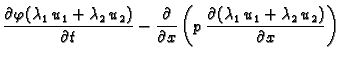
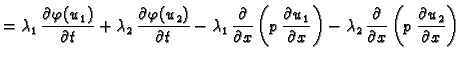
![$\displaystyle = \lambda_1\,\left[\frac{\partial\varphi
(u_1)}{\partial t} - \fr...
...partial}{\partial x}\left(p\,\frac{\partial u_2}{\partial
x}\right)\right] = 0.$](img1259.gif)
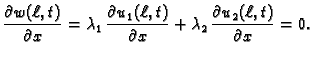
![]() iz dokaza prethodnog teorema, možemo napisati
iz dokaza prethodnog teorema, možemo napisati
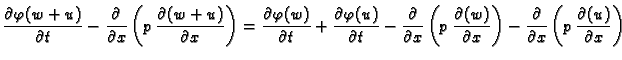
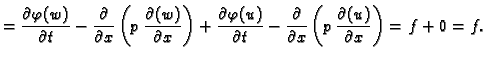
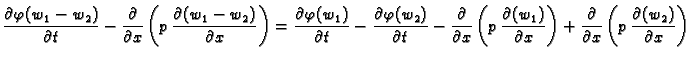
![$\displaystyle = \frac{\partial\varphi(w_1)}{\partial t} -
\frac{\partial}{\part...
...partial x}\left(p\,\frac{\partial (w_2)}{\partial
x}\right)\right] = f - f = 0.$](img1271.gif)
![]() skup svih rješenja rubnog problema (2.9) s
nehomogenom jednadžbom. Neka je
skup svih rješenja rubnog problema (2.9) s
nehomogenom jednadžbom. Neka je ![]() skup svih rješenja rubnog
problema (2.9) s homogenom jednadžbom. Tada je
skup svih rješenja rubnog
problema (2.9) s homogenom jednadžbom. Tada je
![% latex2html id marker 34022
$\displaystyle \begin{array}{l}
\rho\,\frac{\textst...
...ial x}}\right)+f(x,t),\\ [3mm]
u(0,t)=a,\hspace{1cm}u(\ell,t)=b.
\end{array}$](img1274.gif)
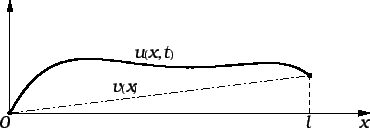
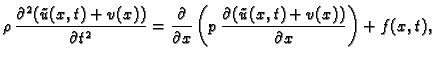
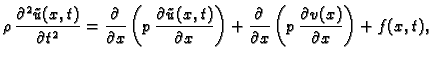
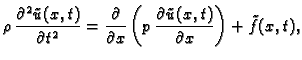
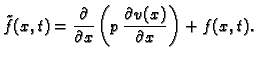
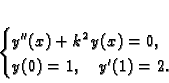
![]() takvu da funkcija
takvu da funkcija
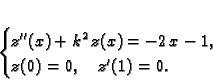
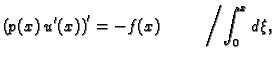
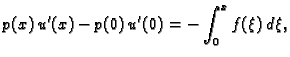
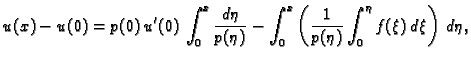
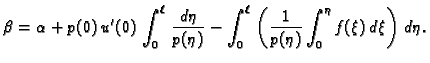
![$\displaystyle p(0)\,u'(0) = \frac{1}{\int_0^{\ell}\,\frac{d\eta}{p(\eta)}}
\,\l...
...ll}\,\left(\frac{1}{p({\eta})}\int_0^{\eta}
f(\xi)\,d\xi\right) \,d\eta\right].$](img1316.gif)
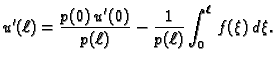
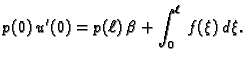
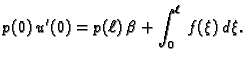
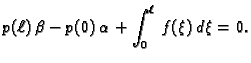
![]() ).
).
![]() znači ustvari da je
znači ustvari da je ![]() za barem jedan
za barem jedan ![]() U
ovom slučaju sva tri rubna problema imaju jedinstveno rješenje. To
ćemo dokazati pomoću energetske
jednadžbe.
U
ovom slučaju sva tri rubna problema imaju jedinstveno rješenje. To
ćemo dokazati pomoću energetske
jednadžbe.
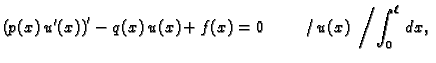
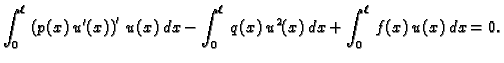
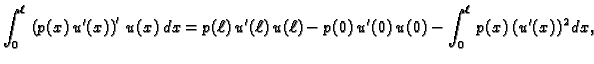
![]() i
i ![]() dva rješenja bilo kojeg od tri rubna
problema koja promatramo. Funkcija
dva rješenja bilo kojeg od tri rubna
problema koja promatramo. Funkcija
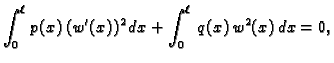
![$\displaystyle \int_0^{\ell}\,\left[p(x)\,(w'(x))^2 +
q(x)\,w^2(x)\right]\, dx = 0.$](img1346.gif)
![]() gustoća sile (linearna kad se
radi o jednodimenzionalnom objektu kao što je žica). Ako je u točki
gustoća sile (linearna kad se
radi o jednodimenzionalnom objektu kao što je žica). Ako je u točki
![]() napete žice obješen uteg mase
napete žice obješen uteg mase ![]() onda kažemo da se radi o
koncentriranom djelovanju. U tom slučaju ne vrijedi izvod
zakona o sačuvanju količine gibanja u 2.1.1.
onda kažemo da se radi o
koncentriranom djelovanju. U tom slučaju ne vrijedi izvod
zakona o sačuvanju količine gibanja u 2.1.1.
![]() kao funkcija od
kao funkcija od ![]() neprekidna
funkcija, tj.
neprekidna
funkcija, tj.
![]() oko
točke
oko
točke ![]() Promjena količine gibanja tog komada žice u jedinici
vremena jednaka je sili koja djeluje na taj komad
Promjena količine gibanja tog komada žice u jedinici
vremena jednaka je sili koja djeluje na taj komad
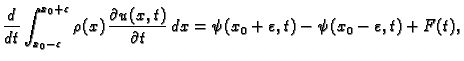
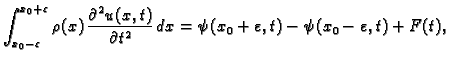
![]() neprekidna funkcija. Odatle, po teoremu srednje
vrijednosti za integrale
neprekidna funkcija. Odatle, po teoremu srednje
vrijednosti za integrale
![$\displaystyle \lim_{\varepsilon\rightarrow 0+}
\int_{x_0-\varepsilon}^{x_0+\var...
...\,\varepsilon\,\rho(\xi)\,\frac{\partial^2 u(\xi,t)}{\partial
t^2}\right] = 0.$](img1368.gif)
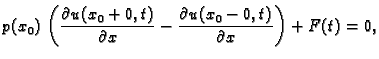
![]() ima konačan limes slijeve strane i
konačan limes s desne strane,ali se ti limesi razlikuju, kažemo da
ima u točki
ima konačan limes slijeve strane i
konačan limes s desne strane,ali se ti limesi razlikuju, kažemo da
ima u točki ![]() prekid prve vrste.
prekid prve vrste.
![]()
![]() i
i
![]() nemamo koncentriranih niti drugih
vanjskih sila, pa je na njima jednadžba
nemamo koncentriranih niti drugih
vanjskih sila, pa je na njima jednadžba
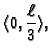
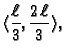
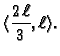
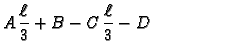
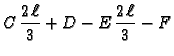
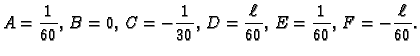
![% latex2html id marker 34358
$\displaystyle u(x) = \begin{cases}\frac{1}{60}\,x,...
... -\frac{\ell}{60},& \quad \text{za } x\in [\frac{2\,\ell}{3},\ell]. \end{cases}$](img1398.gif)
![]() u točki
u točki ![]() Označimo njezin progib s
Označimo njezin progib s
![]()
![]() varira od
0 do
varira od
0 do ![]() Dobivamo funkciju od dvije varijable
Dobivamo funkciju od dvije varijable
![]() je
je
![]() a desno
a desno
![]() Nakon uvrštenja rubnih uvjeta, imamo
Nakon uvrštenja rubnih uvjeta, imamo
![]() lijevo od
lijevo od ![]() i
i
![]() desno od
desno od ![]() Dakle Greenova funkcija je
Dakle Greenova funkcija je
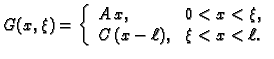
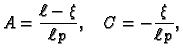
![% latex2html id marker 34433
$\displaystyle G(x,\xi) = \left\{
\begin{array}{ll}...
...ll, \\ [2mm]
\frac{\xi}{\ell\,p}\,(\ell-x), & 0<\xi<x<\ell.
\end{array}\right.$](img1425.gif)
![]() i
i ![]() dva linearno nezavisna rješenja homogene jednadžbe
dva linearno nezavisna rješenja homogene jednadžbe
![% latex2html id marker 34454
$\displaystyle G(x,\xi) = \left\{
\begin{array}{ll}
C_1\,u_1(x), & 0<x<\xi, \\ [2mm]
C_2\,u_2(x), & \xi<x<\ell.
\end{array}\right.$](img1429.gif)
![% latex2html id marker 34471
$\displaystyle \left\vert
\begin{array}{ll}
u_1(\xi...
...i) & u_2(\xi) \\ [1mm]
u'_1(\xi) & u'_2(\xi)
\end{array}\right\vert = -W(\xi),$](img1435.gif)
![% latex2html id marker 34475
$\displaystyle W(x) = \left\vert
\begin{array}{ll}
u_1(x) & u_2(x) \\ [1mm]
u'_1(x) & u'_2(x)
\end{array}\right\vert.$](img1437.gif)
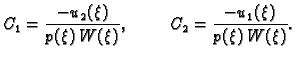
![\begin{displaymath}
% latex2html id marker 34484\begin{cases}
\displaystyle \l...
... [2mm]
u'(0) = 0,\qquad u(\ell) + k\,u'(\ell) = 0.
\end{cases}\end{displaymath}](img1441.gif)
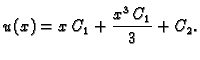
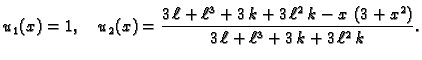
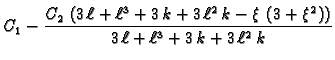
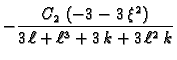
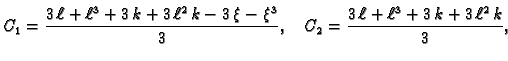
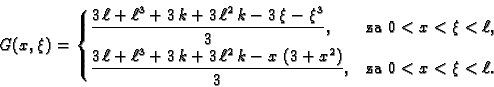
![]() na žicu djeluje koncentrirana sila
na žicu djeluje koncentrirana sila ![]() umjesto jedinične sile, onda je rješenje (progib)
umjesto jedinične sile, onda je rješenje (progib)
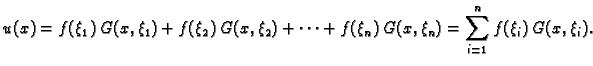
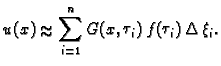
![]() nalazi ispred
nalazi ispred ![]() ili iza, integral treba rastaviti na dva dijela, od 0 do
ili iza, integral treba rastaviti na dva dijela, od 0 do ![]() i od
i od ![]() do
do ![]()
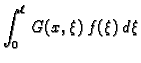
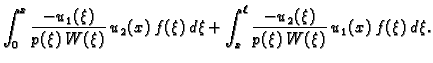
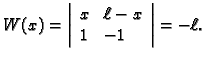
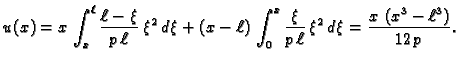
![]() uopće nije
bilo važno koliki je
uopće nije
bilo važno koliki je ![]() Funkcija
Funkcija ![]() se uvrsti tek na kraju u
formulu. Prema tome, kad jednom nađemo
se uvrsti tek na kraju u
formulu. Prema tome, kad jednom nađemo
![]() umetanjem u
formulu raznih funkcija
umetanjem u
formulu raznih funkcija ![]() rješavamo svaki mogući nehomogeni problem.
rješavamo svaki mogući nehomogeni problem.