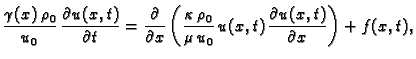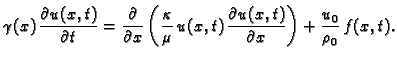



Next: Rubni problemi
Up: Rubni problemi
Previous: Rubni problemi
Contents
Index
Subsections
Jednadžbe
Poprečne oscilacije žice
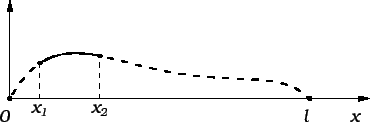
Promatrat ćemo gibanje napete žice duljine 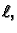 koje nastaje
uslijed nekog vanjskog djelovanja. Pretpostavit ćemo da vanjsko djelovanje
nije tako veliko da dolazi do plastičnih deformacija ili do kidanja
žice. Ako se progib ne mijenja s vremenom, onda govorimo o
ravnoteži žice. U protivnom govorimo o
oscilacijama žice.
koje nastaje
uslijed nekog vanjskog djelovanja. Pretpostavit ćemo da vanjsko djelovanje
nije tako veliko da dolazi do plastičnih deformacija ili do kidanja
žice. Ako se progib ne mijenja s vremenom, onda govorimo o
ravnoteži žice. U protivnom govorimo o
oscilacijama žice.
U vezi s gibanjem žice imamo sljedeća vektorska
polja od dvije varijable, definirana na
![$ [0,\ell]\times R$](img1037.gif) s
vrijednostima u
s
vrijednostima u 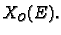 Prva varijabla je varijabla položaja
Prva varijabla je varijabla položaja
![$ x\in
[0,\ell]\,$](img1039.gif) a druga varijabla vremena
a druga varijabla vremena 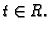
-
-
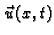 - progib žice u točki
- progib žice u točki  u čas
u čas 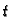 (polje pomaka),
(polje pomaka),
-
-
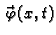 - ukupna
količina gibanja po jedinici duljine, u točki
- ukupna
količina gibanja po jedinici duljine, u točki  u čas
u čas 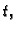 (gustoća (linearna) količine gibanja)
(gustoća (linearna) količine gibanja)
-
-
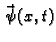 - količina gibanja, koja se u točki
- količina gibanja, koja se u točki  prenese s desna na lijevo u jedinici vremena u čas
prenese s desna na lijevo u jedinici vremena u čas 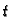 (kontaktna
sila),
(kontaktna
sila),
-
-
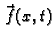 - količina gibanja po jedinici duljine, koja se u
jedinici vremena izvana prenese na žicu u točki
- količina gibanja po jedinici duljine, koja se u
jedinici vremena izvana prenese na žicu u točki  u
čas
u
čas 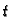 (gustoća (linearna) vanjske sile).
(gustoća (linearna) vanjske sile).
Prvo vektorsko polje 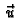 se zove kinematičko
polje, i ono opisuje progib žice. Ostala tri polja
se zove kinematičko
polje, i ono opisuje progib žice. Ostala tri polja
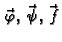 se zovu dinamička
polja. Pri tom drugo vektorsko polje opisuje ukupnu količinu
gibanja. Treće vektorsko
polje opisuje količinu gibanja koja nastaje tako što se uslijed
neprekidnosti žice i njezine napetosti količina gibanja desnog
dijela žice preko točke
se zovu dinamička
polja. Pri tom drugo vektorsko polje opisuje ukupnu količinu
gibanja. Treće vektorsko
polje opisuje količinu gibanja koja nastaje tako što se uslijed
neprekidnosti žice i njezine napetosti količina gibanja desnog
dijela žice preko točke 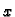 prenosi na lijevi dio. Četvrto vektorsko
polje opisuje količinu gibanja koja nastaje uslijed djelovanja
vanjske sile (gravitacija i sl.).
prenosi na lijevi dio. Četvrto vektorsko
polje opisuje količinu gibanja koja nastaje uslijed djelovanja
vanjske sile (gravitacija i sl.).
Zakon održanja količine gibanja
Uočimo proizvoljan komad žice
![$ D=[x_1,x_2].$](img1049.gif)
Ukupna količina gibanja
tog dijela žice u čas 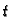 je
a ukupna količina gibanja komada žice
je
a ukupna količina gibanja komada žice 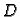 po jedinici vremena
je derivacija ukupne količine gibanja po vremenu
po jedinici vremena
je derivacija ukupne količine gibanja po vremenu
Količina gibanja po jedinici vremena komada žice 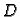 u čas
u čas 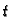 uslijed djelovanja vanjske sile je
uslijed djelovanja vanjske sile je
Količina gibanja koja se po jedinici vremena prenese na 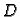 u čas
u čas
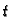 na desnom rubu, u točki
na desnom rubu, u točki 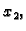 je
je
a količina gibanja koja se po jedinici
vremena prenese na 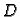 u čas
u čas 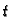 na lijevom rubu, u točki
na lijevom rubu, u točki 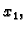 je
jer smo za pozitivan smjer prenošenja
količine gibanja duž žice izabrali smjer s desna na lijevo.
je
jer smo za pozitivan smjer prenošenja
količine gibanja duž žice izabrali smjer s desna na lijevo.
Slika 2.2:
Kontaktna sila na rubovima
Ukupna količina gibanja po jedinici vremena komada 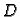 jednaka je zbroju
količina gibanja po jedinici vremena uslijed djelovanja preostalog
dijela žice i uslijed djelovanja vanjske sile. Dakle
jednaka je zbroju
količina gibanja po jedinici vremena uslijed djelovanja preostalog
dijela žice i uslijed djelovanja vanjske sile. Dakle
Ova
jednadžba se zove jednadžba balansa ili zakon održanja količine gibanja. (Uočite da se ovdje
radi o poznatom fizikalnom zakonu da je promjena količine gibanja
nekog tijela u jedinici vremena jednaka zbroju sila koje djeluju na tijelo.)
Pretostavka da je ukupna količina gibanja po jedinici vremena
neprekidna
funkcija, što fizikalno znači da se brzina promjene količine
gibanja neprekidno mijenja (neprekidnost sile), omogućava da
primijenimo Leibnizovo
pravilo za deriviranje pod znakom integrala. Zatim, ako još
shvatimo kao jednu stranu Newton-Leibnizove formule (osnovne formule
integralnog računa), onda imamo
odnosno
Naglasimo da ovaj izvod vrijedi za proizvoljan segment žice
![$ [x_1,x_2].$](img1064.gif)
Lema 1
(Osnovna lema)
Neka je skalarna funkcija
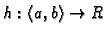
neprekidna na
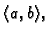
i neka je
za svaki par brojeva
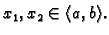
Tada je 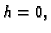 tj.
tj. 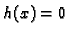 za svaki
za svaki
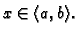
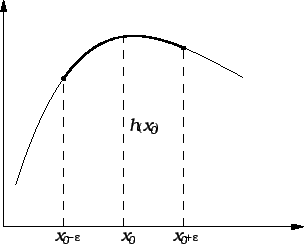
Dokaz. Pretpostavimo suprotno, da
postoji 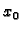 takav da je
takav da je 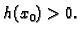 (Slično ide dokaz uz
pretpostavku
(Slično ide dokaz uz
pretpostavku 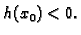 ) Zbog neprekidnosti funkcije
) Zbog neprekidnosti funkcije 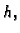 postoji
postoji
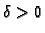 takav da
takav da
To
znači da je 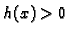 za
za
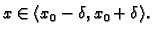 Ako izaberemo
Ako izaberemo
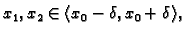 onda
je
što je u kontradikciji s
pretpostavkom u teoremu.
onda
je
što je u kontradikciji s
pretpostavkom u teoremu.
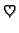
Podintegralna funkcija
je
vektorska. Iščezavanje njezinog integrala na proizvoljnom segmentu
![$ [x_1,x_2]$](img1084.gif) povlači iščezavanje integrala svake skalarne komponente
na tom segmentu. To, prema osnovnoj lemi povlači da je svaka skalarna
komponenta nulfunkcija. Slijedi
povlači iščezavanje integrala svake skalarne komponente
na tom segmentu. To, prema osnovnoj lemi povlači da je svaka skalarna
komponenta nulfunkcija. Slijedi
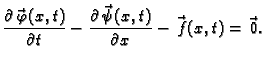 |
(2.1) |
Ova jednadžba predstavlja zakon održanja količine gibanja u
diferencijalnom obliku.
Ovo je opća jednadžba koja vrijedi za bilo kako napetu žicu od bilo kakvog
materijala. Karakteristike materijala i način na koji je žica napeta
opisuju se vezama između gore navedenih vektorskih polja. Te veze
se zovu zakoni ponašanja.
Zakoni ponašanja
Označimo s 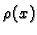 linearnu gustoću mase žice u točki
linearnu gustoću mase žice u točki 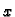 u čas
u čas
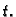 Linearna gustoća mase je masa po jedinici duljine. Tada je
količina gibanja po jedinici duljine u točki
Linearna gustoća mase je masa po jedinici duljine. Tada je
količina gibanja po jedinici duljine u točki 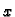 u čas
u čas 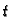 jednaka
umnošku mase po jedinici duljine u točki
jednaka
umnošku mase po jedinici duljine u točki 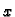 i brzine u točki
i brzine u točki 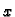 u
čas
u
čas 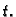 Tako imamo prvi zakon ponašanja
Tako imamo prvi zakon ponašanja
Usvojimo sada sljedeća pojednostavljenja.
Pretpostavljamo da se gibanje odvija u ravnini 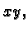 i to tako da je
i to tako da je
tj. tako da je komponenta
progiba u smjeru osi 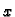 jednaka nuli. U skladu s ovom pretpostavkom
možemo progib smatrati skalarnim poljem
jednaka nuli. U skladu s ovom pretpostavkom
možemo progib smatrati skalarnim poljem 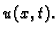
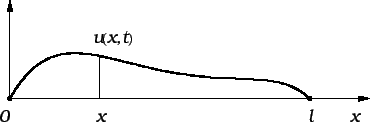
Promatrat ćemo male progibe žice, tako da možemo pretpostaviti da
je
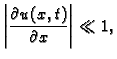
za svaki
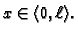
U tom
slučaju ćemo reći da je deformacija mala. Odatle
odnosno
To znači da je apsolutni
prirast progiba u odnosu na progib u ishodištu vrlo malen prema
duljini žice.
Slika 2.3:
Kontaktna sila pri malim deformacijama
Budući da je deformacija mala, možemo pretpostaviti da je kontaktna
sila
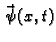 u točki
u točki 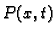 kolinearna s jediničnim
tangencijalnim vektorom na progib žice
kolinearna s jediničnim
tangencijalnim vektorom na progib žice 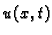 u točki
u točki 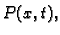 tj.
tj.
Funkcija 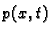 se zove
napetost žice u točki
se zove
napetost žice u točki 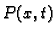 u čas
u čas 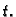 U daljnjem ćemo
pretpostavljati da napetost ne ovisi o vremenu, i da je u svakoj
točki pozitivna, tj. da je
U daljnjem ćemo
pretpostavljati da napetost ne ovisi o vremenu, i da je u svakoj
točki pozitivna, tj. da je
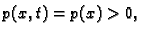
za svaki
![$\displaystyle x\in [0,\ell].$](img1103.gif)
Tako je
Progib
možemo shvatiti kao krivulju u ravnini s parametrizacijom
![$ ([0,\ell],\vec{\,r}),$](img1105.gif) gdje je
gdje je
Slika 2.4:
Progib kao krivulja u ravnini.
Tada je
Budući da je
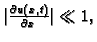 možemo zanemariti
možemo zanemariti
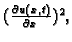 pa imamo
odnosno imamo drugi zakon ponašanja
pa imamo
odnosno imamo drugi zakon ponašanja
Vanjska sila po jedinici duljine djeluje u ravnini 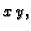 pa možemo
pisati
pa možemo
pisati
Slika 2.5:
Vanjska sila po jedinici duljine
Ako se s ovim vratimo u diferencijalnu jednadžbu (2.1), imamo
što se
raspada na dvije skalarne jednadžbe
Prva jednadžba omogućava izračunavanje napetosti žice. Da bi napetost bila neovisna o vremenu, nužno mora 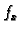 biti neovisno o vremenu. Tako imamo
biti neovisno o vremenu. Tako imamo
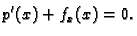 |
(2.2) |
Integrirajmo ovu jednadžbu
Ako vanjska sila
djeluje poprečno na žicu, onda je
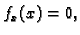 pa je
pa je
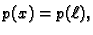 tj. napetost je konstantna, i jednaka napetosti na desnom
rubu. Ako vanjska sila ima komponentu u smjeru osi
tj. napetost je konstantna, i jednaka napetosti na desnom
rubu. Ako vanjska sila ima komponentu u smjeru osi 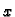 različitu od
nule, onda napetosti na desnom rubu treba dodati još doprinos od
vanjske sile po jedinici duljine.
različitu od
nule, onda napetosti na desnom rubu treba dodati još doprinos od
vanjske sile po jedinici duljine.
Druga jednadžba
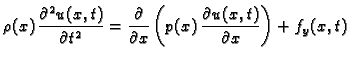 |
(2.3) |
se zove valna jednadžba. To je parcijalna diferencijalna
jednadžba. Napetost izračunamo iz prve jednadžbe, 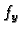 je zadano
time što je zadana vanjska sila po jedinici duljine.
je zadano
time što je zadana vanjska sila po jedinici duljine. 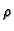 je
zadana linijska gustoća mase žice. Nepoznanica u jednadžbi je
progib
je
zadana linijska gustoća mase žice. Nepoznanica u jednadžbi je
progib 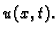 Osnovni problem je, dakle, izračunati
Osnovni problem je, dakle, izračunati 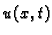 iz
valne jednadžbe. Ako pretpostavimo da je napetost konstantna duž
žice, valna jednadžba poprima oblik
Također
je prirodno pretpostaviti da je
iz
valne jednadžbe. Ako pretpostavimo da je napetost konstantna duž
žice, valna jednadžba poprima oblik
Također
je prirodno pretpostaviti da je
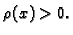 Tada možemo podijeliti
jednadžbu s
Tada možemo podijeliti
jednadžbu s 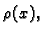 pa imamo
gdje je
pa imamo
gdje je 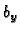 sila po jedinici duljine i po jedinici gustoće mase u
smjeru osi
sila po jedinici duljine i po jedinici gustoće mase u
smjeru osi 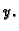 (U ovom slučaju to je akceleracija vanjske sile u
smjeru osi
(U ovom slučaju to je akceleracija vanjske sile u
smjeru osi 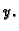 )
Ako žica oscilira u nekom sredstvu koje pruža otpor gibanju, onda
treba uzeti u obzir silu otpora. Budući da su oscilacije male,
može se pretpostaviti da sredstvo reagira kao elastično, tj. da
je sila otpora po jedinici duljine proporcionalna progibu i
suprotnog smjera
)
Ako žica oscilira u nekom sredstvu koje pruža otpor gibanju, onda
treba uzeti u obzir silu otpora. Budući da su oscilacije male,
može se pretpostaviti da sredstvo reagira kao elastično, tj. da
je sila otpora po jedinici duljine proporcionalna progibu i
suprotnog smjera
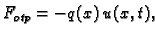 gdje je
gdje je
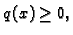 za
za
![$ x\in
[0,\ell]\,$](img1039.gif) faktor proporcionalnosti. U tom slučaju imamo
jednadžbu oscilacija
faktor proporcionalnosti. U tom slučaju imamo
jednadžbu oscilacija
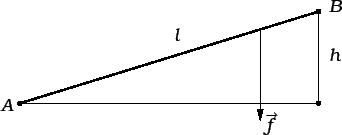
Primjer 2.1
Homogena teška žica, gustoće mase
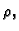
duljine
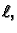
razapeta
je između točaka
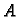
na zemlji i
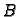
na visini
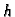
kao na slici.
Naći napetost žice u svakoj točki, ako je žica napeta u točki
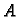
napetošću
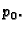
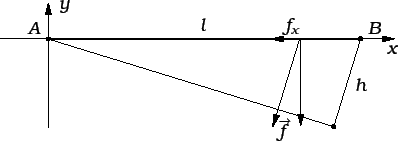
Rješenje. Kad kažemo teška žica, mislimo na to da se njezina težina ne
može zanemariti. To znači da na žicu djeluje vanjska sila, sila
teža. U izvodu jednadžbi mi smo koristili linearnu gustoću vanjske
sile (silu po jedinici duljine). Ona je ovdje u svakoj točki po
iznosu 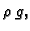 a po smjeru okomita je prema površini zemlje.
a po smjeru okomita je prema površini zemlje.
Postavimo koordinatni sustav tako da os 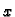 prolazi žicom. Gustoća
sile se može rastaviti na komponentu koja djeluje duž žice i onu
drugu koja je okomita na žicu. Napetosti pridonosi samo komponenta
duž žice.
prolazi žicom. Gustoća
sile se može rastaviti na komponentu koja djeluje duž žice i onu
drugu koja je okomita na žicu. Napetosti pridonosi samo komponenta
duž žice.
Iz slike vidimo (pomoću sličnosti trokuta) da je
Integrirajmo jednadžbu (
2.2) od 0 do
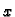
Ako žica nije homogena,
onda treba znati gustoću mase kao funkciju od

tj. tada
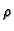
nije konstanta, već funkcija od

pa je tada
Primjer 2.2
Izvesti jednadžbu malih oscilacija napete žice u sredstvu s
otporom, koji je proporcionalan brzini.
Rješenje. Budući da se radi o malim oscilacijama, možemo usvojiti ona
pojednostavnjenja i zanemarivanja, koja smo usvojili kod izvoda
valne jednadžbe (
2.3). Dakle, možemo pretpostaviti da žica oscilira u smjeru okomitom na njezin ravnotežni položaj. U tom smjeru se javlja i sila otpora, no kako se ona opire kretanju, ona djeluje suprotno od smjera kretanja. Postavimo koordinatni sustav tako da žica u ravnoteži leži na osi
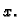
Tada se kretanje događa u smjeru osi
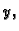
pa imamo jednadžbu za napetost
U smjeru osi
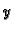
osim vanjske sile po jedinici duljine i kontaktne sile imamo još i silu otpora po jedinici duljine
Prema tome sada valna jednadžba glasi
odnosno
Ako vanjsko djelovanje ne ovisi o vremenu, ili ako se ono mijenja s
vremenom tako sporo da žica poprimi konačni položaj prije nego
se djelovanje izmijeni, onda je ustvari
tj.  ne ovisi o vremenu, i žica zauzima ravnotežni
položaj. Jednadžba ravnoteže žice je
ne ovisi o vremenu, i žica zauzima ravnotežni
položaj. Jednadžba ravnoteže žice je
Ako se žica nalazi u nekom sredstvu, onda je jednadžba ravnoteže
Jednadžbe ravnoteže su obične linearne diferencijalne jednadžbe
drugog reda, pa imaju beskonačno mnogo rješenja koja ovise o dvije
proizvoljno odabrane konstante. O uvjetima koje treba zadati da bismo
dobili rješenje u skladu s konkretnim problemom govorit ćemo
kasnije.
Primjer 2.3
Naći jednadžbu ravnote9nog položaja homogene teške žice,
gustoće mase
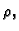
napete silom od
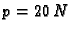
u polju sile teže,
koja djeluje okomito na žicu.
Rješenje. Jednadžba ravnoteže žice je
Pri tom je
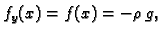
a
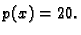
Prema tome jednadžba je
Sada ćemo bez izvoda dati matematičke modele za još neke
jednodimenzionalne fizikalne pojave.
Promatrat ćemo longitudinalne oscilacije grede koje nastaju
djelovanjem longitudinalne sile na gredu. Greda je kruto tijelo, pa
nije nužno da bude napeta da bi oscilirala. Budući da su sve sile,
pa i pomaci u smjeru središnje osi grede, koja neka bude os  vektorska polja možemo zamijeniti skalarnima. Imamo ova polja u vidu
vektorska polja možemo zamijeniti skalarnima. Imamo ova polja u vidu
-
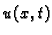 - longitudinalni pomak poprečnog presjeka grede u
točki
- longitudinalni pomak poprečnog presjeka grede u
točki 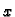 u čas
u čas 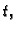
-
-
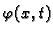 - ukupna
količina gibanja po jedinici duljine, u točki
- ukupna
količina gibanja po jedinici duljine, u točki  u čas
u čas 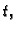
-
-
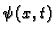 - količina gibanja, koja se kroz poprečni
presjek u točki
- količina gibanja, koja se kroz poprečni
presjek u točki  prenese u jedinici vremena s desna na lijevo u
čas
prenese u jedinici vremena s desna na lijevo u
čas 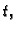
-
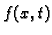 - količina gibanja po jedinici duljine, koja se u
jedinici vremena izvana prenese na gredu u točki
- količina gibanja po jedinici duljine, koja se u
jedinici vremena izvana prenese na gredu u točki  u
čas
u
čas 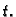
Prvi zakon ponašanja je isti kao kod žice
a drugi zakon ponašanja je zapravo Hookeov zakon
gdje je 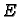 Youngov modul
elastičnosti, a
Youngov modul
elastičnosti, a 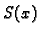 površina poprečnog presjeka grede. U ovom
slučaju je
pa imamo jednadžbu longitudinalnih
oscilacija grede
površina poprečnog presjeka grede. U ovom
slučaju je
pa imamo jednadžbu longitudinalnih
oscilacija grede
Jednadžba ravnoteže grede uslijed uzdužnog djelovanja vanjske sile
je
Torzijske oscilacije valjka
Pretpostavljamo da os valjka ostaje na miru, a da se poprečni
presjeci zakreću u svojoj ravnini. Imamo ova polja u vidu
-
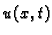 - kut zakreta poprečnog presjeka valjka u
točki
- kut zakreta poprečnog presjeka valjka u
točki 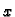 u čas
u čas 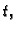
-
-
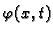 - zakretni moment po jedinici duljine valjka u
točki
- zakretni moment po jedinici duljine valjka u
točki  u čas
u čas 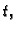
-
-
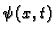 - zakretni moment, koji se u jedinici
vremena prenese s desna na lijevo kroz
poprečni presjek u točki
- zakretni moment, koji se u jedinici
vremena prenese s desna na lijevo kroz
poprečni presjek u točki  u čas
u čas 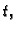
-
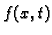 - zakretni moment po jedinici duljine, koji se u
jedinici vremena izvana prenese na gredu u točki
- zakretni moment po jedinici duljine, koji se u
jedinici vremena izvana prenese na gredu u točki  u
čas
u
čas 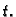
Zakretni moment također zadovoljava zakon održanja, pa na sličan
način kao kod oscilacija žice dolazimo do jednadžbe
Prvi zakon ponašanja
je u ovom slučaju formula koja opisuje zakretni moment pomoću kuta,
odnosno preciznije pomoću kutne brzine
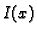 je
moment inercije poprečnog presjeka u odnosu na točku u kojoj os
valjka probada poprečni presjek.
je
moment inercije poprečnog presjeka u odnosu na točku u kojoj os
valjka probada poprečni presjek.
Drugi zakon ponašanja glasi
gdje je 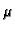 modul smicanja. Tako je
jednadžba torzijskih oscilacija valjka kružnog presjeka.
modul smicanja. Tako je
jednadžba torzijskih oscilacija valjka kružnog presjeka.
U slučaju valjka kružnog presjeka radiusa 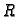 imamo
imamo
Provođenje topline kroz štap
Provođenje topline kroz štap je pojava koju ne vidimo. Informaciju o
provođenju topline dobivamo mjerenjem temperature. Temperaturu
mjerimo metrom, kao duljinu dužine. To nam omogućava fizikalna
pojava da se tijela prilikom zagrijavanja šire, pa ono što mi
mjerimo kao temperaturu je mjerenje duljine stupca žive u
termometru. Tako u vezi s provođenjem topline kroz štap imamo
sljedeća polja.
-
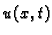 - temperatura poprečnog presjeka štapa u
točki
- temperatura poprečnog presjeka štapa u
točki 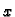 u čas
u čas 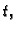
-
-
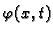 - ukupna
količina topline po jedinici duljine, u točki
- ukupna
količina topline po jedinici duljine, u točki  u čas
u čas 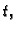
-
-
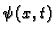 - količina topline, koja se u jedinici vremena
prenese s desna na lijevo kroz poprečni presjek u točki
- količina topline, koja se u jedinici vremena
prenese s desna na lijevo kroz poprečni presjek u točki  u
čas
u
čas 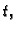
-
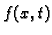 - količina topline po jedinici duljine, koja se u
jedinici vremena izvana prenese na gredu u točki
- količina topline po jedinici duljine, koja se u
jedinici vremena izvana prenese na gredu u točki  u
čas
u
čas 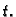
Toplina je jedan oblik energije, pa zadovoljava zakon o održanju
energije. Tako i u ovom slučaju vrijedi opća jednadžba
Zakoni ponašanja.
Količina topline po jedinici duljine štapa je proporcionalna
temperaturi
gdje je faktor
proporcionalnosti 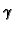 toplinski kapacitet jedinice duljine
štapa.
toplinski kapacitet jedinice duljine
štapa.
Drugi zakon ponašanja je poznat kao Fourierov zakon, koji kaže da je
količina topline koja u jedinici vremena prijeđe s desna na lijevo
proporcionalna razlici temperature po jedinici duljine
gdje je 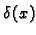 koeficijent provođenja. Iz ove formule slijedi da je
koeficijent provođenja. Iz ove formule slijedi da je
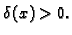
Ako sve to uzmemo u obzir, dobivamo iz opće jednadžbe
Primijetimo da je ova jednadžba drukčija od prethodnih po tome što
se ovdje pojavljuje prva parcijalna derivacija po 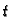 umjesto druge.
umjesto druge.
Filtracija kroz cijev
Cijev je ispunjena poroznom sredinom. Izvana nailazi određena masa
fluida, u cijevi se također nalazi neki fluid, pa nas interesira
kretanje fluida u takvim uvjetima kroz cijev. Ta pojava se zove
filtracija. Kretanje je moguće zato jer je sredina
porozna. Poroznost se mjeri omjerom volumena praznog prostora u
poroznoj sredini i ukupnog volumena porozne sredine. Taj omjer
označavamo s 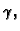 i zovemo ga poroznošću
materijala. Filtracija koja nas zanima događa se obično duboko pod
površinom zemlje (kretanje podzemnih voda, crpljenje nafte
utiskivanjem vode pod pritiskom u jednoj bušotini da bi se na drugoj
crpila), pa se proces
može mjeriti tako da spustimo sondu u cijev i da mjerimo tlak u
poprečnom presjeku cijevi. Tako imamo ova polja.
i zovemo ga poroznošću
materijala. Filtracija koja nas zanima događa se obično duboko pod
površinom zemlje (kretanje podzemnih voda, crpljenje nafte
utiskivanjem vode pod pritiskom u jednoj bušotini da bi se na drugoj
crpila), pa se proces
može mjeriti tako da spustimo sondu u cijev i da mjerimo tlak u
poprečnom presjeku cijevi. Tako imamo ova polja.
-
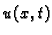 - tlak u poprečnom presjeku cijevi u točki
- tlak u poprečnom presjeku cijevi u točki 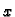 u čas
u čas 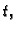
-
-
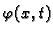 - ukupna masa fluida po jedinici duljine, u
točki
- ukupna masa fluida po jedinici duljine, u
točki  u čas
u čas 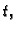
-
-
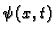 - masa fluida, koja se u jedinici vremena
prenese s desna na lijevo kroz poprečni presjek u točki
- masa fluida, koja se u jedinici vremena
prenese s desna na lijevo kroz poprečni presjek u točki  u
čas
u
čas 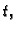
-
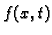 - masa fluida po jedinici duljine, koja se u
jedinici vremena izvana unese u cijev u točki
- masa fluida po jedinici duljine, koja se u
jedinici vremena izvana unese u cijev u točki  u
čas
u
čas 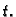
Budući da je ovdje u igri masa, i da vrijedi
zakon o održanju mase, i u ovom slučaju vrijedi opća jednadžba
Zakoni ponašanja.
Ako s 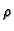 označimo linearnu gustoću fluida, imamo
označimo linearnu gustoću fluida, imamo
gdje je 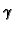 poroznost.
poroznost. 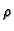 općenito ovisi o tlaku, no za različite fluide ta ovisnost je vrlo
različita. Na primjer imamo nestlačive fluide (voda, nafta), slabo
stlačive, pa do idealnih plinova kod kojih je
općenito ovisi o tlaku, no za različite fluide ta ovisnost je vrlo
različita. Na primjer imamo nestlačive fluide (voda, nafta), slabo
stlačive, pa do idealnih plinova kod kojih je
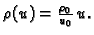
Drugi zakon kaže da je masa fluida koja po jedinici vremena prijeđe
s desna nalijevo proporcionalna razlici tlakova po jedinici duljine
gdje je
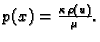 Ovdje je
Ovdje je 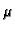 viskoznost
fluida, a
viskoznost
fluida, a 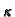 je permeabilnost (propustljivost) porozne
sredine. Ova formula je poznata kao Darcyjev zakon.
je permeabilnost (propustljivost) porozne
sredine. Ova formula je poznata kao Darcyjev zakon.
Jednadžba.
Uvrstimo li zakone ponašanja u opću jednadžbu, dobivamo
Bitna razlika u odnosu na jednadžbe kod prethodnih pojava je u tome
da je to nelinearna parcijalna diferencijalna jednadžba. Nelinearnost
se ogleda u tome da se  i njegove derivacije ne pojavljuju u
jednadžbi u linearnoj kombinaciji, već se pojavljuje i
i njegove derivacije ne pojavljuju u
jednadžbi u linearnoj kombinaciji, već se pojavljuje i 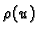 i
i
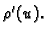 No u određenim slučajevima se jednadžba
pojednostavnjuje.
No u određenim slučajevima se jednadžba
pojednostavnjuje.
Nestlačivi fluid.
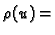 konst.
konst.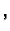 pa je
pa je
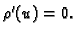 Tako imamo
Tako imamo
Ovdje se ne pojavljuje
derivacija po vremenu, što je odraz činjenice da se u
nestlačivom fluidu tlak prostire trenutno.
Slabo stlačiv fluid.
Kod slabo stlačivog fluida je
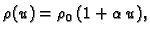 gdje
je
gdje
je 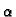 recipročna vrijednost prostornog modula
elastičnosti. Pri tom je
recipročna vrijednost prostornog modula
elastičnosti. Pri tom je
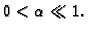 Tada je
Tada je
Kad se radi o malim promjenama polja
tlaka,
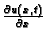 je mala veličina, pa se
je mala veličina, pa se
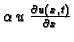 može zanemariti. Tako
imamo jednadžbu
može zanemariti. Tako
imamo jednadžbu
Idealni plin.
Kod idealnog plina je
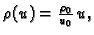 pa nakon
uvrštenja u jednadžbu imamo
pa nakon
uvrštenja u jednadžbu imamo
odnosno

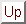



Next: Rubni problemi
Up: Rubni problemi
Previous: Rubni problemi
Contents
Index
Salih Suljagic
1999-12-17
![]() koje nastaje
uslijed nekog vanjskog djelovanja. Pretpostavit ćemo da vanjsko djelovanje
nije tako veliko da dolazi do plastičnih deformacija ili do kidanja
žice. Ako se progib ne mijenja s vremenom, onda govorimo o
ravnoteži žice. U protivnom govorimo o
oscilacijama žice.
koje nastaje
uslijed nekog vanjskog djelovanja. Pretpostavit ćemo da vanjsko djelovanje
nije tako veliko da dolazi do plastičnih deformacija ili do kidanja
žice. Ako se progib ne mijenja s vremenom, onda govorimo o
ravnoteži žice. U protivnom govorimo o
oscilacijama žice.
![]() s
vrijednostima u
s
vrijednostima u ![]() Prva varijabla je varijabla položaja
Prva varijabla je varijabla položaja
![]() a druga varijabla vremena
a druga varijabla vremena ![]()
![]() se zove kinematičko
polje, i ono opisuje progib žice. Ostala tri polja
se zove kinematičko
polje, i ono opisuje progib žice. Ostala tri polja
![]() se zovu dinamička
polja. Pri tom drugo vektorsko polje opisuje ukupnu količinu
gibanja. Treće vektorsko
polje opisuje količinu gibanja koja nastaje tako što se uslijed
neprekidnosti žice i njezine napetosti količina gibanja desnog
dijela žice preko točke
se zovu dinamička
polja. Pri tom drugo vektorsko polje opisuje ukupnu količinu
gibanja. Treće vektorsko
polje opisuje količinu gibanja koja nastaje tako što se uslijed
neprekidnosti žice i njezine napetosti količina gibanja desnog
dijela žice preko točke ![]() prenosi na lijevi dio. Četvrto vektorsko
polje opisuje količinu gibanja koja nastaje uslijed djelovanja
vanjske sile (gravitacija i sl.).
prenosi na lijevi dio. Četvrto vektorsko
polje opisuje količinu gibanja koja nastaje uslijed djelovanja
vanjske sile (gravitacija i sl.).
![]()
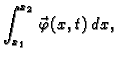
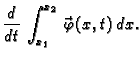
![]() u čas
u čas ![]() uslijed djelovanja vanjske sile je
uslijed djelovanja vanjske sile je
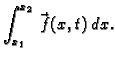
![]() u čas
u čas
![]() na desnom rubu, u točki
na desnom rubu, u točki ![]() je
je
![]() jednaka je zbroju
količina gibanja po jedinici vremena uslijed djelovanja preostalog
dijela žice i uslijed djelovanja vanjske sile. Dakle
jednaka je zbroju
količina gibanja po jedinici vremena uslijed djelovanja preostalog
dijela žice i uslijed djelovanja vanjske sile. Dakle
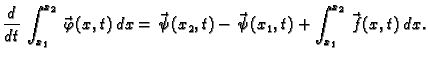
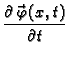
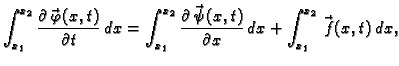
![$\displaystyle \int_{x_1}^{x_2}
\left[\frac{\partial\vec{\,\varphi}(x,t)}{\parti...
...\partial\vec{\,\psi}(x,t)}{\partial x} - \vec{\,f}(x,t)\right]\,dx =
\vec{\,0}.$](img1063.gif)
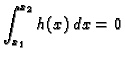
![]() tj.
tj. ![]() za svaki
za svaki
![]()
![]() takav da je
takav da je ![]() (Slično ide dokaz uz
pretpostavku
(Slično ide dokaz uz
pretpostavku ![]() ) Zbog neprekidnosti funkcije
) Zbog neprekidnosti funkcije ![]() postoji
postoji
![]() takav da
takav da
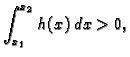
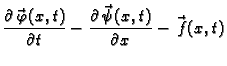
![]() linearnu gustoću mase žice u točki
linearnu gustoću mase žice u točki ![]() u čas
u čas
![]() Linearna gustoća mase je masa po jedinici duljine. Tada je
količina gibanja po jedinici duljine u točki
Linearna gustoća mase je masa po jedinici duljine. Tada je
količina gibanja po jedinici duljine u točki ![]() u čas
u čas ![]() jednaka
umnošku mase po jedinici duljine u točki
jednaka
umnošku mase po jedinici duljine u točki ![]() i brzine u točki
i brzine u točki ![]() u
čas
u
čas ![]() Tako imamo prvi zakon ponašanja
Tako imamo prvi zakon ponašanja
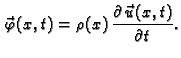
![]() i to tako da je
i to tako da je
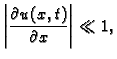 za svaki
za svaki 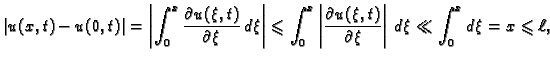
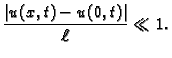
![]() u točki
u točki ![]() kolinearna s jediničnim
tangencijalnim vektorom na progib žice
kolinearna s jediničnim
tangencijalnim vektorom na progib žice ![]() u točki
u točki ![]() tj.
tj.
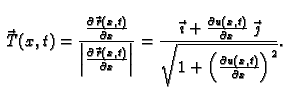
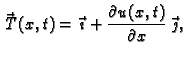
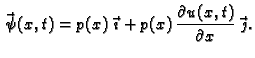
![]() pa možemo
pisati
pa možemo
pisati
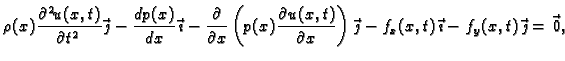
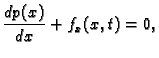
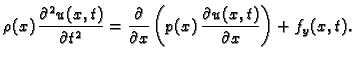
![]() biti neovisno o vremenu. Tako imamo
biti neovisno o vremenu. Tako imamo
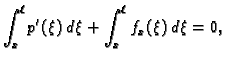
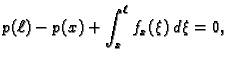
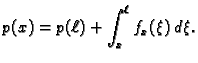
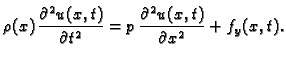
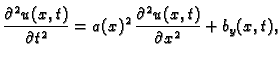
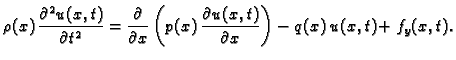
![]() a po smjeru okomita je prema površini zemlje.
a po smjeru okomita je prema površini zemlje.
![]() prolazi žicom. Gustoća
sile se može rastaviti na komponentu koja djeluje duž žice i onu
drugu koja je okomita na žicu. Napetosti pridonosi samo komponenta
duž žice.
prolazi žicom. Gustoća
sile se može rastaviti na komponentu koja djeluje duž žice i onu
drugu koja je okomita na žicu. Napetosti pridonosi samo komponenta
duž žice.
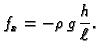
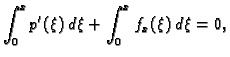
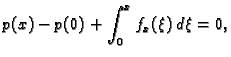
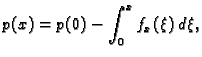
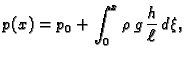
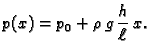
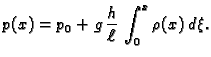
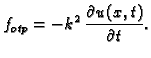
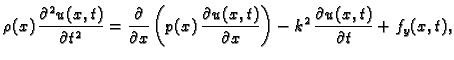
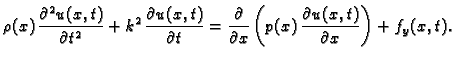
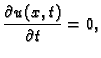

![]() vektorska polja možemo zamijeniti skalarnima. Imamo ova polja u vidu
vektorska polja možemo zamijeniti skalarnima. Imamo ova polja u vidu
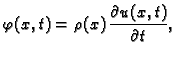
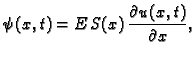
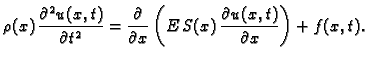
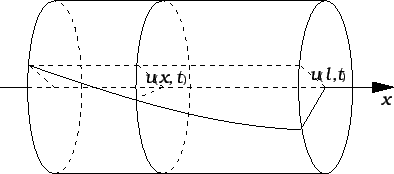
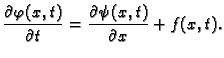
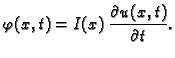
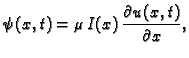
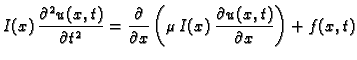
![]() imamo
imamo
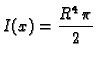
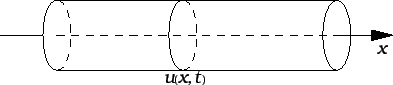
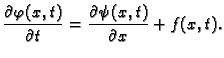
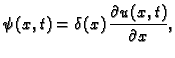
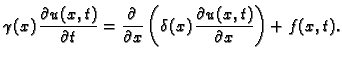
![]() umjesto druge.
umjesto druge.

![]() i zovemo ga poroznošću
materijala. Filtracija koja nas zanima događa se obično duboko pod
površinom zemlje (kretanje podzemnih voda, crpljenje nafte
utiskivanjem vode pod pritiskom u jednoj bušotini da bi se na drugoj
crpila), pa se proces
može mjeriti tako da spustimo sondu u cijev i da mjerimo tlak u
poprečnom presjeku cijevi. Tako imamo ova polja.
i zovemo ga poroznošću
materijala. Filtracija koja nas zanima događa se obično duboko pod
površinom zemlje (kretanje podzemnih voda, crpljenje nafte
utiskivanjem vode pod pritiskom u jednoj bušotini da bi se na drugoj
crpila), pa se proces
može mjeriti tako da spustimo sondu u cijev i da mjerimo tlak u
poprečnom presjeku cijevi. Tako imamo ova polja.
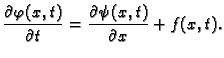
![]() označimo linearnu gustoću fluida, imamo
označimo linearnu gustoću fluida, imamo
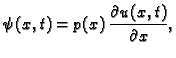
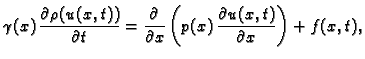
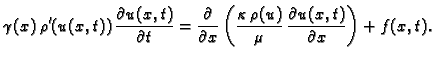
![]() i njegove derivacije ne pojavljuju u
jednadžbi u linearnoj kombinaciji, već se pojavljuje i
i njegove derivacije ne pojavljuju u
jednadžbi u linearnoj kombinaciji, već se pojavljuje i ![]() i
i
![]() No u određenim slučajevima se jednadžba
pojednostavnjuje.
No u određenim slučajevima se jednadžba
pojednostavnjuje.
![]() konst.
konst.![]() pa je
pa je
![]() Tako imamo
Tako imamo
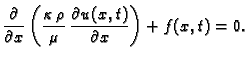
![]() gdje
je
gdje
je ![]() recipročna vrijednost prostornog modula
elastičnosti. Pri tom je
recipročna vrijednost prostornog modula
elastičnosti. Pri tom je
![]() Tada je
Tada je
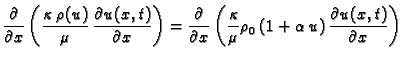
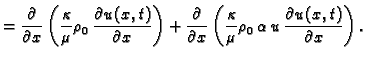
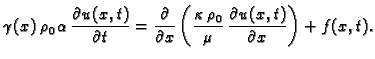
![]() pa nakon
uvrštenja u jednadžbu imamo
pa nakon
uvrštenja u jednadžbu imamo