| (3.1) |
Razmotrit ćemo nekoliko iterativnih postupaka za rješavanje jednadžbe
Metoda polovljenja se sastoji u tome da se segment ![]() na kojem je
ispunjen uvjet
na kojem je
ispunjen uvjet
![]() raspolovi, tj. nađe polovište
raspolovi, tj. nađe polovište ![]() Ako
je
Ako
je ![]() onda je
onda je ![]() U protivnom se ponovi operacija na onom od
segmenata
U protivnom se ponovi operacija na onom od
segmenata ![]() ili
ili ![]() na kojem je ispunjen uvjet
(3.2), itd. Tako imamo sljedeći algoritam.
na kojem je ispunjen uvjet
(3.2), itd. Tako imamo sljedeći algoritam.
Ovaj algoritam omogućava sljedeći program u programskom paketu 'Mathematica'.
f[t_]=; (* funkcija *)
a=;
b=; (* pocetni interval *)
x=(a+b)/2.;
n=0;
Print[{n,a,x,b}];
While[
N[f[x]]!=0.,
Print[" ",N[f[a]]," ",N[f[x]]," ",N[f[b]]];
If[
f[b]f[x]<0,
a=x;x=(x+b)/2,
b=x;x=(a+x)/2
];
n=n+1;
If[n>100,Break[] (* prekid petlje nakon 100 koraka *)
];
Print[{n,a,x,b}]]
Metoda uvijek konvergira, ali vrlo sporo. Očito je
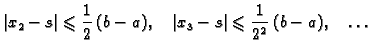
Rješenje. Računanjem vrijednosti polinoma
![]() na skupu
cijelih brojeva, dobivamo da je
na skupu
cijelih brojeva, dobivamo da je ![]() a
a ![]() Tako na
segmentu
Tako na
segmentu ![]() postoji bar jedno rješenje. Ako na ovaj problem
primijenimo gornji program, dobivamo sljedeću tablicu.
postoji bar jedno rješenje. Ako na ovaj problem
primijenimo gornji program, dobivamo sljedeću tablicu.
|
|
|
|||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
|
|||||
|
|
|
|
||||
|
|
|
|
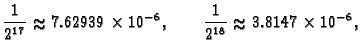
Zadatak iz primjera 3.1 se može doduše egzaktno riješiti pomoću Cardanovih formula. Ipak te formule nisu tako jednostavne kao formula za rješenje kvadratne jednadžbe, pa se algebarske jednadžbe trećeg stupnja često rješavaju približnim metodama. U sljedećem primjeru se rješava jednadžba koju ne možemo egzaktno riješiti.
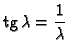
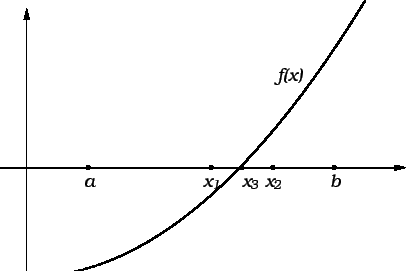
Rješenje. Iz slike 2.7 se vidi da se traženo rješenje nalazi
u intervalu
![]() Neka je
Neka je
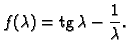
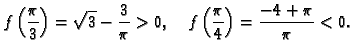
Izračunajmo sada koju aproksimaciju treba izračunati da bi se
dobila točnost na četiri decimale. Iz formule (3.3)
slijedi da treba naći ![]() tako da bude
tako da bude
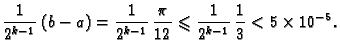
|
|
|
|||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
|
|||||
|
|
||||||
|
|
||||||
|
|
|
|||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
Napišimo jednadžbu (3.1) u obliku
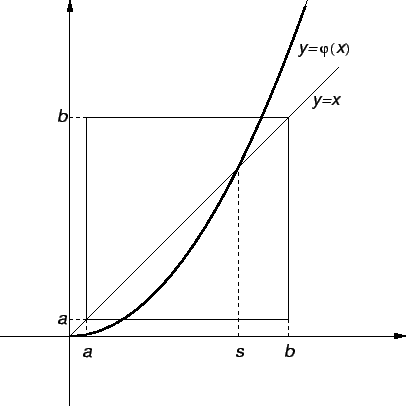
Imamo sljedeći algoritam
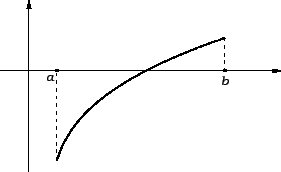
Ovaj algoritam dobro opisuje sljedeća slika.
Imamo sljedeći program za metodu iteracije
varphi[t_]=; (* funkcija *) x=; (* pocetna aproksimacija *) n=0; While[ N[f[x]]!=x, x=varphi[x]; n=n+1; If[n>100,Break[]]; (* prekid procesa nakon 100 iteracija *) Print[N[x]] ]
Može se dogoditi da ne postoji rješenje,
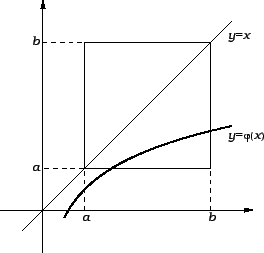
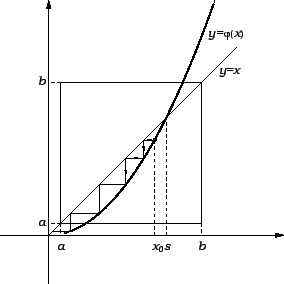
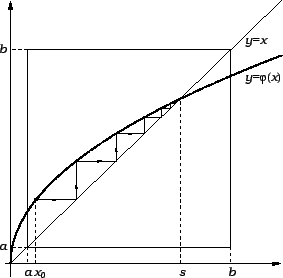
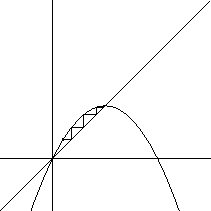

Da bi ova metoda funkcionirala, moraju brojevi
![]() biti u
biti u ![]() za bilo koju početnu
aproksimaciju. To će svakako biti ispunjeno, ako je
za bilo koju početnu
aproksimaciju. To će svakako biti ispunjeno, ako je
![]() A kako je funkcija
A kako je funkcija ![]() još i neprekidna, onda postoji bar jedna točka presjeka.
još i neprekidna, onda postoji bar jedna točka presjeka.
Tada za proizvoljan
![]() niz
niz ![]() definiran algoritmom (3.5) konvergira k jedinstvenom
rješenju jednadžbe
definiran algoritmom (3.5) konvergira k jedinstvenom
rješenju jednadžbe
![]()
Dokaz. Dokažimo najprije da postoji
barem jedno rješenje. Stavimo
![]() Prema uvjetima
teorema,
Prema uvjetima
teorema,
![]() i
i
![]() Budući da je
Budući da je
![]() neprekidna funkcija na segmentu
neprekidna funkcija na segmentu ![]() slijedi da postoji
bar jedan
slijedi da postoji
bar jedan
![]() takav da je
takav da je ![]() tj.
tj.
![]() dakle
dakle ![]() je rješenje.
je rješenje.
Dokažimo sada
da ne postoji više od jednog rješenja. Pretpostavimo da su ![]() i
i ![]() dva međusobno različita rješenja. Tada, prema
Lagrangeovom teoremu srednje vrijednosti,
dva međusobno različita rješenja. Tada, prema
Lagrangeovom teoremu srednje vrijednosti,
Apriornu ocjenu greške dobivamo na sljedeći način. Iz
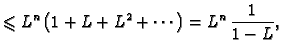
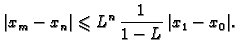
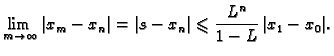
Aposteriorna ocjena greške je ocjena koja se računa pomoću dobivenih aproksimacija. U ovom slučaju ona je
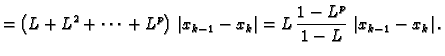
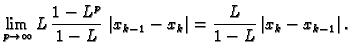
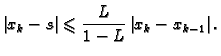
Rješenje. Iz
![$\displaystyle \varphi(x) = \sqrt[3]{x-1},\qquad \varphi'(x) = {\frac{1}{3\,{{\left(
x-1 \right) }^{{\frac{2}{3}}}}}}$](img2548.gif)
![$\displaystyle \varphi'(-1) = \frac{1}{3\,\sqrt[3]{4}} < \frac{1}{3}.$](img2552.gif)
![$\displaystyle L=\max_{x\in [-2,-1]}\vert\varphi'(x)\vert\leqslant{}\varphi'(-1)
\leqslant{}\frac{1}{3}$](img2553.gif)
Imamo na pr.
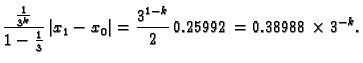
Rješenje. Jednadžbu treba napisati u obliku
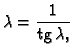
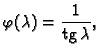
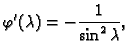
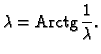
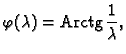
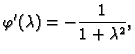
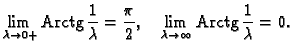
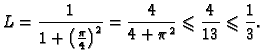
Neka je
![]() klase
klase ![]() na
na ![]() Želimo riješiti
jednadžbu
Želimo riješiti
jednadžbu
Newtonova metoda, koja se često zove
Newton-Raphsonova metoda ili metoda
tangente, sastoji se u tome da se ![]() -va
aproksimacija
-va
aproksimacija ![]() odredi kao sjecište tangente na graf funkcije
odredi kao sjecište tangente na graf funkcije ![]() u
točki s apscisom
u
točki s apscisom ![]() s osi
s osi ![]()
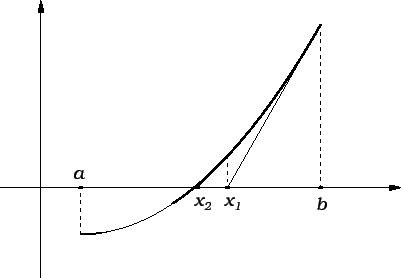
Jednadžba tangente na graf funkcije ![]() u točki
u točki
![]() je
je
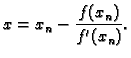
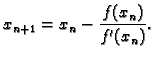
Time smo dobili sljedeći algoritam.
f[t_]=; (* funkcija *) x=; (* pocetna aproksimacija *) n=0; While[ N[f[x]]!=0., x=x-f[x]/f'[x]; n=n+1; If[n>100,Break[]]; (* prekid nakon 100 iteracija *) Print[N[x]] ]
Rješenje. Pomoću programa 3 s početnom aproksimacijom
![]() dobivamo
dobivamo
Rješenje. Pomoću programa 3 s početnom aproksimacijom
![]() dobivamo
dobivamo
S druge strane ako s istim programom (Newtonovom metodom) pokušamo riješiti jednadžbu
Tada Newtonova metoda konvergira k jedinstvenom rješenju jednadžbe ![]() za
bilo koju početnu aproksimaciju
za
bilo koju početnu aproksimaciju
![]()
Dokaz. Kombinirajući uvjete iz
teorema, mogli bismo promatrati razne slučajeve, no može se
pokazati da se svaki od njih, uzimajući ![]() umjesto
umjesto ![]() i/ili
i/ili
![]() umjesto
umjesto ![]() može svesti na slučaj
može svesti na slučaj
![$\displaystyle f(x) = f(\xi)+f'(\xi)\,(x-\xi)+\frac{f''(x_{\xi})}{2!}\,(x-\xi),\hspace{1cm}
\forall{}x\in[a,b],$](img2630.gif)
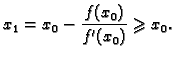
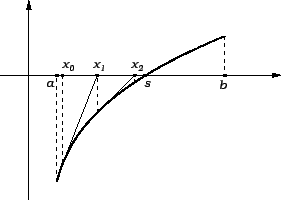
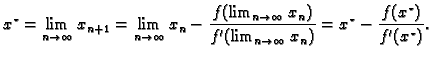
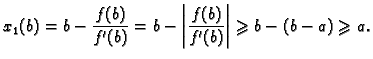
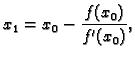
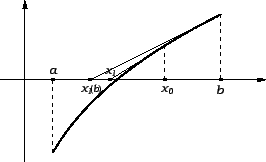
Rješenje. Izračunati ![]() -ti
korijen iz broja
-ti
korijen iz broja ![]() znači riješiti po
znači riješiti po ![]() jednadžbu
jednadžbu
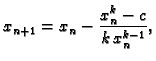
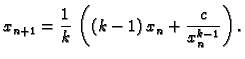
Što se tiče izbora početne aproksimacije ![]() i konvergencije,
primijetimo sljedeće. Za
i konvergencije,
primijetimo sljedeće. Za
![]() imamo
imamo
![]() Zatim, zbog
Zatim, zbog
![]()
![]() za svaki
za svaki
![]() je
je ![]() i
i ![]() Na kraju, iz pozitivnosti
funkcije
Na kraju, iz pozitivnosti
funkcije ![]() slijedi rast funkcije
slijedi rast funkcije ![]() pa je
pa je ![]() onaj rub segmenta
u kojem
onaj rub segmenta
u kojem ![]() ima manju vrijednost. Da bi vrijedilo
ima manju vrijednost. Da bi vrijedilo
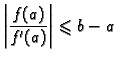
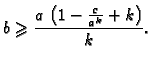
Specijalno kad je ![]() imamo formulu za približno računanje drugog
korijena
imamo formulu za približno računanje drugog
korijena
U programskom paketu Mathematica se ovaj postupak programira vrlo jednostavno
Map[Nest[((k-1) # + c/#^(k-1))/k&,x0,#1]&,Range[p]]//N
p broj aproksimacija koje želimo, a broj x0 je početna
aproksimacija. Naravno k je broj korijena koji se vadi.
Uvjerite se na primjerima kako je formula za računanje drugog korijena efikasna.
Rješenje. To je isto kao približno riješiti jednadžbu
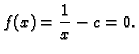
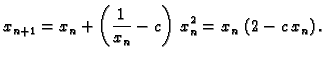
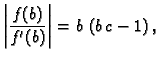
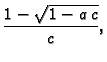 i
i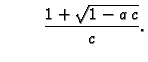
Ako želimo ocijeniti grešku, primijetimo da je Newtonova metoda zapravo metoda iteracije, ako stavimo
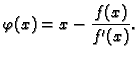
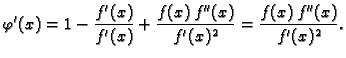
Neka je
![$\displaystyle \left\vert\frac{f(x)\,f''(x)}{f'(x)^2}\right\vert\leqslant L < 1,\hspace{1cm}\forall x\in
[a,b].$](img2695.gif)
Rješenje. Treba naći približnu vrijednost od ![]() Neka je
Neka je
![$\displaystyle L \leqslant{} \max{}\left\vert\frac{f(x)\,f''(x)}{f'(x)^2}\right\vert, \quad
\forall{}x\in [n,n+1].$](img2700.gif)
![$\displaystyle L \leqslant{} \max_{x\in [n,n+1]}\left\vert\frac{x^2-c}{2\,x^2}\r...
...ight\vert
\leqslant{} \frac{1}{2}\,\left\vert 1 - \frac{n}{(n+1)^2}\right\vert.$](img2702.gif)
Jedan od problema u Newtonovoj metodi je potreba računanja derivacije
u svakom koraku. Najjednostavniji način da se to izbjegne je da se
umjesto derivacije ![]() u formulu algoritma uvrsti konstanta
u formulu algoritma uvrsti konstanta
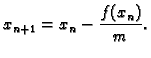
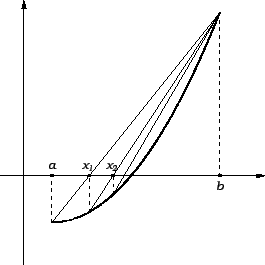
Ideja metode je da se ![]() -va aproksimacija odredi kao sjecište osi
-va aproksimacija odredi kao sjecište osi
![]() i sekante kroz točke na grafu funkcije
i sekante kroz točke na grafu funkcije ![]() čije apscise su
prethodne aproksimacije takve, da su vrijednosti funkcije u njima
različitog znaka. Dakle, možemo koristiti Newtonovu metodu u kojoj
čije apscise su
prethodne aproksimacije takve, da su vrijednosti funkcije u njima
različitog znaka. Dakle, možemo koristiti Newtonovu metodu u kojoj
![]() zamjenimo s koeficijentom sekante
zamjenimo s koeficijentom sekante
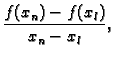
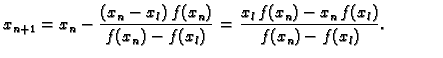
Tako imamo sljedeći algoritam.
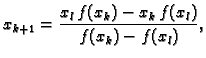
f[t_]=; (* funkcija *)
a=;
b=; (* pocetni interval (zadati kao realne brojeve) *)
If[f[a]f[b]<=0,
x=(a f[b]-b f[a])/(f[b]-f[a]);
n=0;
Print[{" ",n,N[a],N[x],N[b]}];
While[
N[f[x]]!=0.,
Print[N[f[a]]," ",N[f[x]]," ",N[f[b]]];
If[
f[b]f[x]<0,
a=x;x=N[(x f[b]-b f[x])/(f[b]-f[x])],
b=x;x=N[(a f[x]-x f[a])/(f[x]-f[a])]
];
n=n+1;
If[n>100,Break[]
];
Print[{" ",n,N[a],N[x],N[b]}]
],"Na odabranom segmentu nije ispunjen nuzan uvjet postojanja rjesenja
"]
Metoda uvijek konvergira. Konvergencija je brža nego kod metode polovljenja, ali sporija nego kod Newtonove metode.