Uvod

U dosadašnjem izlaganju smo matematički opisali razne probleme. Vidljivo je da su za rješavanje tih problema potrebna snažna matematička sredstva kao što su diferencijalne jednadžbe obične i parcijalne, integrali, algebarske jednadžbe, sustavi linearnih algebarskih jednadžbi itd. Želji da se na pr. rubni problem riješi egzaktno (točno) može biti udovoljeno samo ako su ulazni podaci toliko jednostavni da se potrebni postupci mogu izvesti točno i u relativno kratkom vremenu. Rijetko kada praktični problem ispunjava taj uvjet. Prema tome moramo se zadovoljiti traženjem približnog rješenja zadanog problema.

U matematici su razvijeni mnogi postupci približnog računanja. Ti postupci se zovu numerički postupci, a odgovarajuće područje matematike numerička matematika.

Greške

Prilikom numeričkog (približnog) rješavanja nastaju greške. Možemo ih podijeliti u tri kategorije.

1.

greške matematičkog modela,

2.

greške metode,

3.

greške računanja.

Greške matematičkog modela.

Do valne jednadžbe za oscilacije žice došli smo zanemarivanjem nekih veličina, i time već na početku uveli grešku, koja se kasnijim postupcima ne može ispraviti. Također, ulazni podaci kao što su duljina žice, vanjske sile, početni položaj, početna brzina nisu potpuno točni, jer su oni rezultat nekih mjerenja.

Greške metode.

Metoda kojom rješavamo problem može sadržavati beskonačnu sumaciju, računanje neelementarnih integrala, rješavanje algebarskih jednadžbi višeg reda itd. Na pr. kod Fourierove metode smo rješenje pretpostavljali u obliku beskonačne sume funkcija $u_n(P,t).$ U takvim slučajevima možemo izračunati samo neku parcijalnu sumu reda. Time činimo grešku.

Greške računanja.

Složeni problemi se rješavaju pomoću kompjutera. Kompjuter može samo konačno mnogo brojeva prikazati točno. Nazovimo te brojeve kompjuterski brojevi. Ako broj koji unosimo u kompjuter, ili s kojim on mora u nekom međukoraku baratati, nije kompjuterski, onda ga kompjuter zaokružuje, i time čini grešku. Jednostavniji proračun možemo izvršiti i bez kompjutera, no i tada, ako želimo dobiti ispis rezultata pomoću znamenki, moramo brojeve kao što su $\pi,e,\ldots$ zamijeniti približnim vrijednostima.

Da bismo se mogli pouzdati u rezultat nekog proračuna, moramo biti u stanju kontrolirati grešku. Recimo sada nešto o greškama i o tome kako se one ponašaju prilikom izvođenja operacija.

Neka je $a$ točna vrijednost nekog broja, i $a'$ njegova približna vrijednost. Kažemo da $a'$ aproksimira $a.$ Broj

$$\vert a' - a\vert$$

zovemo apsolutnom greškom, a broj

$$\frac{\vert a' - a\vert}{\vert a'\vert}$$

zovemo relativnom greškom aproksimacije.

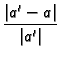
Kažemo da je $a'\approx{}a$ s točnošću $\epsilon{}$, ako je

$$\vert a' - a\vert \leqslant{} \epsilon{}.$$

Teorem 22   Neka je $a'\approx{}a$ s točnošću $\epsilon{}_1,$ i $b'\approx{}b$ s točnošću $\epsilon{}_2.$ Tada je

1.

$a'\pm b' \approx{} a\pm b$ s točnošću $\epsilon{}_1 + \epsilon{}_2,$

2.

$a'\,b' \approx{} a\,b$ s točnošću $\epsilon{}_1\,\vert b'\vert + \epsilon{}_2\,\vert a'\vert + \epsilon{}_1\,\epsilon{}_2,$

3.

$\frac{a'}{b'} \approx{} \frac{a}{b}$ s točnošću $\frac{\epsilon{}_1\,\vert b'\vert + \epsilon{}_2\,\vert a'\vert}{(\vert b'\vert - \epsilon{}_2)\,\vert b'\vert}.$

Dokaz. $\heartsuit$