




Next: Vlastite vrijednosti i vlastiti
Up: Problem vlastitih ...
Previous: Hamilton-Cayleyev teorem za simetrične
Sadržaj
Indeks
Ortogonalne matrice
Pogledajmo kako djeluje ortogonalna matrica 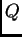 na prostoru
na prostoru
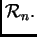 Iz
Iz
slijedi da 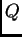 čuva skalarni produkt. Ako
stavimo
čuva skalarni produkt. Ako
stavimo
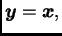 dobivamo
odakle
tj. ortogonalna matrica čuva duljinu vektora. Također
pa prema tome ortogonalna matrica čuva i kuteve do na predznak, jer
je kosinus kao parna funkcija neosjetljiv na predznak.
dobivamo
odakle
tj. ortogonalna matrica čuva duljinu vektora. Također
pa prema tome ortogonalna matrica čuva i kuteve do na predznak, jer
je kosinus kao parna funkcija neosjetljiv na predznak.
Budući da je 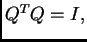 ortogonalna matrica je regularna i
ortogonalna matrica je regularna i
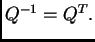 Nadalje, iz svojstava determinante (Binet-Cauchyjevog
teorema) slijedi
Nadalje, iz svojstava determinante (Binet-Cauchyjevog
teorema) slijedi
Prema tome je
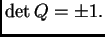
Subsections
2001-10-26
![]() na prostoru
na prostoru
![]() Iz
Iz
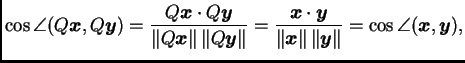
![]() ortogonalna matrica je regularna i
ortogonalna matrica je regularna i
![]() Nadalje, iz svojstava determinante (Binet-Cauchyjevog
teorema) slijedi
Nadalje, iz svojstava determinante (Binet-Cauchyjevog
teorema) slijedi