




Next: 1. slučaj.
Up: Ortogonalne matrice
Previous: Vlastite vrijednosti i vlastiti
Sadržaj
Indeks
Ortogonalne matrice drugog reda
Ortogonalne matrice drugog reda možemo shvatiti kao funkcije (linearne
operatore) koje preslikavaju
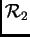 u
u
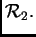 Neka je
Neka je
proizvoljna ortogonalna matrica drugog reda. Ona preslikava kanonsku
bazu u svoje stupce.
Prema tome stupci su međusobno okomiti, i njihova duljina jednaka je
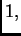 pa se pripadne točke nalaze na jediničnoj kružnici.
pa se pripadne točke nalaze na jediničnoj kružnici.
Uočimo prvi od njih. Prema upravo rečenom, postoji
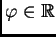 takav da je
takav da je
Slika 1.20:
Djelovanje ortogonalne matrice u ravnini.
|
|
Budući da je drugi stupac okomit na prvi, pripadna točka se nalazi
na jediničnoj kružnici na pravcu okomitom na radijvektor koji
pripada prvom stupcu. Takvih točaka imamo dvije, kao što se vidi na
sl. 1.20.
Subsections
2001-10-26
![]() u
u
![]() Neka je
Neka je
![% latex2html id marker 32489
$\displaystyle Q=\left[ \begin{array}{cc}
q_{11} & q_{12} \\
q_{21} & q_{22}
\end{array} \right]$](img747.png)
![% latex2html id marker 32491
$\displaystyle \left[ \begin{array}{cc}
q_{11} & q...
...{array} \right]=\left[ \begin{array}{c}
q_{12} \\ q_{22}
\end{array} \right]$](img748.png)
![]() takav da je
takav da je