Next: 2. slučaj.
Up: Ortogonalne matrice drugog reda
Previous: Ortogonalne matrice drugog reda
Sadržaj
Indeks
1. slučaj.
Radijvektor koji pripada točki zatvara kut
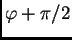 prema
pozitivnom dijelu osi
prema
pozitivnom dijelu osi 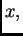 i prema tome
i prema tome
Tako imamo matricu
koja predstavlja rotaciju u ravnini oko
ishodišta za kut 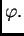
U ovom slučaju je očito 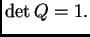
Nadalje
To je kvadratna jednadžba koja nema realnih rješenja, osim u
slučajevima kad je 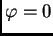 ili
ili
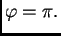 U tim slučajevima
rotacija je identično preslikavanje ili simetrija u odnosu na
ishodište. Dakle, možemo zaključiti da rotacija u ravnini za kut
U tim slučajevima
rotacija je identično preslikavanje ili simetrija u odnosu na
ishodište. Dakle, možemo zaključiti da rotacija u ravnini za kut
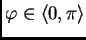 nema realnih vlastitih vektora, što je
geometrijski jasno.
nema realnih vlastitih vektora, što je
geometrijski jasno.
2001-10-26
![]() prema
pozitivnom dijelu osi
prema
pozitivnom dijelu osi ![]() i prema tome
i prema tome
![% latex2html id marker 32510
$\displaystyle Q=
\left[ \begin{array}{cc}
\cos {...
...& -\sin {\varphi } \\
\sin {\varphi } & \cos {\varphi }
\end{array} \right],$](img755.png)
![]()