




Next: Zaključak.
Up: Ortogonalne matrice drugog reda
Previous: 1. slučaj.
Sadržaj
Indeks
2. slučaj.
Radijvektor koji pripada točki zatvara kut
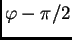 s
pozitivnim dijelom osi
s
pozitivnim dijelom osi 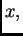 pa imamo
pa imamo
Matrica je sada
simetrična je, pa se može
dijagonalizirati. Karakteristična jednadžba je
Vlastite vrijednosti su
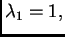
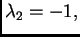 a vlastiti vektori su
Ako formiramo matricu
a vlastiti vektori su
Ako formiramo matricu 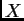 od ovih vektora, onda
je
U ovom slučaju se radi o simetriji u ravnini u odnosu na pravac čiji je
koeficijent smjera
od ovih vektora, onda
je
U ovom slučaju se radi o simetriji u ravnini u odnosu na pravac čiji je
koeficijent smjera
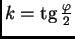 (sl. 1.21).
(sl. 1.21).
Slika 1.21:
Simetrija u ravnini.
|
|
U ovom slučaju je očito
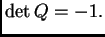
2001-10-26
![]() s
pozitivnim dijelom osi
s
pozitivnim dijelom osi ![]() pa imamo
pa imamo
![% latex2html id marker 32531
$\displaystyle Q=
\left[ \begin{array}{cc}
\cos {...
...& \sin {\varphi } \\
\sin {\varphi } & -\cos {\varphi }
\end{array} \right],$](img764.png)
![% latex2html id marker 32539
$\displaystyle \left[ \begin{array}{c}
\cos\frac{\...
...y}{c}
-\sin\frac{\varphi }{2} \\ \cos\frac{\varphi }{2}
\end{array} \right].$](img768.png)
![% latex2html id marker 32543
$\displaystyle X^{-1}Q\,X=\left[\begin{array}{cc}
1 & 0 \\
0 & -1
\end{array}\right]$](img769.png)
![]()