




Next: Ortogonalne matrice drugog reda
Up: Ortogonalne matrice
Previous: Ortogonalne matrice
Sadržaj
Indeks
Vlastite vrijednosti i vlastiti vektori
ortogonalnih matrica
Neka je 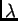 vlastita vrijednost, a
vlastita vrijednost, a
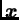 pripadni vlastiti vektor
ortogonalne matrice
pripadni vlastiti vektor
ortogonalne matrice 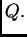 Tada je
Tada je
Konjugirajmo ovu
jednakost
Zbog svojstva
ortogonalnih matrica,
Budući da je
slijedi
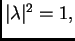 tj. kompleksan
broj
tj. kompleksan
broj 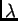 se nalazi na jediničnoj kružnici u Gaussovoj
ravnini. Specijalno, ako je
se nalazi na jediničnoj kružnici u Gaussovoj
ravnini. Specijalno, ako je 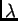 realan broj, onda je
realan broj, onda je 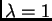 ili
ili
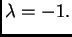
Pogledajmo sada što se može reći o ortogonalnim matricama drugog i
trećeg reda i o preslikavanjima koja one predstavljaju.
2001-10-26
![]() vlastita vrijednost, a
vlastita vrijednost, a
![]() pripadni vlastiti vektor
ortogonalne matrice
pripadni vlastiti vektor
ortogonalne matrice ![]() Tada je
Tada je