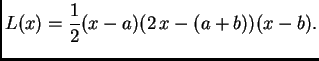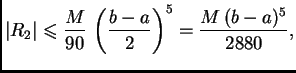Next: Trapezna formula
Up: Aproksimacija funkcije i numerička
Previous: Metoda najmanjih kvadrata
Sadržaj
Indeks
Numerička integracija
Zadatak je izračunati integral
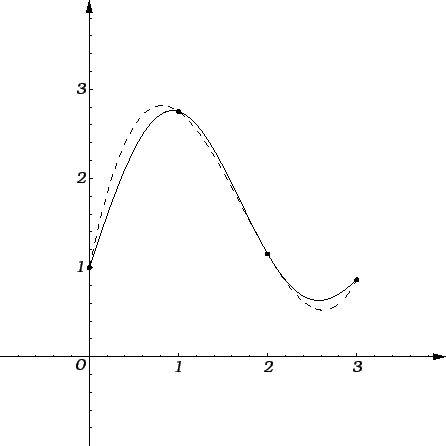
Umjesto da integriramo podintegralnu funkciju, što često nije
moguće, ili zahtijeva puno posla, integriramo polinom,
koji interpolira funkciju u odgovarajućim točkama.
Numerički to radimo na sljedeći način. Segment ![$ [a,b]$](img2579.png) podijelimo
na podsegmente točkama
Radi jednostavnosti i
određenosti postupka podjela se uzme ekvidistantnom. U tim točkama
interpoliramo funkciju Lagrangeovim polinomom, i zatim integriramo
polinom. Tako dobiven broj predstavlja približnu vrijednost zadanog
integrala. Dakle
Ako uvrstimo Lagrangeov polinom (3.14), imamo
podijelimo
na podsegmente točkama
Radi jednostavnosti i
određenosti postupka podjela se uzme ekvidistantnom. U tim točkama
interpoliramo funkciju Lagrangeovim polinomom, i zatim integriramo
polinom. Tako dobiven broj predstavlja približnu vrijednost zadanog
integrala. Dakle
Ako uvrstimo Lagrangeov polinom (3.14), imamo
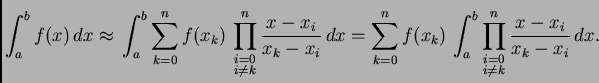 |
(3.19) |
Da bismo razmatranje učinili neovisnim o segmentu ![$ [a,b],$](img2352.png) svedimo
ga supstitucijom na fiksni segment
svedimo
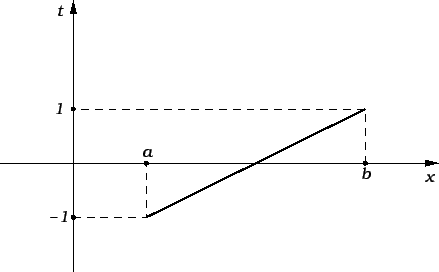
ga supstitucijom na fiksni segment ![$ [-1,1].$](img3017.png) To možemo učiniti
afinom funkcijom (polinomom prvog stupnja) čiji je graf pravac kroz
točke
To možemo učiniti
afinom funkcijom (polinomom prvog stupnja) čiji je graf pravac kroz
točke 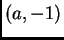 i
i 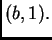 Jednadžba tog
pravca je
odnosno
Supstitucija čuva
ekvidistantnost, pa je
ekvidistantna podjela segmenta
Jednadžba tog
pravca je
odnosno
Supstitucija čuva
ekvidistantnost, pa je
ekvidistantna podjela segmenta ![$ [-1,1]$](img3024.png) na
na 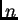 podsegmenata. Tom
supstitucijom formula (3.19) prelazi u
gdje je
podsegmenata. Tom
supstitucijom formula (3.19) prelazi u
gdje je
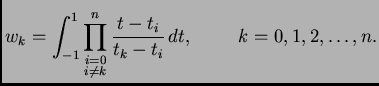 |
(3.20) |
Vidimo da ponderi 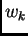 ne
ovise o segmentu
ne
ovise o segmentu ![$ [a,b],$](img2352.png) niti o funkciji, već samo o broju
niti o funkciji, već samo o broju 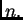
Iz formule (3.15) slijedi da je greška koju pri tom činimo
gdje je
Točka 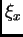 nam nije poznata, pa za ocjenu greške moramo uzeti
maksimum ove derivacije na segmentu
nam nije poznata, pa za ocjenu greške moramo uzeti
maksimum ove derivacije na segmentu ![$ [a,b]$](img2579.png) gdje je
gdje je
Specijalno za 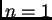 imamo
imamo
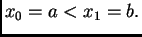 Zatim,
Zatim,
pa je
gdje je
Za 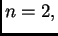 imamo tri točke podjele
imamo tri točke podjele
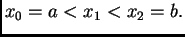 Pretpostavimo da
je podjela ekvidistantna, tj. da je
Pretpostavimo da
je podjela ekvidistantna, tj. da je
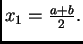 Tada je
Tada je
Kad bismo ponovili
postupak kao gore, dobili bismo u ocjeni 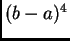 No, ta
se ocjena može poboljšati. Zbog činjenice da je funkcija
No, ta
se ocjena može poboljšati. Zbog činjenice da je funkcija 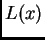 simetrična u odnosu na točku
simetrična u odnosu na točku
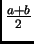 (graf je neparan u odnosu na tu točku), njezin integral po
segmentu
(graf je neparan u odnosu na tu točku), njezin integral po
segmentu ![$ [a,b]$](img2579.png) iščezava. U tom slučaju se funkcija može
interpolirati s polinomom 4. stupnja, tako da se točka
iščezava. U tom slučaju se funkcija može
interpolirati s polinomom 4. stupnja, tako da se točka
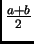 uzme kao dvostruka. O tome kako se to radi ovdje
nećemo govoriti. Primijetimo samo da se zbog integriranja polinoma 4.
stupnja u ocjeni pojavi
uzme kao dvostruka. O tome kako se to radi ovdje
nećemo govoriti. Primijetimo samo da se zbog integriranja polinoma 4.
stupnja u ocjeni pojavi 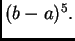 Može se pokazati de
je ona
gdje je
Može se pokazati de
je ona
gdje je
Subsections





Next: Trapezna formula
Up: Aproksimacija funkcije i numerička
Previous: Metoda najmanjih kvadrata
Sadržaj
Indeks
2001-10-26
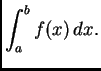
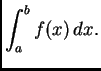
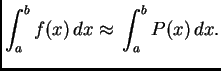
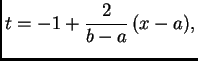
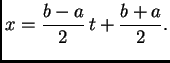
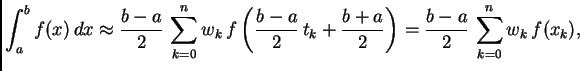
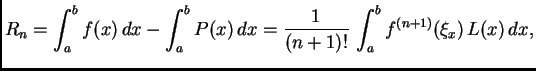
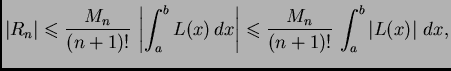
![]() imamo
imamo
![]() Zatim,
Zatim,
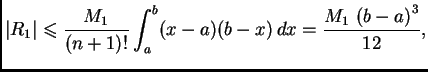
![]() imamo tri točke podjele
imamo tri točke podjele
![]() Pretpostavimo da
je podjela ekvidistantna, tj. da je
Pretpostavimo da
je podjela ekvidistantna, tj. da je
![]() Tada je
Tada je