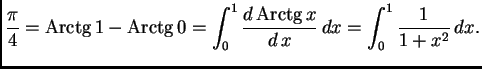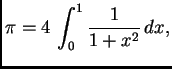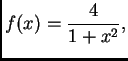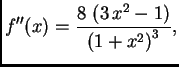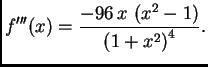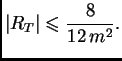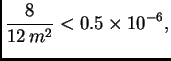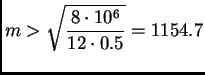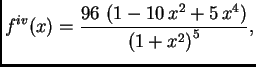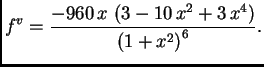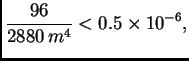Primjer 3.16
Pomoću numeričke integracije izračunati približno broj
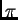
na
šest decimala točno.
Rješenje. Najprije sjetimo se da je
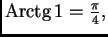 i
i 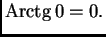 Odatle
Odatle
Dakle
pa treba izračunati ovaj
integral na šest decimala točno. Račun ćemo provesti na dva
načina, pomoću trapezne i pomoću Simpsonove formule.
1. Podintegralna funkcija je
njezina druga derivacija je
a treća
Kako treća derivacija nema nula u
intervalu
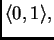
druga derivacija je na tom intervalu
monotona. Računanjem vrijednosti na rubovima lako se vidi da ona raste
i to od
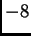
do
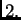
To znači da je
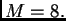
Dakle imamo ocjenu greške
za trapeznu formulu
Budući da tražimo točnost prvih šest decimala, mora biti
tj.
Prema tome treba segment
![$ [0,1]$](img3091.png)
podijeliti na
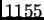
podsegmenata.
2. Pomoću Simpsonove formule račun ide ovako. Četvrta derivacija je
a peta
Peta derivacija se
poništava u
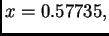
ali je
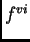
u toj točki pozitivna, pa
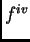
ima u
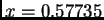
minimum. Tako četvrta derivacija pada na intervalu od 0 do
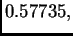
i zatim raste na intervalu od
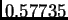
do
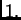
Imamo
Dakle
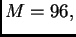
i prema tome treba biti
odakle
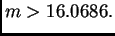
Budući da je broj segmenata potreban za Simpsonovu formulu paran, minimalni
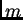
koji treba uzeti je
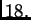
Kad se provede potreban račun dobije se
![]() iz formule (3.20) imamo
iz formule (3.20) imamo
![]() pa su ponderi
pa su ponderi
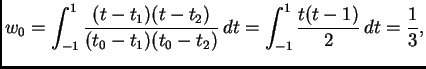
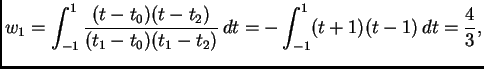
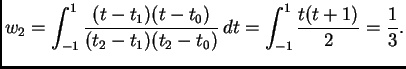
![% latex2html id marker 39821
$\displaystyle \int_a^b f(x)\,dx \approx{} \frac{b-a}{6}\,\left[f(a) +
4\, f\left(\frac{a+b}{2}\right) + f(b)\right],$](img3064.png)
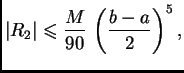
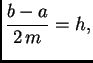 i
i ![% latex2html id marker 39835
$\displaystyle \int_a^b f(x)\,dx \approx{} \frac{b-a}{6\,m}\,\left[f(a) +
4\, f(x_1) + f(x_2)\right]+$](img3070.png)
![$\displaystyle + \frac{b-a}{6\,m}\,\left[f(x_2) +
4\, f(x_3) + f(x_4)\right] + \cdots{}+$](img3071.png)
![$\displaystyle +
\frac{b-a}{6\,m}\,\left[f(x_{2m-2}) +
4\, f(x_{2m-1}) + f(x_{b})\right],$](img3072.png)
![% latex2html id marker 39841
$\displaystyle \int_a^b f(x)\,dx\approx\frac{h}{3}\{f(a)+2\,[f(x_2)+f(x_4)+\cdots
+f(x_{2m-2})]$](img3073.png)
![$\displaystyle \vert R_S\vert \leqslant{} \max_{x \in [a,b]} \left\vert f^{iv}(x...
...x_{x \in [a,b]} \left\vert f^{iv}(x)\right\vert
\,\frac{(b-a)^5}{180\,(2m)^4}.$](img3076.png)
![]() i
i ![]() Odatle
Odatle