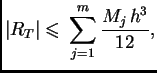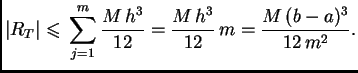Next: Simpsonova formula
Up: Numerička integracija
Previous: Numerička integracija
Sadržaj
Indeks
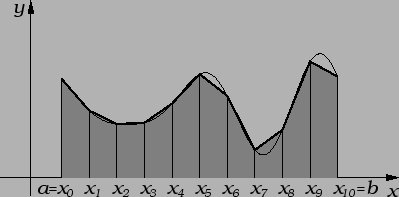
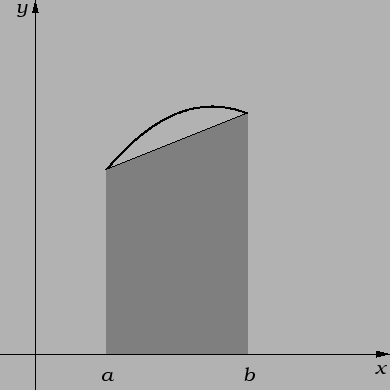
Trapezna formula
U slučaju 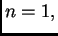 iz formule (3.20) imamo
iz formule (3.20) imamo
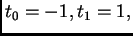 pa su ponderi
pa su ponderi
Prema tome formula glasi
![% latex2html id marker 39777
$\displaystyle \int_a^b f(x)\,dx \approx{} \frac{b-a}{2}\,\left[f(a)+f(b)\right],$](img3047.png) |
(3.21) |
uz ocjenu greške
Općenito je greška ove aproksimacije velika. Zato dijelimo segment
![$ [a,b]$](img2579.png) na podsegmente, i na svakom od njih posebno koristimo ovu
formulu. Radi jednostavnosti uzimamo ekvidistantnu podjelu. Neka je
dakle
na podsegmente, i na svakom od njih posebno koristimo ovu
formulu. Radi jednostavnosti uzimamo ekvidistantnu podjelu. Neka je
dakle
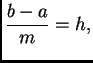
i
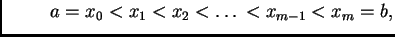
gdje je 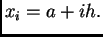 Ako na
svaki od podsegmenata, čija je duljina
Ako na
svaki od podsegmenata, čija je duljina 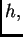 primijenimo formulu
(3.21), dobivamo
odnosno
primijenimo formulu
(3.21), dobivamo
odnosno
![% latex2html id marker 39793
$\displaystyle \int_a^b f(x)\,dx \approx{} \frac{h}...
...eft\{f(a)+2\,\left[f(x_1) + f(x_2) + \cdots{} + f(x_{m-1})\right]+f(b)\right\}.$](img3054.png) |
(3.22) |
Formula (3.22) se zove trapezna
formula.
Ocjena greške se dobije zbrajanjem grešaka na pojedinim
podsegmentima. Tako imamo
gdje je
Za ovu ocjenu trebalo bi mnogo puta (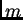 puta) ocjenjivati drugu
derivaciju i to na raznim podsegmentima, što nije jednostavno. Zato
radije ocjenu napravimo jednom za cijeli segment
puta) ocjenjivati drugu
derivaciju i to na raznim podsegmentima, što nije jednostavno. Zato
radije ocjenu napravimo jednom za cijeli segment ![$ [a,b],$](img2352.png) i uzmemo u
obzir da je za svaki
i uzmemo u
obzir da je za svaki 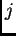 Tako imamo ocjenu
Tako imamo ocjenu





Next: Simpsonova formula
Up: Numerička integracija
Previous: Numerička integracija
Sadržaj
Indeks
2001-10-26
![]() iz formule (3.20) imamo
iz formule (3.20) imamo
![]() pa su ponderi
pa su ponderi
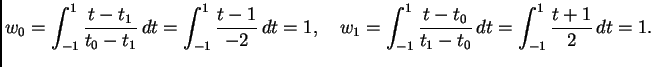
![$\displaystyle \vert R_1\vert \leqslant{} \max_{x \in [a,b]}
\left\vert f''(x)\right\vert\frac{(b-a)^3}{12}.$](img3048.png)
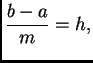 i
i ![% latex2html id marker 39791
$\displaystyle \int_a^b f(x)\,dx \approx{}
\frac{h}...
...ft[f(x_1)+f(x_2)\right] + \cdots{} +
\frac{h}{2}\,\left[f(x_{m-1})+f(b)\right],$](img3053.png)