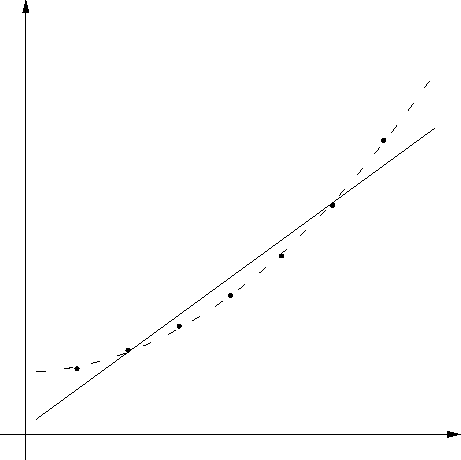
Na sljedećoj slici je funkcija, zadana svojim vrijednostima u nekoliko točaka (istaknute točke), interpolirana polinomom prvog stupnja (pravac) i polinomom drugog stupnja (crtkana linija) u smislu metode najmanjih kvadrata.

Lagrangeov polinom veoma dobro aproksimira funkciju lokalno, u izabranim točkama, dok izvan tih točaka aproksimacija može biti vrlo loša. Sada ćemo upoznati metodu najmanjih kvadrata, metodu pomoću koje možemo zadanu funkciju aproksimirati drugom funkcijom određenog tipa globalno, tako da u izvjesnom smislu njihova međusobna udaljenost bude što manja, bez obzira na to što se funkcije možda neće poklapati niti u jednoj točki.
Pretpostavimo najprije da su vrijednosti funkcije poznate samo u nekim
točkama. Neka su
![]() dane točke i neka su
dane točke i neka su
![]() pripadne vrijednosti funkcije
pripadne vrijednosti funkcije ![]() Želimo naći onu funkciju
Želimo naći onu funkciju ![]() određenog tipa s neodređenim
parametrima
određenog tipa s neodređenim
parametrima
![]() koja najbolje aproksimira
funkciju
koja najbolje aproksimira
funkciju ![]() To možemo učiniti na sljedeći način.
To možemo učiniti na sljedeći način.
Izračunamo sumu kvadrata razlika funkcija ![]() i
i ![]()
![$\displaystyle S = \sum_{k=1}^n \left[f(x_k) - g(x_k)\right]^2,$](img2976.png)
Ako je funkcija ![]() zadana u svim točkama nekog segmenta
zadana u svim točkama nekog segmenta ![]() onda se funkcija
onda se funkcija ![]() definira pomoću integrala
definira pomoću integrala
![$\displaystyle S = \int_{a}^b \left[f(x) - g(x)\right]^2\,dx.$](img2978.png)
Klase funkcija iz kojih biramo funkciju ![]() su obično polinomi prvog
stupnja
su obično polinomi prvog
stupnja
![]() polinomi drugog stupnja
polinomi drugog stupnja
![]() eksponencijalne funkcije
eksponencijalne funkcije
![]() itd.
itd.
Na pr. ako želimo naći polinom prvog stupnja najbliži funkciji
![]() čije su nam vrijednosti poznate u točkama
čije su nam vrijednosti poznate u točkama
![]() onda je
onda je
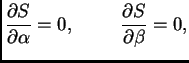
![$\displaystyle \sum_{k=1}^n \left[f(x_k) - \alpha{}\,x_k - \beta{}\right]\,x_k =
0,$](img2985.png)
![$\displaystyle \sum_{k=1}^n \left[f(x_k) - \alpha{}\,x_k - \beta{}\right] = 0.$](img2986.png)
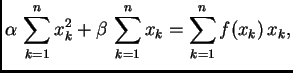
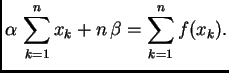
Kad se funkcija ![]() traži u obliku eksponencijalne, logaritamske i
slično, onda se na ovaj način u pravilu dobije sustav nelinearnih
jednadžbi. Takve sustave je teže rješavati nego linearne. Obično
se nekim operacijama nad funkcijama (na pr. logaritmiranjem)
pojednostavni klasa funkcija u kojoj tražimo aproksimaciju. No,
parametri koje tako dobijemo nisu najbolji mogući u smislu metode
najmanjih kvadrata.
traži u obliku eksponencijalne, logaritamske i
slično, onda se na ovaj način u pravilu dobije sustav nelinearnih
jednadžbi. Takve sustave je teže rješavati nego linearne. Obično
se nekim operacijama nad funkcijama (na pr. logaritmiranjem)
pojednostavni klasa funkcija u kojoj tražimo aproksimaciju. No,
parametri koje tako dobijemo nisu najbolji mogući u smislu metode
najmanjih kvadrata.
Rješenje. Neka je
![$\displaystyle S(a,b,c) = \sum_{k=1}^3 \left[f(x_k) -
c\,x^2 - b\,x_k - a\right]^2.$](img2996.png)
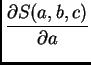 |
![$\displaystyle -2\,\sum_{k=1}^3 \left[f(x_k) -
c\,x^2 - b\,x_k - a\right] = 0$](img2998.png) |
||
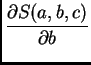 |
![$\displaystyle -2\,\sum_{k=1}^3 \left[f(x_k) -
c\,x^2 - b\,x_k - a\right]\,x_k = 0$](img3000.png) |
||
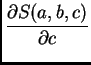 |
![$\displaystyle -2\,\sum_{k=1}^3 \left[f(x_k) -
c\,x^2 - b\,x_k - a\right]\,x_k^2 = 0.$](img3002.png) |