Neka je dana funkcija
![]() i međusobno različite
točke
i međusobno različite
točke ![]()
![]()
![]()
![]() u
u ![]() Želimo aproksimirati
funkciju
Želimo aproksimirati
funkciju ![]() polinomom koji u izabranim točkama ima iste vrijednosti
kao funkcija
polinomom koji u izabranim točkama ima iste vrijednosti
kao funkcija ![]() Ovako postavljen problem ima mnogo rješenja.
Međutim, ako zahtijevamo da stupanj polinoma bude najviše
Ovako postavljen problem ima mnogo rješenja.
Međutim, ako zahtijevamo da stupanj polinoma bude najviše ![]() onda
imamo samo jedno rješenje, što upravo tvrdi sljedeći teorem.
onda
imamo samo jedno rješenje, što upravo tvrdi sljedeći teorem.
Dokaz. Neka su polinomi
![]() stupnja najviše
stupnja najviše ![]() takvi da je
takvi da je
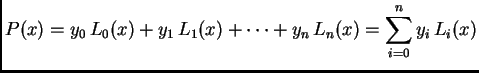
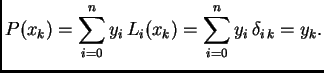
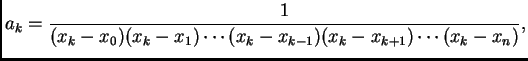
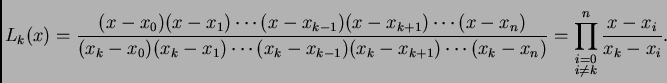
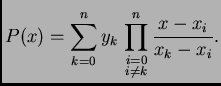
Polinom