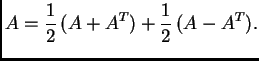Next: Determinanta
Up: Vektori i matrice
Previous: Linearna nezavisnost.
Sadržaj
Indeks
Definicija 3
U kvadratnoj matrici
![$ A=[a_{ij}]$](img37.png)
reda
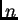
elementi
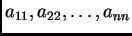
čine
glavnu
dijagonalu.
Zbroj elemenata na glavnoj dijagonali kvadratne matrice zovemo
trag
matrice i pišemo
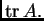 Dakle,
Dakle,
Kvadratne matrice imaju redaka koliko i stupaca, pa
se mogu množiti u bilo kojem poretku, no i u tom slučaju produkt nije
komutativan kao što pokazuje sljedeći primjer.
Definicija 4
Neka je
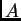
kvadratna matrica. Matrica
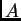
se zove
- -
- dijagonalna
matrica, ako je
![$ A=[a_{ij}\,\delta_{ij}],$](img109.png) tj. ako su joj
elementi izvan glavne dijagonale jednaki nuli,
tj. ako su joj
elementi izvan glavne dijagonale jednaki nuli,
- -
- skalarna
matrica, ako je
![$ A=[a\,\delta_{ij}],$](img110.png) tj. ako je dijagonalna i
ako su joj elementi na glavnoj dijagonali međusobno jednaki,
tj. ako je dijagonalna i
ako su joj elementi na glavnoj dijagonali međusobno jednaki,
- -
- gornja trokutasta, ako su joj
elementi ispod glavne dijagonale jednaki nuli,
- -
- donja trokutasta, ako su joj elementi iznad glavne
dijagonale jednaki nuli.
Skalarna matrica je dijagonalna, dok obrat naravno ne
vrijedi. Nulmatrica 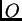 i jedinična matrica
i jedinična matrica 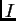 su skalarne
matrice. Dapače, svaka skalarna matrica ima oblik
su skalarne
matrice. Dapače, svaka skalarna matrica ima oblik
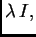 gdje je
gdje je 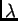 neki broj.
neki broj.
Budući da je 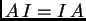 za svaku kvadratnu matricu
za svaku kvadratnu matricu 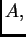 bilo koja
skalarna matrica komutira sa svakom matricom
bilo koja
skalarna matrica komutira sa svakom matricom
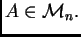
Elementi na glavnoj dijagonali
antisimetrične matrice su nule. Svaka kvadratna matrica se može na
jedinstven način razložiti na zbroj simetrične i antisimetrične
matrice:
Da je 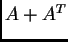 simetrična, a
simetrična, a 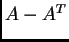 antisimetrična matrica, lako se
vidi upotrebom gornjih svojstava.1.1.1
antisimetrična matrica, lako se
vidi upotrebom gornjih svojstava.1.1.1
Subsections





Next: Determinanta
Up: Vektori i matrice
Previous: Linearna nezavisnost.
Sadržaj
Indeks
2001-10-26
![]() Dakle,
Dakle,
![]() Dakle,
Dakle,
![]() i jedinična matrica
i jedinična matrica ![]() su skalarne
matrice. Dapače, svaka skalarna matrica ima oblik
su skalarne
matrice. Dapače, svaka skalarna matrica ima oblik
![]() gdje je
gdje je ![]() neki broj.
neki broj.
![]() za svaku kvadratnu matricu
za svaku kvadratnu matricu ![]() bilo koja
skalarna matrica komutira sa svakom matricom
bilo koja
skalarna matrica komutira sa svakom matricom
![]()