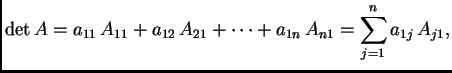
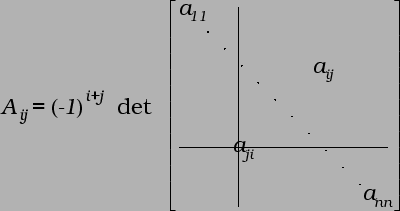
Broj ![]() se zove algebarski
komplement matričnog elementa
se zove algebarski
komplement matričnog elementa ![]()
Determinantu matrice reda ![]() ćemo kraće zvati
determinantom
ćemo kraće zvati
determinantom ![]() -tog reda.
-tog reda.
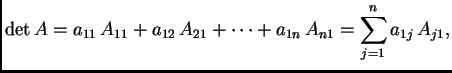

Broj ![]() se zove algebarski
komplement matričnog elementa
se zove algebarski
komplement matričnog elementa ![]()
Determinantu matrice reda ![]() ćemo kraće zvati
determinantom
ćemo kraće zvati
determinantom ![]() -tog reda.
-tog reda.
Ova definicija svodi računanje determinanti ![]() -tog reda na
računanje determinanti
-tog reda na
računanje determinanti ![]() -og reda, ovih opet po istoj formuli na
računanje determinanti
-og reda, ovih opet po istoj formuli na
računanje determinanti ![]() -og reda, itd. Tako dolazimo na kraju do
determinanti trećeg ili drugog reda koje znamo izračunati
-og reda, itd. Tako dolazimo na kraju do
determinanti trećeg ili drugog reda koje znamo izračunati

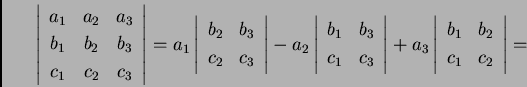
Računanje determinante po ovoj formuli je nepraktično, jer se s povećanjem reda jako povećava broj determinanti drugog ili trećeg reda koje treba izračunati. Zato ćemo navesti neka svojstva determinanti koja mogu bitno pojednostavniti njihovo računanje.