




Next: Vektori
Up: Inverzna matrica
Previous: Inverzna matrica
Sadržaj
Indeks
Svojstva skupa regularnih matrica.
- Produkt regularnih matrica je regularna matrica i vrijedi
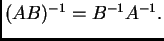
- Jedinična matrica
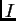 je regularna, i
je regularna, i 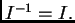
-
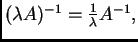 za svaki
za svaki
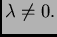
-
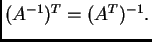
-
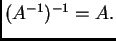
- Ako je
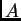 regularna matrica, onda je
regularna matrica, onda je
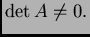
Nulmatrica množena s bilo kojom matricom daje nulmatricu,
pa tako ne postoji njezin inverz. Dakle, nulmatrica je singularna. No
to nije jedina singularna matrica kao što pokazuje sljedeći primjer.
Primjer 1.3
Matrica
nema inverznu.
Rješenje. Iz primjera 1.1 se vidi da je
Pretpostavimo da postoji inverz
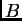
matrice
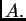
Tada je
S druge strane
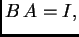
pa je
Slijedi
što je u kontradikciji s definicijom jednakosti matrica.
Može se dokazati da vrijedi
za svaki 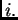 No, ako algebarske komplemente
elemenata jednog retka množimo s elementima drugog retka i zbrojimo,
dobivamo nulu
No, ako algebarske komplemente
elemenata jednog retka množimo s elementima drugog retka i zbrojimo,
dobivamo nulu
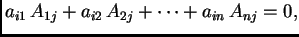
za
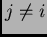
To slijedi odatle što je lijeva
strana jednaka determinanti u kojoj je umjesto 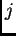 -tog retka napisan
-tog retka napisan
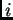 -ti. Tako u determinanti imamo dva retka jednaka, pa je ona jednaka
nuli. Dakle za svaki
-ti. Tako u determinanti imamo dva retka jednaka, pa je ona jednaka
nuli. Dakle za svaki 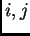 vrijedi
Na lijevoj strani ove jednakosti se nalazi
vrijedi
Na lijevoj strani ove jednakosti se nalazi 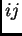 -ti element
produkta matrice
-ti element
produkta matrice
![$ A=[a_{ij}]$](img37.png) i matrice
i matrice
![$ B=[A_{ij}].$](img173.png) Vidimo da je
tj.
Odgovarajuće formule vrijede ako se uzmu stupci matrice
Vidimo da je
tj.
Odgovarajuće formule vrijede ako se uzmu stupci matrice 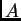 umjesto redaka, pa se može slično dobiti formula
Odavde je jasno da je
Matrica
umjesto redaka, pa se može slično dobiti formula
Odavde je jasno da je
Matrica
![$ B = [A_{ij}]$](img178.png) se zove adjunkta matrice
se zove adjunkta matrice
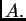
Na temelju ove diskusije može se zaključiti da vrijedi i obrat
6. svojstva skupa regularnih matrica 1.1.2, tj. da
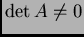 povlači regularnost matrice. Tako vrijedi
povlači regularnost matrice. Tako vrijedi
6'. Matrica 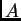 je regularna ako i samo ako je
je regularna ako i samo ako je
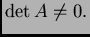





Next: Vektori
Up: Inverzna matrica
Previous: Inverzna matrica
Sadržaj
Indeks
2001-10-26
![% latex2html id marker 30396
$\displaystyle A=\left[\begin{array}{cc}
1 & 0 \\
0 & 0
\end{array}\right]$](img161.png)
![% latex2html id marker 30398
$\displaystyle A\,\left[\begin{array}{cc}
0 & 0 \\...
...nd{array}\right]=\left[\begin{array}{cc}
0 & 0 \\
0 & 0
\end{array}\right].$](img162.png)
![% latex2html id marker 30404
$\displaystyle (B\,A)\,\left[\begin{array}{cc}
0 &...
...nd{array}\right]=\left[\begin{array}{cc}
0 & 0 \\
0 & 0
\end{array}\right].$](img163.png)
![% latex2html id marker 30408
$\displaystyle (B\,A)\,\left[\begin{array}{cc}
0 &...
...nd{array}\right]=\left[\begin{array}{cc}
0 & 0 \\
0 & 1
\end{array}\right].$](img165.png)
![% latex2html id marker 30410
$\displaystyle \left[\begin{array}{cc}
0 & 0 \\
...
...nd{array}\right]=\left[\begin{array}{cc}
0 & 0 \\
0 & 0
\end{array}\right],$](img166.png)
![$\displaystyle A^{-1} = \frac{1}{\det
A}\,[A_{ij}].$](img177.png)
![]() povlači regularnost matrice. Tako vrijedi
povlači regularnost matrice. Tako vrijedi
![]() je regularna ako i samo ako je
je regularna ako i samo ako je
![]()