Vektori

Definicija 8   $n$-torku realnih brojeva

$$\boldsymbol{x}=\left[ \begin{array}{c} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{array} \right]$$

zovemo vektorstupcem, a

$$\boldsymbol{x}^{T}=\left[\begin{array}{cccc} x_{1} & x_{2} & \cdots & x_n \end{array} \right]$$

vektorretkom. Uglavnom ćemo raditi s vektorstupcima, pa ćemo njih jednostavno zvati vektorima. Kraće ćemo ih zapisivati

$$\boldsymbol{x}=[x_i].$$

Skup svih vektorstupaca ćemo označavati s ${\cal R}_{n},$ a svih vektorredaka s ${\cal R}^T_n.$

Kako je vektor $\boldsymbol{x}$ u ${\cal R}_{2}$ zadan s dva realna broja, od kojih se zna koji je prvi, a koji drugi, možemo $\boldsymbol{x}$ identificirati s uređenim parom realnih brojeva, dakle točkom u ravnini, a prema tome i s radijvektorom u ravnini.

Slika 1.1: Vektorstupac u ${\cal R}_{2}$ kao vektor u ravnini

Vektor $\boldsymbol{x}$ u ${\cal R}_{3}$ je zadan s tri realna broja, od kojih se zna koji je prvi, koji je drugi, a koji je treći. Tako možemo $\boldsymbol{x}$ identificirati s uređenom trojkom realnih brojeva, dakle točkom u prostoru, a prema tome i s radijvektorom u prostoru.

Slika 1.2: Vektorstupac u ${\cal R}_{3}$ kao vektor u prostoru

Kao što smo vidjeli ${\cal M}_{mn}$ je vektorski prostor. Tako su i ${\cal R}_{n}={\cal M}_{n1}$ i ${\cal R}^T_n={\cal M}_{1n}$ vektorski prostori.

Budući da su vektori ustvari jednostupčaste matrice, znamo ih zbrajati i množiti brojem. Također znamo što je vektor 0 i taj vektor zovemo nulvektorom.

Operacije, koje su dane u ${\cal R}_{n},$ omogućavaju da pravimo linearne kombinacije vektora. Neka su dani vektori $\boldsymbol{x}_1,\boldsymbol{x}_2,\ldots,\boldsymbol{x}_k\in{\cal R}_{n},$ i brojevi $\lambda_1,$ $\lambda_2,$ $\ldots,$ $\lambda_k.$ Linearnom kombinacijom vektora $\boldsymbol{x}_1,\boldsymbol{x}_2,\ldots,\boldsymbol{x}_k$ zovemo vektor

$$\lambda_1\,\boldsymbol{x}_1+\lambda_2\,\boldsymbol{x}_2+\cdots+\lambda_k\,\boldsymbol{x}_k.$$ (1.3)

Brojeve $\lambda_1,\lambda_2,\ldots,\lambda_k$ zovemo koeficijentima linearne kombinacije (1.3).

Definicija 9   Za vektore $\boldsymbol{x}_1,\boldsymbol{x}_2,\ldots,\boldsymbol{x}_k$ kažemo da su linearno nezavisni, ako

$$\lambda_1\,\boldsymbol{x}_1+\lambda_2\,\boldsymbol{x}_2+\cdots+\lambda_k\,\boldsymbol{x}_k=$$   0$$\hspace{3mm}\Rightarrow \hspace{3mm} \lambda_1=0,\lambda_2=0,\ldots,\lambda_k=0.$$

U protivnom kažemo da su linearno zavisni.

Primjer 1.4   Neka su dana tri vektora

$$\boldsymbol{x}_1=\left[ \begin{arra... ...uad \boldsymbol{x}_3=\left[ \begin{array}{r} -1 \\ -2 \end{array} \right].$$

Tada je

$$2\boldsymbol{x}_1+\frac{3}{2}\boldsymbol{x}_2 + \frac{5}{2}\boldsymbol{x}_3 = \textbf{0}.$$

Kako su koeficijenti u linearnoj kombinaciji različiti od $0,$ ti vektori su linearno zavisni.

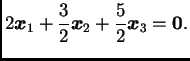
Na slici 1.3 su vektori u ravnini reprezentirani radijvektorima, i pokazano je kako linearna kombinacija iščezava.

Slika 1.3: Linearna zavisnost vektora

Pokušajte se uvjeriti crtežom da linearna kombinacija dva od njih, na pr. $\boldsymbol{x}_1,\boldsymbol{x}_2$ daje $\textbf{0}$ samo u slučaju da su koeficijenti linearne kombinacije jednaki $0.$

Primjer 1.5   Ispitati linearnu nezavisnost sljedećih vektora u odnosu na parametre $a$ i $b.$

$$\boldsymbol{x}_1 = \left[\begin{arra... ...ldsymbol{x}_4 = \left[\begin{array}{c} a \\ 1 \\ 0 \\ 5 \end{array}\right].$$

Rješenje. Jednakost

$$\lambda{}_1\,\boldsymbol{x}_1 + \lambda{}_2\,\boldsymbol{x}_2 + \lambda{}_3\,\boldsymbol{x}_3 + \lambda{}_4\,\boldsymbol{x}_4 = \textbf{0}$$

vodi na sustav jednadžbi

$$7 \,\lambda_2+b \,\lambda_3+a \,\lambda_4 =$$ 0

$$\,\lambda_1+4 \,\lambda_2+3 \,\lambda_3+\,\lambda_4 =$$ 0

$$\,\lambda_2 =$$ 0

$$2 \,\lambda_1+8 \,\lambda_2+4 \,\lambda_3+5 \,\lambda_4 = 0.$$

Slijedi $\lambda_2=0.$ Ostaju tri jednadžbe s tri nepoznanice. Eliminiramo nepoznanicu $\lambda_1.$ Ostaju dvije jednadžbe s nepoznanicama $\lambda_3$ i $\lambda_4.$

$$b \,\lambda_3+a \,\lambda_4 =$$ 0

$$-2 \,\lambda_3+ 3 \,\lambda_4 = 0.$$

Odatle dobivamo jednu jednadžbu

$$(3\,b + 2\,a)\,\lambda_4 = 0.$$

Ako je $3\,b + 2\,a \neq 0,$ onda je $\lambda{}_4=0,$ i zatim $\lambda{}_3=0,$ i kad se s tim vratimo u početni sustav dobivamo i $\lambda{}_1 =0.$ Dakle, za

$$a \neq -\frac{3}{2}\,b$$

vektori su linearno nezavisni.

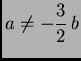
U protivnom, ako je

$$3\,b + 2\,a = 0,$$

onda $\lambda{}_4$ može biti proizvoljan broj, prema tome i različit od $0.$ Tako su, u tom slučaju, vektori linearno zavisni.