Skalarni produkt.

U ${\cal R}_{n}$ možemo definirati skalarni produkt na sljedeći način.

Definicija 10   Neka su $\boldsymbol{x}=\left[x_{i}\right]$ i $\boldsymbol{y}=\left[y_{i}\right]$ proizvoljni vektori u ${\cal R}_{n}.$ Skalarni produkt vektora $\boldsymbol{x}$ i $\boldsymbol{y}$ je broj (skalar)

$$\boldsymbol{x}\cdot\boldsymbol{y}=x_{1}\,y_{1}+x_{2}\,y_{2}+ \cdots +x_{n}\,y_{n}= \sum_{i=1}^n x_{i}\,y_{i}.$$

Vektore možemo shvatiti kao jednostupčaste matrice. U tom slučaju se skalarni produkt može zapisati kao

$$\boldsymbol{x}\cdot\boldsymbol{y}=\boldsymbol{y}^T\,\boldsymbol{x}=\boldsymbol{x}^T\,\boldsymbol{y}.$$

Skalarni produkt ima sljedeća svojstva.

1. $(\boldsymbol{x}+\boldsymbol{y})\cdot\boldsymbol{z}=\boldsymbol{x}\cdot\boldsymbol{z}+\boldsymbol{y}\cdot\boldsymbol{z},$
2. $(\lambda\,\boldsymbol{x})\cdot\boldsymbol{y}=\lambda\,(\boldsymbol{x}\cdot\boldsymbol{y}),$
3. $\boldsymbol{x}\cdot\boldsymbol{y}=\boldsymbol{y}\cdot\boldsymbol{x},$
4. $\boldsymbol{x}\cdot\boldsymbol{x}\geq 0,$
5. $\boldsymbol{x}\cdot\boldsymbol{x}=0$ ako i samo ako je $\boldsymbol{x}=\textbf{0}.$

U vektorskom prostoru radijvektora (usmjerenih dužina) smo pomoću skalarnog produkta računali duljine vektora, kuteve između njih, i prema tome rješavali određene geometrijske probleme. Koristeći skalarni produkt to možemo sada i u ${\cal R}_{n}.$ Tako kažemo da je duljina vektora $\boldsymbol{x}$

$$\Vert\boldsymbol{x}\Vert=\sqrt{\boldsymbol{x}\cdot\boldsymbol{x}}=\sqrt{\boldsymbol{x}^T\,\boldsymbol{x}}=\sqrt{\sum_{i=1}^n x_i^2},$$

a kut $\phi$ između vektora $\boldsymbol{x}$ i $\boldsymbol{y}$ se računa iz formule

$$\cos\phi=\frac{\boldsymbol{x}\cdot\boldsymbol{y}}{\Vert\boldsymbol{x}\Vert\,\Vert\boldsymbol{y}\Vert}.$$

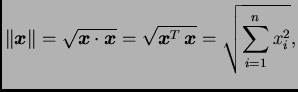
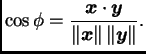
Pomoću skalarnog produkta vektora možemo kraće zapisati umnožak dvije matrice. Označimo s $\boldsymbol{a}_{i\cdot}$ $i$-ti redak matrice $A,$ a s $\boldsymbol{b}_{\cdot k}$ $k$-ti stupac matrice $B.$ Iz uvjeta za postojanje produkta matrica slijedi da ti vektori imaju jednak broj elemenata, tj. oni pripadaju istom vektorskom prostoru, pa se mogu skalarno množiti. Prema definiciji umnoška matrica možemo pisati

$$A\,B=\left[\boldsymbol{a}_{i\cdot}^T\cdot\boldsymbol{b}_{\cdot k}\right].$$