




Next: Linearna nezavisnost.
Up: Operacije s matricama
Previous: Množenje matrica.
Sadržaj
Indeks
Neka je dana matrica 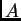 tipa
tipa 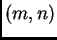
Matrica, koja se iz 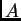 dobije kad reci postanu stupci,
označava se sa
dobije kad reci postanu stupci,
označava se sa 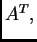 ona je tipa
ona je tipa 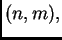 i zove se
transponirana matrica matrice
i zove se
transponirana matrica matrice 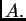 Dakle,
Transponiranje se prema operacijama s matricama odnosi kako slijedi.
Dakle,
Transponiranje se prema operacijama s matricama odnosi kako slijedi.
-
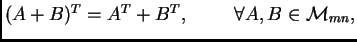
-
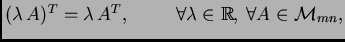
-
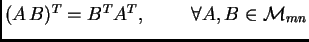
-

2001-10-26
![]() tipa
tipa ![]()
![\begin{displaymath}
% latex2html id marker 30157
A=[a_{ij}]=\left[
\begin{array...
... \\
a_{m1} & a_{m2} & \cdots & a_{mn}
\end{array}
\right].\end{displaymath}](img83.png)
![\begin{displaymath}
% latex2html id marker 30167
A^T=[a_{ij}]^T=[a_{ji}]=\left[ ...
...\
a_{1n} & a_{2n} & \cdots & a_{mn}
\end{array}
\right].
\end{displaymath}](img87.png)