




Next: Kvadratne matrice
Up: Operacije s matricama
Previous: Transponiranje.
Sadržaj
Indeks
Operacije, koje su dane u
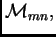 omogućavaju da pravimo linearne
kombinacije matrica. Neka su dane matrice
omogućavaju da pravimo linearne
kombinacije matrica. Neka su dane matrice
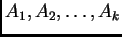 istog
tipa, i brojevi
istog
tipa, i brojevi
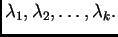 Linearnom kombinacijom matrica
Linearnom kombinacijom matrica
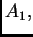
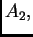
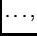
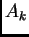 zovemo matricu
zovemo matricu
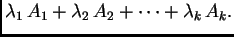 |
(1.2) |
Brojeve
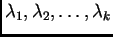 zovemo
koeficijentima linearne kombinacije
(1.2).
zovemo
koeficijentima linearne kombinacije
(1.2).
Definicija 2
Za matrice
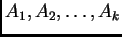
kažemo da su
linearno nezavisne, ako
U protivnom kažemo da su
linearno zavisne.
2001-10-26
![]() omogućavaju da pravimo linearne
kombinacije matrica. Neka su dane matrice
omogućavaju da pravimo linearne
kombinacije matrica. Neka su dane matrice
![]() istog
tipa, i brojevi
istog
tipa, i brojevi
![]() Linearnom kombinacijom matrica
Linearnom kombinacijom matrica
![]()
![]()
![]()
![]() zovemo matricu
zovemo matricu