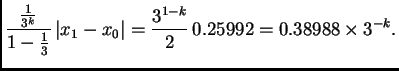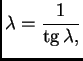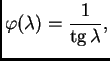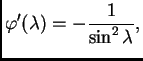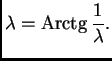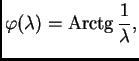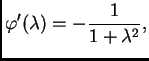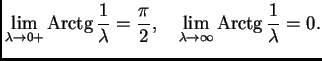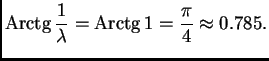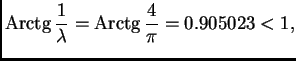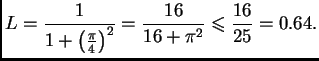Next: Newtonova metoda
Up: Rješavanje jednadžbi
Previous: Metoda polovljenja
Sadržaj
Indeks
Metoda iteracije
Napišimo jednadžbu (3.1) u obliku
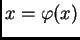 |
(3.4) |
Riješiti jednadžbu sada znači naći takav
![$ s \in [a,b]$](img2428.png) da vrijedi
da vrijedi
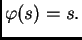 Geometrijski to znači da tražimo presjek grafa
funkcije
Geometrijski to znači da tražimo presjek grafa
funkcije 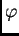 i pravca
i pravca 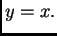
Imamo sljedeći algoritam
Algoritam 2
(Metoda iteracije)
Izaberemo
![$ x_0 \in [a,b],$](img2431.png)
i računamo niz
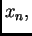
za
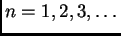
po formuli
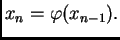 |
(3.5) |
Ako je
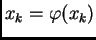
za neki
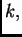
onda je
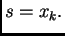
U protivnom
nastavljamo računanje daljnih članova niza.
Imamo sljedeći program za metodu iteracije
Mathematica program 2
(Metoda iteracije)
varphi[t_]=; (* funkcija *)
x=; (* pocetna aproksimacija *)
n=0;
While[
N[f[x]]!=x,
x=varphi[x];
n=n+1;
If[n>100,Break[]]; (* prekid procesa nakon 100 iteracija *)
Print[N[x]]
]
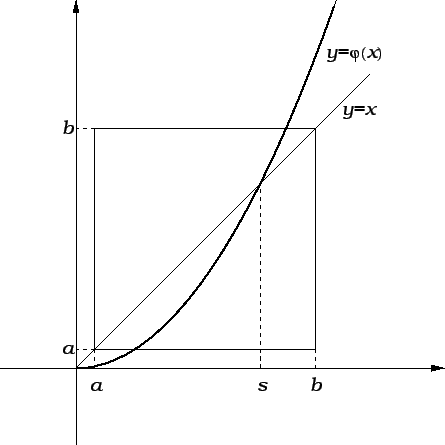
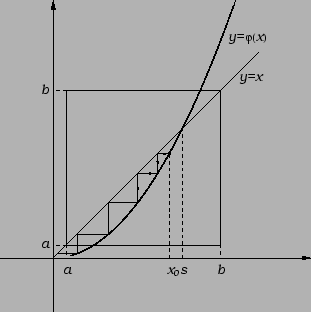
Ovaj algoritam dobro opisuje sljedeća slika.
Može se dogoditi da niz aproksimacija dobiven ovim postupkom ne
konvergira k rješenju, kao na sljedećoj slici.
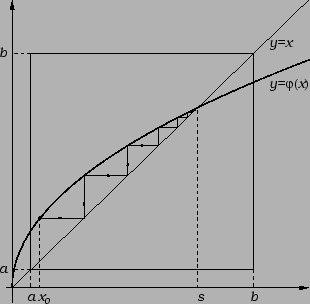
Niz može konvergirati k rješenju, kao na sljedećoj slici.
Evo još nekoliko slika, koje pokazuju različito ponašanje
iteracijskog niza.
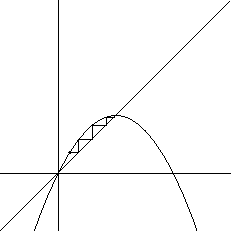
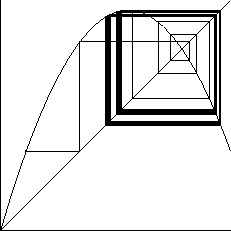
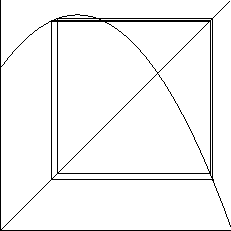
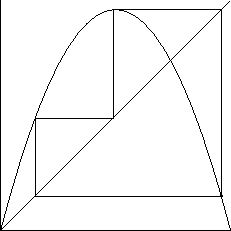

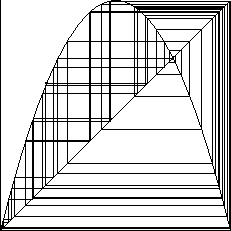
Iz ovih slika, i do sada rečenog, jasno je da moraju biti ispunjeni
neki dodatni uvjeti da bi se dogodilo da iteracijski niz konvergira k
rješenju. Sljedeći teorem daje takve uvjete.
Apriornu ocjenu greške dobivamo na sljedeći način. Iz
slijedi
Za proizvoljni prirodni broj 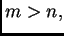 imamo
Ako gornju nejednakost primijenimo na svaki od
članova na desnoj strani, slijedi
Zbog
imamo
Ako gornju nejednakost primijenimo na svaki od
članova na desnoj strani, slijedi
Zbog
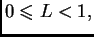 po formuli za sumu geometrijskog reda. Tako je
Desna strana ove nejednakosti ne ovisi o
po formuli za sumu geometrijskog reda. Tako je
Desna strana ove nejednakosti ne ovisi o 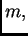 pa prema tome
Dakle apriorna ocjena greške
pa prema tome
Dakle apriorna ocjena greške 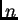 -te aproksimacije je
-te aproksimacije je
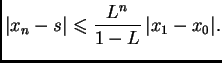 |
(3.6) |
Aposteriorna ocjena greške je ocjena koja se računa pomoću
dobivenih aproksimacija. U ovom slučaju ona je
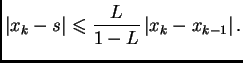 |
(3.7) |
Doista,
Tako je
Primjer 3.3
Riješiti metodom iteracije jednadžbu u primjeru
3.1.
Rješenje. Jednadžbu
možemo prepisati u obliku
Tako je
Rješenje postoji na segmentu
![$ [-2,-1]$](img2371.png)
(v. primjer
3.1).
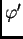
je pozitivna, pa funkcija
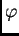
raste. Njezine vrijednosti na rubovima su
Kako
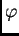
raste,
![$ \varphi(x) \in [-2,-1]$](img2494.png)
za svaki
![$ x \in [-2,-1].$](img2495.png)
Osim toga
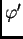
raste na
![$ [-2,-1],$](img2496.png)
pozitivna je, pa najveću
vrijednost ima u
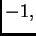
i to
Ova
diskusija pokazuje da su uvjeti teorema
23 ispunjeni, pa
će iteracijski proces konvergirati bez obzira na to koji broj iz
![$ [-2,-1]$](img2371.png)
uzmemo kao početnu aproksimaciju. Ujedno nam ocjena
može poslužiti da bismo
apriorno ocijenili grešku
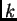
-te aproksimacije.
Imamo na pr.
pa greška
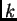
-te aproksimacije nije veća od
Ako želimo rješenje točno na pet decimala, izlazi da mora biti
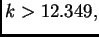
dakle trinaesta aproksimacija daje traženu
točnost. Pomoću programa
2 nalazimo da je
Primjer 3.4
Riješiti zadatak u primjeru
3.2 metodom iteracije.
Rješenje. Jednadžbu treba napisati u obliku
Ako stavimo
onda je
pa je
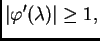
za svaki
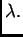
To ne
odgovara uvjetima teorema
23. Jednadžbu možemo i
drukčije napisati
Tada je
pa je
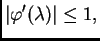
za svaki
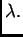
Specijalno,
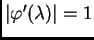
samo za
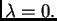
Domena od
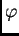
je
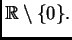
Budući da je
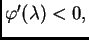
funkcija pada na svakom od intervala
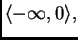
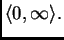
Nas interesiraju samo pozitivna
rješenja, pa nam je interesantan samo interval
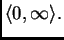
Na tom intervalu
Dakle
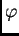
preslikava
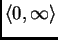
na
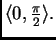
Također, ako je
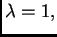
onda je
Zatim, ako uzmemo
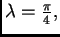
onda je
pa
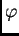
preslikava segment
![$ [\frac{\pi}{4},1]$](img2524.png)
u samog
sebe. Apsolutna vrijednost derivacije je najveća na lijevom
rubu, jer je tada nazivnik najmanji. Tako možemo staviti
To znači da će metoda iteracije konvergirati uzmemo li bilo koji
broj iz segmenta
![$ [\frac{\pi}{4},1]$](img2524.png)
kao
početnu aproksimaciju. Pomoću programa
2 nalazimo da
je zaokruženo na šest decimala, uz
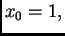
i dalje se ovaj broj ponavlja.
3.1





Next: Newtonova metoda
Up: Rješavanje jednadžbi
Previous: Metoda polovljenja
Sadržaj
Indeks
2001-10-26






![]() niz
niz ![]() definiran algoritmom (3.5) konvergira k jedinstvenom
rješenju jednadžbe
definiran algoritmom (3.5) konvergira k jedinstvenom
rješenju jednadžbe
![]()
![]() Prema uvjetima
teorema,
Prema uvjetima
teorema,
![]() i
i
![]() Budući da je
Budući da je ![]() neprekidna funkcija na segmentu
neprekidna funkcija na segmentu ![]() slijedi da postoji bar jedan
slijedi da postoji bar jedan
![]() takav da je
takav da je ![]() tj.
tj.
![]() dakle
dakle ![]() je
rješenje.
je
rješenje.
![]() i
i ![]() dva međusobno različita
rješenja. Tada, prema Lagrangeovom teoremu srednje vrijednosti,
postoji
dva međusobno različita
rješenja. Tada, prema Lagrangeovom teoremu srednje vrijednosti,
postoji ![]() između
između ![]() i
i ![]() takav da vrijedi
takav da vrijedi
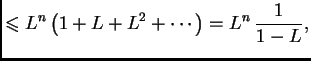
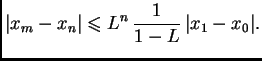
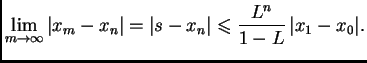
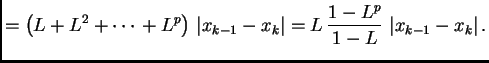
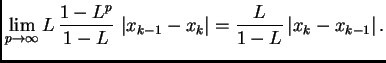
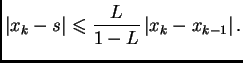
![$\displaystyle \varphi(x) = \sqrt[3]{x-1},\qquad \varphi'(x) = {\frac{1}{3\,{{\left(
x-1 \right) }^{{\frac{2}{3}}}}}}$](img2491.png)
![$\displaystyle \varphi'(-1) = \frac{1}{3\,\sqrt[3]{4}} < \frac{1}{3}.$](img2497.png)
![$\displaystyle L=\max_{x \in [-2,-1]}\vert\varphi'(x)\vert\leqslant{}\varphi'(-1)
\leqslant{}\frac{1}{3}$](img2498.png)