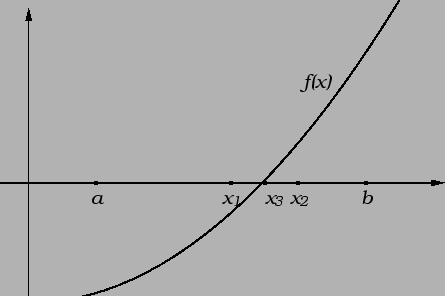

Metoda polovljenja se sastoji u
tome da se segment ![]() na kojem je ispunjen uvjet
na kojem je ispunjen uvjet
![]() raspolovi, tj. nađe polovište
raspolovi, tj. nađe polovište
![]() Ako je
Ako je ![]() onda je
onda je ![]() U protivnom se ponovi operacija na onom od segmenata
U protivnom se ponovi operacija na onom od segmenata
![]() ili
ili ![]() na kojem je ispunjen uvjet (3.2),
itd. Tako imamo sljedeći algoritam.
na kojem je ispunjen uvjet (3.2),
itd. Tako imamo sljedeći algoritam.
Ovaj algoritam omogućava sljedeći program u programskom paketu Mathematica.
f[t_]=; (* funkcija *)
a=;
b=; (* pocetni interval *)
x=(a+b)/2.;
n=0;
Print[{n,a,x,b}];
While[
N[f[x]]!=0.,
If[
f[b]f[x]<0,
a=x;x=(x+b)/2,
b=x;x=(a+x)/2
];
n=n+1;
If[n>100,Break[] (* prekid petlje nakon 100 koraka *)
];
Print[{n,a,x,b}]]
Metoda uvijek konvergira, ali vrlo sporo.
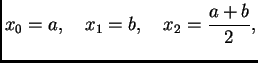
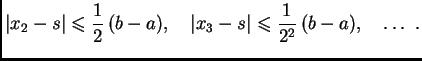
Rješenje. Računanjem vrijednosti polinoma
![]() na skupu
cijelih brojeva, dobivamo da je
na skupu
cijelih brojeva, dobivamo da je ![]() a
a ![]() Tako na
segmentu
Tako na
segmentu ![]() postoji bar jedno rješenje. Ako na ovaj problem
primijenimo gornji program, dobivamo sljedeću tablicu.
postoji bar jedno rješenje. Ako na ovaj problem
primijenimo gornji program, dobivamo sljedeću tablicu.
| 0 | |||
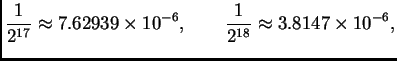
Zadatak iz primjera 3.1 se može doduše egzaktno riješiti pomoću Cardanovih formula. Ipak te formule nisu tako jednostavne kao formula za rješenje kvadratne jednadžbe, pa se algebarske jednadžbe trećeg stupnja često rješavaju približnim metodama. U sljedećem primjeru se rješava jednadžba koju ne možemo egzaktno riješiti.
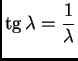
Rješenje. Iz slike 2.7 se vidi da se traženo rješenje nalazi
u intervalu
![]() Neka je
Neka je
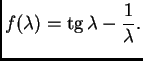
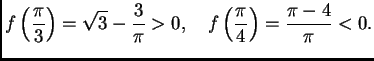
Izračunajmo sada koju aproksimaciju treba naći da bi se
dobila točnost na četiri decimale. Iz formule (3.3)
slijedi da treba naći ![]() tako da bude
tako da bude
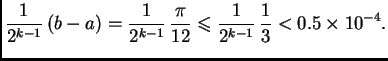
|
|
|
|
|
| 0 | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|