




Next: Metoda polovljenja
Up: Rješavanje jednadžbi
Previous: Rješavanje jednadžbi
Sadržaj
Indeks
Neka je 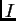 interval u
interval u
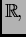
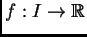 neprekidna
funkcija na
neprekidna
funkcija na 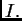 Treba riješiti jednadžbu
Treba riješiti jednadžbu
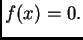 |
(3.1) |
Razmotrit ćemo nekoliko iterativnih postupaka za
rješavanje jednadžbe (3.1), i to metodu
polovljenja, metodu iteracije, Newtonovu metodu i metodu
sekante.
Pretpostavimo da
su 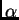 i
i 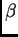 u domeni funkcije
u domeni funkcije 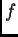 takvi da je
takvi da je
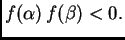 |
(3.2) |
Zbog neprekidnosti funkcije, prema Bolzanovom teoremu (neprekidnost
funkcije na segmentu, v. [10, Teorem 4, str. 31]), postoji barem jedno rješenje 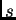 jednadžbe
(3.1) u segmentu
jednadžbe
(3.1) u segmentu
![$ [\alpha{},\beta{}].$](img2344.png)
Iterativni postupak je postupak, kojim nalazimo niz
brojeva
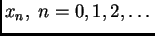 koji predstavljaju približne
vrijednosti rješenja. Cilj je dobiti približno rješenje u granicama
unaprijed dane točnosti. Da bi se to ostvarilo trebaju približna
rješenja
koji predstavljaju približne
vrijednosti rješenja. Cilj je dobiti približno rješenje u granicama
unaprijed dane točnosti. Da bi se to ostvarilo trebaju približna
rješenja 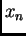 težiti k rješenju
težiti k rješenju 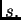 Ako se to događa, tj. ako
niz
Ako se to događa, tj. ako
niz 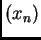 konvergira, i ako je
konvergira, i ako je
onda kažemo da
iterativni postupak konvergira k rješenju. Član 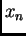 se zove
se zove 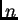 -ta aproksimacija rješenja
-ta aproksimacija rješenja 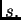 Naravno,
možemo naći samo konačno mnogo članova niza. Tako se moramo
zadovoljiti s približnim rješenjem. Koja će aproksimacija biti
dovoljno dobra ovisi o tome kolika je greška dozvoljiva. Prema tome
bit će nam važno znati ocijeniti grešku koju činimo kad pravo
rješenje
Naravno,
možemo naći samo konačno mnogo članova niza. Tako se moramo
zadovoljiti s približnim rješenjem. Koja će aproksimacija biti
dovoljno dobra ovisi o tome kolika je greška dozvoljiva. Prema tome
bit će nam važno znati ocijeniti grešku koju činimo kad pravo
rješenje 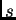 zamjenimo s
zamjenimo s 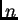 -tom aproksimacijom
-tom aproksimacijom 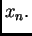





Next: Metoda polovljenja
Up: Rješavanje jednadžbi
Previous: Rješavanje jednadžbi
Sadržaj
Indeks
2001-10-26
![]() interval u
interval u
![]()
![]() neprekidna
funkcija na
neprekidna
funkcija na ![]() Treba riješiti jednadžbu
Treba riješiti jednadžbu
![]() i
i ![]() u domeni funkcije
u domeni funkcije ![]() takvi da je
takvi da je
![]() koji predstavljaju približne
vrijednosti rješenja. Cilj je dobiti približno rješenje u granicama
unaprijed dane točnosti. Da bi se to ostvarilo trebaju približna
rješenja
koji predstavljaju približne
vrijednosti rješenja. Cilj je dobiti približno rješenje u granicama
unaprijed dane točnosti. Da bi se to ostvarilo trebaju približna
rješenja ![]() težiti k rješenju
težiti k rješenju ![]() Ako se to događa, tj. ako
niz
Ako se to događa, tj. ako
niz ![]() konvergira, i ako je
konvergira, i ako je