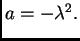... $a = -\lambda^2.$^2.1

Zašto se isključuje $a=0$?

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

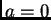...brahistohrona.^2.2

Problem je postavio J. Bernoulli 1696., a riješio ga je iste godine I. Newton.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... drukčije.^2.3

Iz formule koja slijedi može se kao i u slučaju oscilacija napete žice izvesti opća jednadžba gibanja u diferencijalnom obliku. Za to je potrebno dublje poynavanje prirode kontaktne sile i dodatni matematički aparat (v. [21, teorem str. 101]).

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...$(x,y,z).$^2.4

Analogno razmatranje se može provesti, uz očite promjene tehničkog karaktera, i ako je 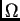$\Omega{}$ područje u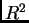 $\\ R^2$

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... ponavlja.^3.1

Uzmemo li u obzir da je 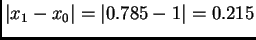$\vert x_1-x_0\vert=\vert.785-1\vert=0.215$ i da je 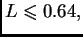$L\leqslant 0.64,$ račun pokazuje da je u dvadesetčetvrtoj aproksimaciji dobivena točnost na pet decimala.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... su^3.2

Vlastite vrijednosti su u ovom i prethodnim primjerima dobivene naredbom Eigenvalue u programskom paketu Mathematica

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.