




Next: Aproksimacija funkcije i numerička
Up: Rješavanje sustava jednadžbi
Previous: Gauss-Seidelova OR-metoda (SOR metoda)
Sadržaj
Indeks
Konvergencija iterativne metode
Iterativni postupci, koje smo upravo definirali, opisani su formulom
gdje je 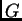 matrica tipa
matrica tipa 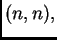 definirana od slučaja do slučaja
na različite načine pomoću matrice
definirana od slučaja do slučaja
na različite načine pomoću matrice 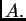 Razmotrimo sada probleme
konvergencije navedenih metoda.
Razmotrimo sada probleme
konvergencije navedenih metoda.
Definicija 16
Neka je
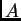
simetrična matrica. Kažemo da je
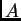 pozitivno definitna
pozitivno definitna, ako vrijedi
Lema 3
Neka je
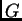
simetrična pozitivno definitna matrica tipa
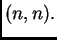
Tada su vlastite vrijednosti
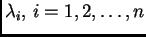
od
matrice
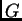
pozitivne, i vrijedi
za svaki
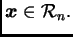
Dokaz. Budući da je matrica 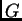 simetrična, postoji
simetrična, postoji 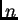 međusobno okomitih i jediničnih vektora
međusobno okomitih i jediničnih vektora
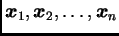 u
u
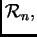 i brojevi
i brojevi
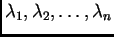 takvih, da je
takvih, da je
Zbog pozitivne definitnosti
Dokažimo sada drugu tvrdnju. Primijetimo
najprije da vlastiti vektori
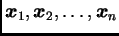 matrice
matrice
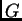 čine ortonormiranu bazu u
čine ortonormiranu bazu u
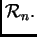 To znači da se bilo koji vektor
To znači da se bilo koji vektor
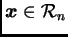 može prikazati kao njihova linearna
kombinacija.
Zbog linearnosti djelovanja matrice
može prikazati kao njihova linearna
kombinacija.
Zbog linearnosti djelovanja matrice 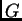 na vektore
Tako je
Odatle
na vektore
Tako je
Odatle
Teorem 25
Neka je
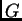
simetrična, pozitivno definitna matrica, i neka su
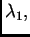
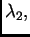
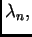
njezine vlastite
vrijednosti. Iterativni postupak
konvergira za bilo koju početnu aproksimaciju
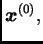
ako i samo ako je
Dokaz. 1. Dokažimo najprije da iz
slijedi konvergencija iterativnog postupka. Doista
i odatle
Odatle možemo, na isti način kao kod računanja apriorne ocjene
greške kod metode iteracije (v. 3.2.2), zaključiti
Budući da je 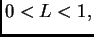 pa niz
pa niz
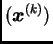 konvergira. Neka je
Tada je
i prema tome niz konvergira k rješenju
konvergira. Neka je
Tada je
i prema tome niz konvergira k rješenju
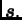
2. Dokažimo obrat, tj. da iz konvergencije postupka slijedi
Iz
i
slijedi
Zbog pretpostavke
slijedi
Ako se to događa za svaku početnu aproksimaciju
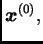 onda mora biti
Budući da je
onda mora biti
Budući da je 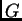 simetrična matrica, ona se može dijagonalizirati,
tj. postoji regularna matrica
simetrična matrica, ona se može dijagonalizirati,
tj. postoji regularna matrica 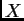 takva, da vrijedi
takva, da vrijedi
![% latex2html id marker 39177
$\displaystyle G^k = X\,\left[\begin{array}{cccc}
...
... \ddots & \vdots \\
0 & 0 & \cdots & \lambda_n^k
\end{array}\right]\,X^{-1},$](img2857.png)
za
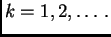
Odatle
Ako pomnožimo s lijeva s 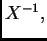 i s desna s
i s desna s 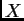 , slijedi
Prema tome
Zbog
, slijedi
Prema tome
Zbog
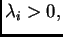 to je moguće samo ako je
to je moguće samo ako je
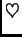
Na isti način kao kod metode iteracije prilikom traženja
nultočke funkcije možemo naći apriornu ocjenu greške
i aposteriornu ocjenu greške
Ovi rezultati su dobiveni uz pretpostavku da je 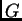 simetrična
pozitivno definitna matrica. To je važan slučaj, koji se pojavljuje
prilikom približnog rješavanja rubnih i rubno-početnih problema
varijacijskim metodama. Međutim, može se dogoditi da
simetrična
pozitivno definitna matrica. To je važan slučaj, koji se pojavljuje
prilikom približnog rješavanja rubnih i rubno-početnih problema
varijacijskim metodama. Međutim, može se dogoditi da 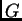 ne
ispunjava ovaj uvjet. Ipak, dobiveni rezultati vrijede i tada uz neke
modifikacije.
ne
ispunjava ovaj uvjet. Ipak, dobiveni rezultati vrijede i tada uz neke
modifikacije.
Prije svega, budući da u općem slučaju vlastite vrijednosti mogu
biti kompleksni brojevi, broj
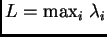 više nema
smisla, jer u skupu kompleksnih brojeva nemamo prirodni
uređaj. Umjesto toga imamo ovu definiciju.
više nema
smisla, jer u skupu kompleksnih brojeva nemamo prirodni
uređaj. Umjesto toga imamo ovu definiciju.
Definicija 17
Neka je
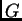
matrica tipa
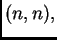
i neka su
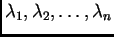
njezine vlastite
vrijednosti. Broj
se zove
spektralni radius matrice
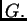
Očito je u slučaju simetričnosti i pozitivne definitnosti matrice
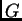
Može se dokazati sljedeći teorem
Teorem 26
Iterativni postupak
konvergira za bilo koju početnu aproksimaciju
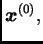
ako i samo ako je
Tako se problem konvergencije iterativnog postupka svodi na problem
ocjene spektralnog radiusa, odnosno najveće po modulu (apsolutnoj
vrijednosti) vlastite vrijednosti matrice, i to ocjene odozgo. Ima
raznih ocjena te vrste. Navedimo neke od njih. Neka je
![$ G=[g_{i\,j}].$](img2872.png) Tada vrijedi
Tada vrijedi
-
![$ \nu(G)\leqslant
\left[\sum_{i=1}^n\sum_{j=1}^n\vert g_{ij}\vert^2\right]^{\frac{1}{2}},$](img2873.png)
-
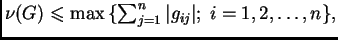
-
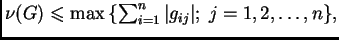
Ako je bilo koji od ovih brojeva na desnoj strani manji od 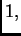 spektralni radius je nužno manji od
spektralni radius je nužno manji od 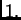 Naglasimo da se ovdje ne
radi o spektralnom radiusu matrice
Naglasimo da se ovdje ne
radi o spektralnom radiusu matrice 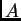 već matrice
već matrice 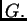
Primjer 3.12
Ispitati konvergenciju Jacobijeve i Gauss-Seidelove metode u
primjeru
3.10.
Rješenje. Kod Jacobijeve metode imamo
a kod Gauss-Seidelove
Matrica sustava, kako je na početku napisan, je
Ako primijenimo Jacobijevu metodu, imamo
Vlastite vrijednosti su
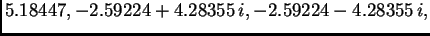
pa je spektralni radius
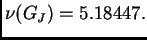
Kod Gauss-Seidelove metode imamo još lošiji rezultat
Vlastite vrijednosti su
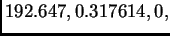
pa je spektralni radius
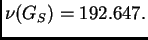
Kad prvu jednadžbu stavimo na treće mjesto, Jacobijeva metoda daje
zatim vlastite vrijednosti su
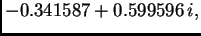
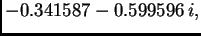
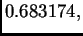
pa je spektralni radius
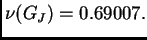
zatim vlastite vrijednosti su
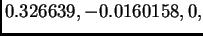
pa
je spektralni radius
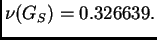
Ako se radi Gauss-Seidelovom
OR metodom, spektralni radius postaje
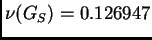
za
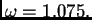
Primjer 3.13
Neka je matrica sustava
Treba ispitati da li Jacobijev i Gauss-Seidelov postupak konvergiraju.
Rješenje. U Jacobijevom postupku je
Njezine vlastite vrijednosti su
spektralni radius je
i prema tome Jacobijeva metoda konvergira za svaku početnu
aproksimaciju.
Kod Gauss-Seidelove metode je
Njezine vlastite vrijednosti
su
3.2
spektralni radius je sada
pa prema tome Gauss-Seidelova metoda također konvergira za svaku
početnu aproksimaciju, i to brže nego Jacobijeva.
S porastom reda matrice, uz isti tridijagonalni oblik, vlastite
vrijednosti matrice 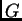 rastu prema
rastu prema 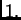 U slučajevima kad su vrlo
blizu broju
U slučajevima kad su vrlo
blizu broju 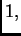 OR metode postaju vrlo efikasne u smislu brzine
konvergencije.
OR metode postaju vrlo efikasne u smislu brzine
konvergencije.





Next: Aproksimacija funkcije i numerička
Up: Rješavanje sustava jednadžbi
Previous: Gauss-Seidelova OR-metoda (SOR metoda)
Sadržaj
Indeks
2001-10-26
![]() simetrična, postoji
simetrična, postoji ![]() međusobno okomitih i jediničnih vektora
međusobno okomitih i jediničnih vektora
![]() u
u
![]() i brojevi
i brojevi
![]() takvih, da je
takvih, da je
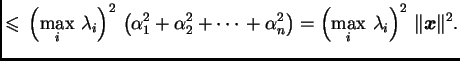
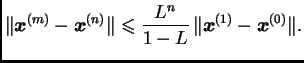
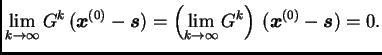
![% latex2html id marker 39177
$\displaystyle G^k = X\,\left[\begin{array}{cccc}
...
... \ddots & \vdots \\
0 & 0 & \cdots & \lambda_n^k
\end{array}\right]\,X^{-1},$](img2857.png) za
za ![% latex2html id marker 39180
$\displaystyle \lim_{k\rightarrow{}\infty{}} G^k= \...
...\ddots & \vdots \\
0 & 0 & \cdots & \lambda_n^k
\end{array}\right]\,X^{-1} =$](img2858.png)
![% latex2html id marker 39182
$\displaystyle = X\,\left(\lim_{k\rightarrow{}\inft...
... \vdots \\
0 & 0 & \cdots & \lambda_n^k
\end{array}\right]\right)\,X^{-1} = $](img2859.png)
![% latex2html id marker 39184
$\displaystyle = X\,
\left[\begin{array}{cccc}
\l...
...ots & \lim_{k\rightarrow{}\infty{}}\lambda_n^k
\end{array}\right]\,X^{-1} = O.$](img2860.png)
![% latex2html id marker 39190
$\displaystyle \left[\begin{array}{cccc}
\lim_{k\r...
... 0 & \cdots & \lim_{k\rightarrow{}\infty{}}\lambda_n^k
\end{array}\right] = O.$](img2861.png)
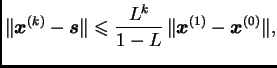
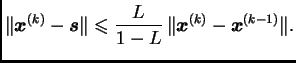
![]() simetrična
pozitivno definitna matrica. To je važan slučaj, koji se pojavljuje
prilikom približnog rješavanja rubnih i rubno-početnih problema
varijacijskim metodama. Međutim, može se dogoditi da
simetrična
pozitivno definitna matrica. To je važan slučaj, koji se pojavljuje
prilikom približnog rješavanja rubnih i rubno-početnih problema
varijacijskim metodama. Međutim, može se dogoditi da ![]() ne
ispunjava ovaj uvjet. Ipak, dobiveni rezultati vrijede i tada uz neke
modifikacije.
ne
ispunjava ovaj uvjet. Ipak, dobiveni rezultati vrijede i tada uz neke
modifikacije.
![]() više nema
smisla, jer u skupu kompleksnih brojeva nemamo prirodni
uređaj. Umjesto toga imamo ovu definiciju.
više nema
smisla, jer u skupu kompleksnih brojeva nemamo prirodni
uređaj. Umjesto toga imamo ovu definiciju.
![]()
![]() Tada vrijedi
Tada vrijedi
![]() spektralni radius je nužno manji od
spektralni radius je nužno manji od ![]() Naglasimo da se ovdje ne
radi o spektralnom radiusu matrice
Naglasimo da se ovdje ne
radi o spektralnom radiusu matrice ![]() već matrice
već matrice ![]()
![% latex2html id marker 39253
$\displaystyle A = \left[
\begin{array}{rrr}
1.00...
...3.72 \\
3.15 & - 0.20 & - 1.97 \\
4.43 & 5.84 & 1.79
\end{array}
\right].$](img2878.png)
![% latex2html id marker 39255
$\displaystyle G_J = \left[\begin{array}{rrr}
0 & ...
... -3.72 \\
15.75 & 0 & -9.85 \\
-2.47486 & -3.26257 & 0
\end{array}\right].$](img2879.png)
![% latex2html id marker 39261
$\displaystyle G_S = \left[\begin{array}{rrr}
0 & ...
...3.72 \\
0 & -39.5325 & -68.44 \\
0 & 135.189 & 232.497
\end{array}\right].$](img2882.png)
![% latex2html id marker 39267
$\displaystyle G_J = \left[
\begin{array}{rrr}
0 ...
...-0.758562 & 0 & -0.306507 \\
-0.268817 & -0.674731 & 0
\end{array}
\right],$](img2885.png)
![% latex2html id marker 39277
$\displaystyle G_S = \left[ \begin{array}{rrr} 0 & ...
...\\ 0 &
-0.0481626 & -0.780909 \\ 0 & 0.0154291 & 0.358786 \end{array}\right],$](img2890.png)
![% latex2html id marker 39288
$\displaystyle A = \left[
\begin{array}{rrrr}
2 &...
... 2 & -1 & 0 \\
0 & -1 & 2 & -1 \\
0 & 0 & -1 & 2 \\
\end{array}
\right].$](img2895.png)
![% latex2html id marker 39290
$\displaystyle G = - D^{-1}(L+R) = \left[
\begin{a...
... 1/2 & 0 \\
0 & 1/2 & 0 & 1/2 \\
0 & 0 & 1/2 & 0 \\
\end{array}
\right].$](img2896.png)
![% latex2html id marker 39296
$\displaystyle G = -(L + D)^{-1}\,R = \left[ \begin...
... & 0 \\ 0 & 1/8 & 1/4 & 1/2 \\ 0 & 1/16 & 1/8 & 1/4 \\
\end{array} \right].$](img2899.png)
![]() rastu prema
rastu prema ![]() U slučajevima kad su vrlo
blizu broju
U slučajevima kad su vrlo
blizu broju ![]() OR metode postaju vrlo efikasne u smislu brzine
konvergencije.
OR metode postaju vrlo efikasne u smislu brzine
konvergencije.