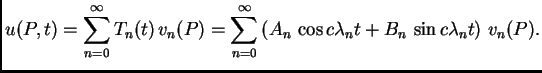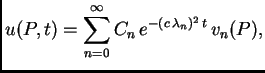Next: Varijacijski princip
Up: Metoda separacije varijabli (Fourierova
Previous: Ravnoteža pravokutne membrane
Sadržaj
Indeks
Metoda separacije varijabli za nestacionarne probleme
Nestacionarni problemi su opisani valnom jednadžbom
ili jednadžbom provođenja
na nekom području
 u
u  Ovdje smo radi jednostavnosti uzeli da su
gustoća mase
Ovdje smo radi jednostavnosti uzeli da su
gustoća mase 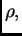 i specifična toplina
i specifična toplina 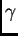 konstante.
Također smo pretpostavili da nema vanjskog utjecaja, tj. da je
konstante.
Također smo pretpostavili da nema vanjskog utjecaja, tj. da je
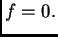
Pretpostavimo da je rubni uvjet Dirichletov
Ovdje je, zbog
kratkoće zapisa, stavljeno 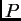 umjesto
umjesto 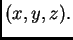 2.4 Početni uvjeti za
valnu jednadžbu neka su
za
2.4 Početni uvjeti za
valnu jednadžbu neka su
za
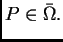 Ovdje
Ovdje
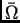 označava područje
označava područje
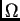 zajedno s rubom
zajedno s rubom
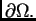
Osnovna pretpostavka je da se rješenje može predstaviti u obliku
produkta
Uvrstimo u jednadžbu, na pr. valnu
i podijelimo s
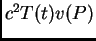 Budući da smo separirali varijable, i da su one nezavisne,
Budući da smo separirali varijable, i da su one nezavisne, 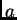 je
konstanta.
Pomnožimo ovu jednadžbu s
je
konstanta.
Pomnožimo ovu jednadžbu s 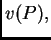 i integriramo po
i integriramo po 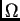 Imamo, zbog
(2.53),
jer se
Imamo, zbog
(2.53),
jer se 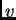 poništava na
poništava na
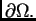 Tako je
Dakle možemo staviti
Tako je
Dakle možemo staviti
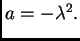 Tako se početna jednadžba
raspada na dvije jednadžbe
Rubni uvjet je sada
Tako se početna jednadžba
raspada na dvije jednadžbe
Rubni uvjet je sada
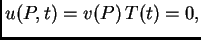
za
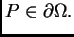
Kako to vrijedi za svaki 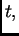 mora biti
mora biti 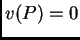 na
na
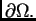 Tako imamo rubni problem
Oni
Tako imamo rubni problem
Oni
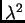 za koje postoji netrivijalno rješenje ovog problema
zovu se vlastite vrijednosti, a pripadne
funkcije
vlastite funkcije ovog rubnog problema.
za koje postoji netrivijalno rješenje ovog problema
zovu se vlastite vrijednosti, a pripadne
funkcije
vlastite funkcije ovog rubnog problema.
Neka su 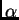 i
i 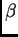 dvije međusobno različite vlastite
vrijednosti, i
dvije međusobno različite vlastite
vrijednosti, i 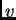 odnosno
odnosno 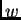 pripadne vlastite funkcije. Tada
pripadne vlastite funkcije. Tada
S druge strane, prema drugoj
Greenovoj formuli, koja se izvodi iz (2.53),
jer je
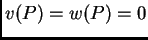 za
za
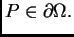 Tako je
Budući da je
Tako je
Budući da je
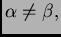 slijedi
Zbog ovog svojstva kažemo da su vlastite funkcije, koje pripadaju
različitim vlastitim vrijednostima, međusobno okomite. Opravdanje
leži u činjenici da produkt
koji paru funkcija pridružuje broj (skalar),
ima sva svojstva skalarnog produkta.
slijedi
Zbog ovog svojstva kažemo da su vlastite funkcije, koje pripadaju
različitim vlastitim vrijednostima, međusobno okomite. Opravdanje
leži u činjenici da produkt
koji paru funkcija pridružuje broj (skalar),
ima sva svojstva skalarnog produkta.
Pretpostavimo sada da su
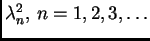 vlastite
vrijednosti, a
vlastite
vrijednosti, a
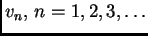 vlastite funkcije rubnog
problema. Tada vremenska jednadžba glasi
vlastite funkcije rubnog
problema. Tada vremenska jednadžba glasi
Rješenja su
Rješenje cijelog rubno-početnog problema tražimo u obliku
Neodređene konstante
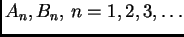 računamo iz
početnih uvjeta, pomoću Fourierovih redova.
računamo iz
početnih uvjeta, pomoću Fourierovih redova.
Kod jednadžbe provođenja jedina je razlika u vremenskoj
jednadžbi. Ona u tom slučaju glasi
pa je
Rješenje cijelog problema se tada traži u obliku
a neodređene konstante 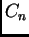 se određuju iz početnog uvjeta pomoću
Fourierovog reda.
se određuju iz početnog uvjeta pomoću
Fourierovog reda.





Next: Varijacijski princip
Up: Metoda separacije varijabli (Fourierova
Previous: Ravnoteža pravokutne membrane
Sadržaj
Indeks
2001-10-26
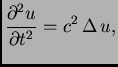
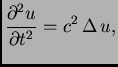
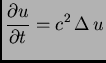
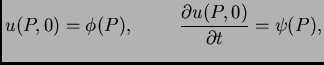
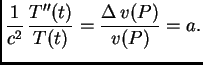
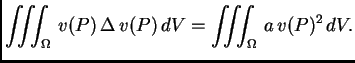
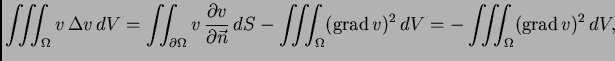
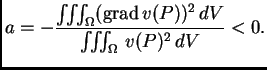
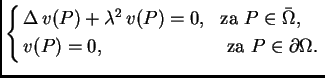
![]() i
i ![]() dvije međusobno različite vlastite
vrijednosti, i
dvije međusobno različite vlastite
vrijednosti, i ![]() odnosno
odnosno ![]() pripadne vlastite funkcije. Tada
pripadne vlastite funkcije. Tada
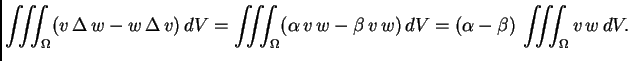
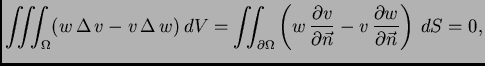
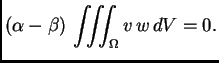
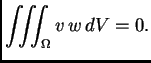
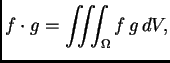
![]() vlastite
vrijednosti, a
vlastite
vrijednosti, a
![]() vlastite funkcije rubnog
problema. Tada vremenska jednadžba glasi
vlastite funkcije rubnog
problema. Tada vremenska jednadžba glasi