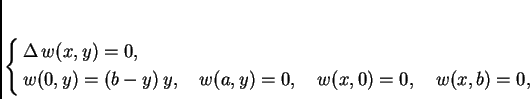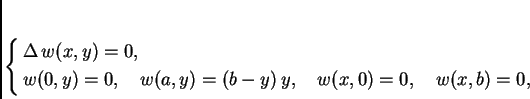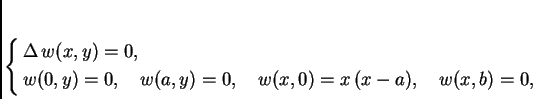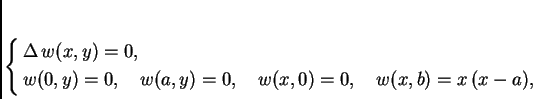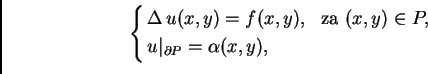
Rubni problem za ravnotežu pravokutne membrane učvršćene na rubu glasi
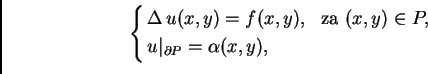
Pretpostavimo da je ![]() i da je
i da je
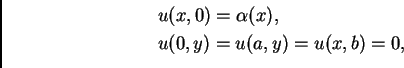
Pretpostavimo rješenje u obliku
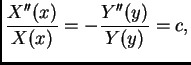
Tako imamo
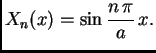
Druga jednadžba
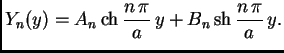
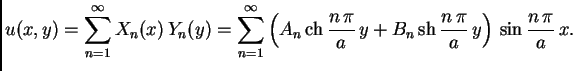
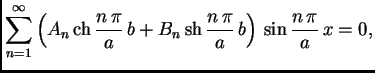
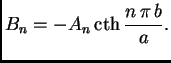
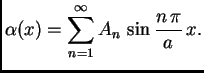
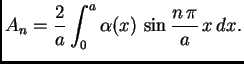
Ako je uvjet na rubu složeniji, onda se problem rastavlja na nekoliko ovakvih.
Rješenje. Treba riješiti problem
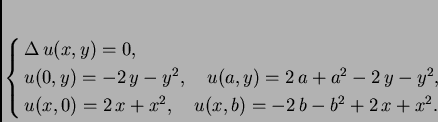
Objasnili smo kako se rješava rubni problem za ravnotežu pravokutne membrane u slučaju kad je rubni uvjet homogen na tri od četiri ruba. Ovaj problem ćemo riješiti tako da ga rastavimo na nekoliko problema, od kojih je svaki problem tipa koji smo objasnili.
Prvi korak je da pogodnom, jednostavnom, supstitucijom osiguramo
da pomak membrane u vrhovima pravokutnika bude ![]() Stavimo
Stavimo
| 0 | |||
| 0 | |||
| 0 | |||
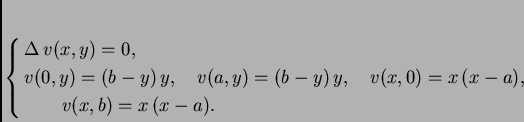
Neka je ![]() rješenje rubnog problema
rješenje rubnog problema