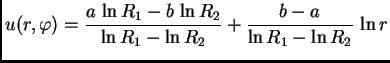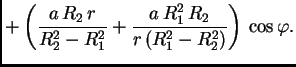U tom slučaju imamo dva rubna uvjeta
![$\displaystyle u(r,\varphi) = C_{0} + D_{0}\,\ln r + \sum_{n=1}^{\infty}
\left[...
...\varphi + \left(C_{2n}\,r^n + \frac{D_{2n}}{r^n}\right)\,\sin
n\varphi\right].$](img2155.png)
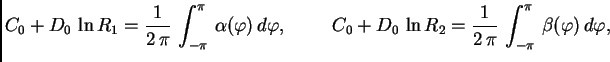
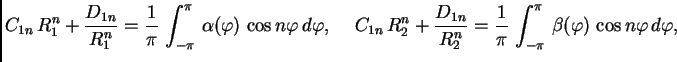
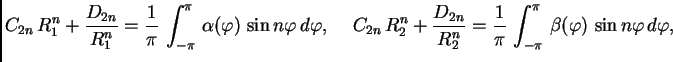
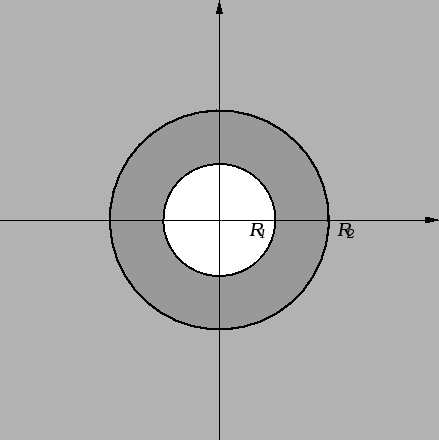
Rješenje. Beskonačnost cijevi nam, zajedno s homogenošću omogućuje da na problem gledamo kao na dvodimenzionalni. U tom slučaju se, naime, u svakom poprečnom presjeku uspostavi isto ravnotežno stanje. Problem je prema tome ekvivalentan problemu toplinske ravnoteže unutar prstena, tj. rubnom problemu
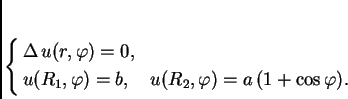
![$\displaystyle u(r,\varphi) = C_{0} + D_{0}\,\ln r + \sum_{n=1}^{\infty}
\left[...
...\varphi + \left(C_{2n}\,r^n + \frac{D_{2n}}{r^n}\right)\,\sin
n\varphi\right],$](img2166.png)
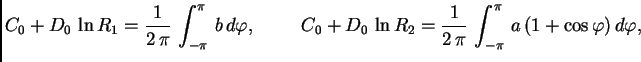
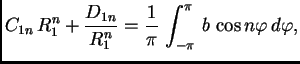
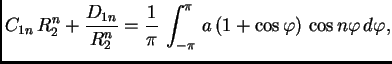
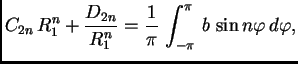
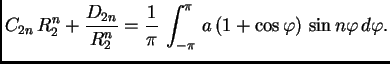
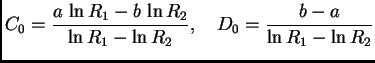
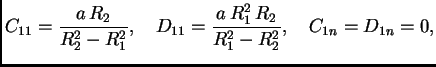 za
za