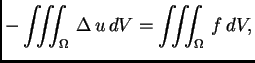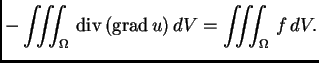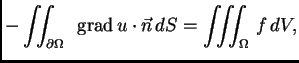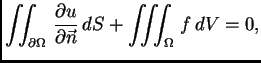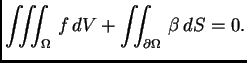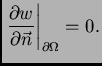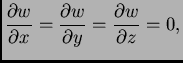Next: Metoda separacije varijabli (Fourierova
Up: Rubni problemi
Previous: Rubni problemi
Sadržaj
Indeks
Jedinstvenost rješenja rubnih problema
Laplaceova jednadžba ima beskonačno mnogo rješenja. Dovoljno je
vidjeti da je funkcije oblika
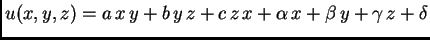 zadovoljavaju, za bilo
kakve vrijednosti parametara
zadovoljavaju, za bilo
kakve vrijednosti parametara
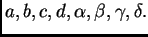 Tako i Poissonova jednadžba ima beskonačno mnogo rješenja. Realna
fizikalna situacija je membrana određenog oblika, s određenim
uvjetima na rubu. To drastično smanjuje broj rješenja. Razmotrimo
sada problem jedinstvenosti rubnog problema
Tako i Poissonova jednadžba ima beskonačno mnogo rješenja. Realna
fizikalna situacija je membrana određenog oblika, s određenim
uvjetima na rubu. To drastično smanjuje broj rješenja. Razmotrimo
sada problem jedinstvenosti rubnog problema
Taj problem ćemo rješavati pomoću energetske jednadžbe. Pomnožimo Poissonovu jednadžbu s  i zatim
integrirajmo po cijelom području
i zatim
integrirajmo po cijelom području
Za skalarna polja  i
i 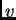 imamo
imamo
Stavimo 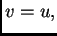 pa imamo
pa imamo
 |
(2.51) |
Po teoremu o divergenciji
pa nakon uvrštavanja dobivamo
energetsku jednadžbu
Teorem 19
Neka je
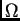
ograničeno područje u
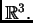
Dirichletov rubni
problem
ima najviše jedno rješenje.
Dokaz. Zaista, pretpostavimo da su
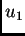 i
i 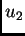 dva rješenja. Tada funkcija
dva rješenja. Tada funkcija
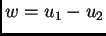 rješava rubni problem
rješava rubni problem
Uvrstimo 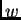 u energetsku jednadžbu umjesto
u energetsku jednadžbu umjesto 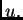 Imamo
Slijedi
odakle
pa je
Imamo
Slijedi
odakle
pa je 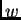 konstanta. No,
konstanta. No,
 povlači
povlači 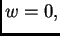 tj.
tj.
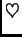
Teorem 20
Neka je
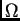
ograničeno područje u
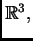
i neka je zadan
Neumannov rubni problem
- Nužan uvjet za postojanje rješenja je
- Bilo koja dva rješenja se razlikuju za konstantu.
Dokaz. 1. Ako je  rješenje, onda
iz jednadžbe slijedi
rješenje, onda
iz jednadžbe slijedi
Po teoremu o divergenciji slijedi
dakle
Ovaj uvjet izražava činjenicu da vanjska sila i Neumannov rubni
uvjet moraju biti pažljivo izabrani, tako da membrana bude u
ravnoteži. Kod Dirichletovog uvjeta nije bio potreban toliki oprez,
jer je u tom slučaju membrana na rubu učvršćena.
2. Neka su 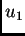 i
i
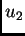 dva rješenja. Tada funkcija
dva rješenja. Tada funkcija
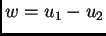 rješava rubni problem
Uvrstimo
rješava rubni problem
Uvrstimo 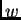 u energetsku jednadžbu umjesto
u energetsku jednadžbu umjesto 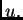 Imamo
Slijedi
odakle
pa je
Imamo
Slijedi
odakle
pa je 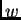 konstanta. Tako
se
konstanta. Tako
se 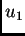 i
i 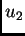 razlikuju za konstantu.
razlikuju za konstantu.





Next: Metoda separacije varijabli (Fourierova
Up: Rubni problemi
Previous: Rubni problemi
Sadržaj
Indeks
2001-10-26
![]() zadovoljavaju, za bilo
kakve vrijednosti parametara
zadovoljavaju, za bilo
kakve vrijednosti parametara
![]() Tako i Poissonova jednadžba ima beskonačno mnogo rješenja. Realna
fizikalna situacija je membrana određenog oblika, s određenim
uvjetima na rubu. To drastično smanjuje broj rješenja. Razmotrimo
sada problem jedinstvenosti rubnog problema
Tako i Poissonova jednadžba ima beskonačno mnogo rješenja. Realna
fizikalna situacija je membrana određenog oblika, s određenim
uvjetima na rubu. To drastično smanjuje broj rješenja. Razmotrimo
sada problem jedinstvenosti rubnog problema
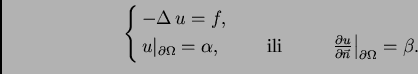
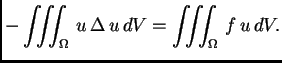
![]() i
i ![]() imamo
imamo
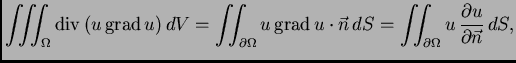
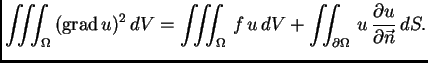
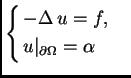
![]() i
i ![]() dva rješenja. Tada funkcija
dva rješenja. Tada funkcija
![]() rješava rubni problem
rješava rubni problem

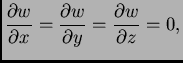
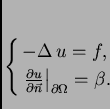
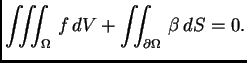
![]() rješenje, onda
iz jednadžbe slijedi
rješenje, onda
iz jednadžbe slijedi