Next: Provođenje topline
Up: Oscilacije membrane
Previous: Oscilacije membrane
Sadržaj
Indeks
Zakon održanja.
Količina gibanja u jedinici vremena komada membrane 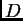 jednaka je ukupnoj količini gibanja koja se po jedinici
vremena izvana prenese na membranu, kroz rub i
drukčije.2.3
jednaka je ukupnoj količini gibanja koja se po jedinici
vremena izvana prenese na membranu, kroz rub i
drukčije.2.3
Promatrat ćemo samo male transverzalne oscilacije, pa je tako
Prvi zakon ponašanja kaže da je gustoća količine gibanja jednaka
umnošku gustoće mase i brzine
Drugi zakon ponašanja se izvodi slično kao kod žice.
Vektorsko polje
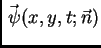 je tangencijalno na
membranu i okomito na luk
je tangencijalno na
membranu i okomito na luk  Uzdužna komponenta kontaktne sile
je, zbog pretpostavke o izotropnoj napetosti, uvijek okomita na
rub, i po iznosu konstantna, pa nas interesira samo
Uzdužna komponenta kontaktne sile
je, zbog pretpostavke o izotropnoj napetosti, uvijek okomita na
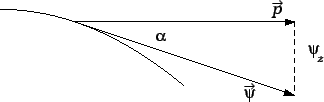
rub, i po iznosu konstantna, pa nas interesira samo 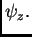 Iz slike
vidimo da je
Iz slike
vidimo da je
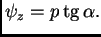 Zatim, iz geometrijske
interpretacije derivacije slijedi
Zatim, iz geometrijske
interpretacije derivacije slijedi
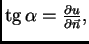 pa je
pa je
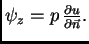 Također ćemo pretpostaviti da vanjska sila
djeluje samo u smjeru okomitom na membranu, pa ćemo tako u daljnjem
promatrati samo
Također ćemo pretpostaviti da vanjska sila
djeluje samo u smjeru okomitom na membranu, pa ćemo tako u daljnjem
promatrati samo
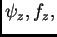 i te veličine ćemo označavati s
i te veličine ćemo označavati s
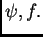 Imamo dakle drugi zakon ponašanja
Uvrstimo zakone ponašanja u zakon održanja i primijenimo Leibnizovo
pravilo o deriviranju pod znakom integrala. Dobivamo
Na prvi integral na desnoj strani primijenimo teorem o divergenciji,
pa imamo
Imamo dakle drugi zakon ponašanja
Uvrstimo zakone ponašanja u zakon održanja i primijenimo Leibnizovo
pravilo o deriviranju pod znakom integrala. Dobivamo
Na prvi integral na desnoj strani primijenimo teorem o divergenciji,
pa imamo
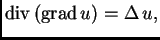 pa kad to uvrstimo, prebacimo sve na lijevu
stranu i stavimo pod jedan integral, dobivamo
Budući da ova jednakost vrijedi za svaki komad membrane
pa kad to uvrstimo, prebacimo sve na lijevu
stranu i stavimo pod jedan integral, dobivamo
Budući da ova jednakost vrijedi za svaki komad membrane  slijedi
tj.
Ova
jednadžba se zove valna jednadžba. Ona opisuje male
poprečne oscilacije izotropno napete membrane.
slijedi
tj.
Ova
jednadžba se zove valna jednadžba. Ona opisuje male
poprečne oscilacije izotropno napete membrane.
U slučaju da 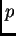 nije konstantno, dobili bismo jednadžbu
nije konstantno, dobili bismo jednadžbu





Next: Provođenje topline
Up: Oscilacije membrane
Previous: Oscilacije membrane
Sadržaj
Indeks
2001-10-26
![]() jednaka je ukupnoj količini gibanja koja se po jedinici
vremena izvana prenese na membranu, kroz rub i
drukčije.2.3
jednaka je ukupnoj količini gibanja koja se po jedinici
vremena izvana prenese na membranu, kroz rub i
drukčije.2.3
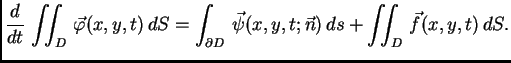
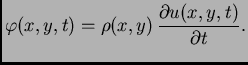

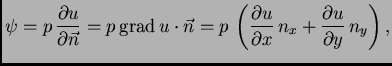
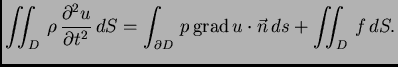
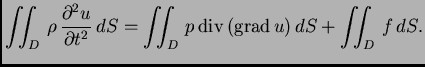
![$\displaystyle \iint_{D}\,\left[\rho\,\frac{\partial^2 u}{\partial t^2} - p\,\Delta\,u -
f\right]\,dS = 0.$](img2025.png)
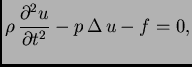
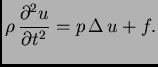
![]() nije konstantno, dobili bismo jednadžbu
nije konstantno, dobili bismo jednadžbu