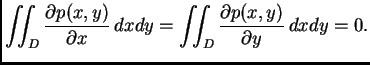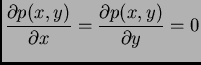Next: Zakon održanja.
Up: Rubni problemi
Previous: Rubni problemi
Sadržaj
Indeks
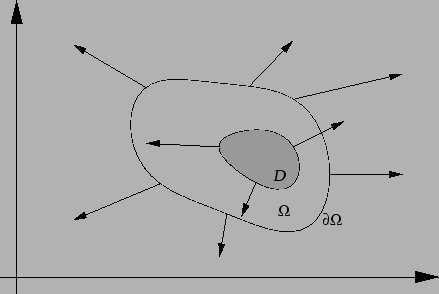
Oscilacije membrane
Membrana je tanka ploča od krutog materijala. Promatrat ćemo
membranu napetu silama koje djeluju u ravnini membrane. Sila djeluje
na luk krivulje koja je rub membrane. Zbog krutosti membrane, napetost
uslijed te sile prenosi se u unutrašnjost, pa tako na svaki komad
membrane  djeluje napetost na rubu
djeluje napetost na rubu
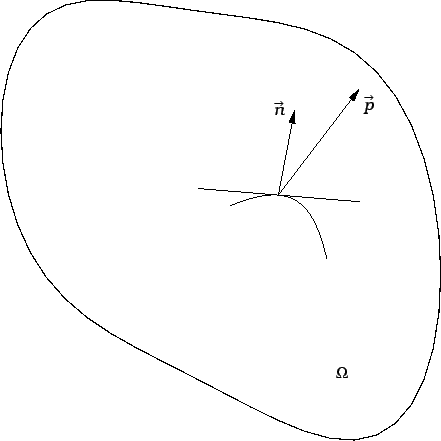
 Tako, u svakoj točki
Tako, u svakoj točki 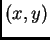 membrane, i za svaki luk kroz točku
membrane, i za svaki luk kroz točku
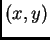 imamo silu
imamo silu 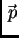 po jedinici duljine luka, kojom jedan
dio membrane djeluje na drugi dio. Njezino djelovanje je omogućeno
isključivo kontaktom, i ona je paralelna s ravninom membrane.
Pretpostavljamo, radi jednostavnosti, da napetost ne ovisi o vremenu.
Osnovna pretpostavka je da je
po jedinici duljine luka, kojom jedan
dio membrane djeluje na drugi dio. Njezino djelovanje je omogućeno
isključivo kontaktom, i ona je paralelna s ravninom membrane.
Pretpostavljamo, radi jednostavnosti, da napetost ne ovisi o vremenu.
Osnovna pretpostavka je da je 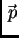 isto za sve lukove kroz
isto za sve lukove kroz
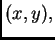 koji imaju zajednički jedinični vektor normale
koji imaju zajednički jedinični vektor normale 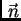 u točki
u točki 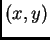 (Cauchyjev aksiom).
Tako
(Cauchyjev aksiom).
Tako
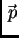 ovisi samo o točki i jediničnom vektoru normale u točki,
tj.
ovisi samo o točki i jediničnom vektoru normale u točki,
tj.
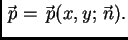 Ta ovisnost je
linearna, pa prema tome, ako je
onda vrijedi
Ta ovisnost je
linearna, pa prema tome, ako je
onda vrijedi
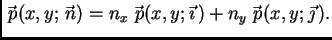 |
(2.42) |
Prema tome napetost 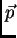 je određena svojim djelovanjem na
vektore
je određena svojim djelovanjem na
vektore
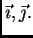 Linearna ovisnost
Linearna ovisnost 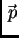 o
vektoru normale omogućava da se napetost shvati kao linearno
preslikavanje (linearni operator) i prema tome opiše matricom. Neka
je
o
vektoru normale omogućava da se napetost shvati kao linearno
preslikavanje (linearni operator) i prema tome opiše matricom. Neka
je
Time je napetost u točki 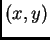 dana matricom
dana matricom
![% latex2html id marker 36209
$\displaystyle {\cal P}(x,y) = \left[ \begin{array}{cc} p_{11}(x,y) & p_{12}(x,y) \\ p_{21}(x,y) & p_{22}(x,y) \end{array}\right].$](img1970.png) |
(2.45) |
Napetost u
smjeru vektora 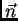 možemo izračunati tako da identificiramo
radijvektore s vektorstupcima, i da zatim vektorstupac
možemo izračunati tako da identificiramo
radijvektore s vektorstupcima, i da zatim vektorstupac
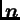 pomnožimo matricom
pomnožimo matricom 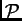 To isto se dobije, ako uvrstimo (2.45) i (2.46) u
(2.44). Tako možemo pisati
To isto se dobije, ako uvrstimo (2.45) i (2.46) u
(2.44). Tako možemo pisati
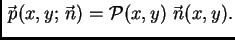 |
(2.46) |
Pretpostavljamo da je membrana homogena i izotropno napeta, što ima za
posljedicu da napetost djeluje na rubu u smjeru vektora vanjske normale
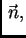 tj.
tj.
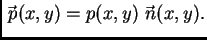 |
(2.47) |
U tom slučaju je matrica napetosti skalarna. Doista, iz (2.45),
(2.46) i (2.49) slijedi
Slično dobijemo
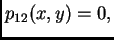
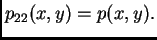 Dakle, u
tom slučaju je
Dakle, u
tom slučaju je
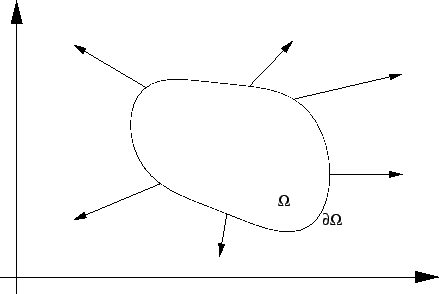
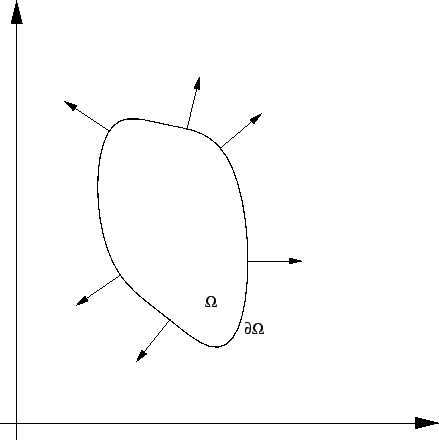
Ako je membrana u ravnoteži, onda je svaki njezin dio  u
ravnoteži. To znači da ukupna sila na rubu
u
ravnoteži. To znači da ukupna sila na rubu
 iščezava.
iščezava.
Odatle
 i i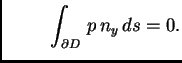 |
(2.48) |
Teorem o divergenciji u
 glasi
glasi
gdje je  područje u ravnini,
područje u ravnini,
 rub od
rub od
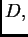 koji je po dijelovima glatka krivulja koja samu sebe ne
presijeca,
koji je po dijelovima glatka krivulja koja samu sebe ne
presijeca, 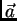 vektorsko polje klase
vektorsko polje klase 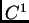 na nekoj okolini od
na nekoj okolini od
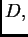 i
i 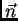 vektorsko polje vanjskih jediničnih normala
na
vektorsko polje vanjskih jediničnih normala
na
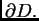
Specijalno, ako je
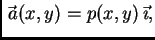 onda je
onda je
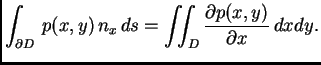 |
(2.49) |
Slično
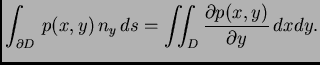 |
(2.50) |
Ove formule se zovu Gaussove formule.
Dakle, po teoremu o divergenciji, iz (2.50) slijedi
To vrijedi za
proizvoljni komad membrane  (područje u
(područje u  ), pa po osnovnoj
lemi zaključujemo da je
za svaki
), pa po osnovnoj
lemi zaključujemo da je
za svaki
 pa je prema tome
pa je prema tome
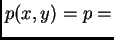
konst.
Osnovnim stanjem membrane smatrat ćemo ravnotežno stanje napete
membrane. Ako takvu membranu izvučemo iz položaja ravnoteže, ona se
počne gibati (oscilirati, titrati). Vektorska polja koja su nam pri
tom interesantna jesu
-
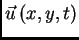 - progib membrane u točki
- progib membrane u točki 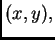 u čas
u čas
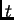 (polje pomaka),
(polje pomaka),
-
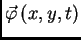 - količina gibanja membrane po
jedinici površine, u točki
- količina gibanja membrane po
jedinici površine, u točki 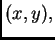 u čas
u čas 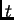 (površinska
gustoća količine gibanja),
(površinska
gustoća količine gibanja),
-
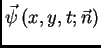 - količina gibanja, koja se u
jedinici vremena prenese kroz jedinični luk izvana prema unutra
(smjer suprotan smjeru jediničnog vektora vanjske normale
- količina gibanja, koja se u
jedinici vremena prenese kroz jedinični luk izvana prema unutra
(smjer suprotan smjeru jediničnog vektora vanjske normale 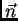 )
u točki
)
u točki 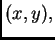 u čas
u čas 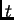 (linijska gustoća kontaktne
sile),
(linijska gustoća kontaktne
sile),
-
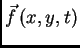 - količina gibanja po jedinici površine,
koja se u jedinici vremena izvana prenese na membranu u točki
- količina gibanja po jedinici površine,
koja se u jedinici vremena izvana prenese na membranu u točki
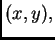 u čas
u čas 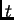 (površinska gustoća vanjske
sile).
(površinska gustoća vanjske
sile).
Polje
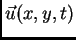 je kinematičko polje, a ostala tri polja su
dinamička.
je kinematičko polje, a ostala tri polja su
dinamička.
Subsections





Next: Zakon održanja.
Up: Rubni problemi
Previous: Rubni problemi
Sadržaj
Indeks
2001-10-26

![% latex2html id marker 36217
$\displaystyle \left[
\begin{array}{cc}
p_{11}(x,...
... p_{12}(x,y)\,n_y \\
p_{21}(x,y)\,n_x + p_{22}(x,y)\,n_y
\end{array}\right].$](img1974.png)
![]() tj.
tj.
![% latex2html id marker 36233
$\displaystyle {\cal P}(x,y) = \left[
\begin{array}{cc}
p(x,y) & 0 \\
0 & p(x,y)
\end{array}\right]$](img1982.png)
![]() u
ravnoteži. To znači da ukupna sila na rubu
u
ravnoteži. To znači da ukupna sila na rubu
![]() iščezava.
iščezava.
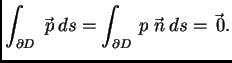
![]() glasi
glasi
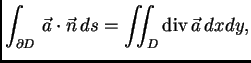
![]() onda je
onda je