




Next: Modifikacije Newtonove metode
Up: Rješavanje jednadžbi
Previous: Metoda iteracije
Sadržaj
Indeks
Newtonova metoda
Neka je
![$ f:[a,b]\rightarrow{}\mathbb{R}$](img2531.png) klase
klase 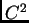 na
na ![$ [a,b].$](img2532.png) Želimo riješiti
jednadžbu
Želimo riješiti
jednadžbu
Newtonova metoda,
koja se često zove
Newton-Raphsonova metoda ili metoda
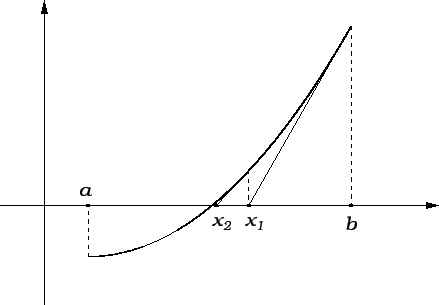
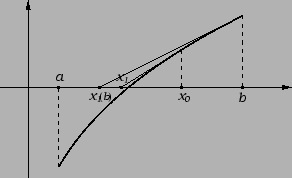
tangente, sastoji se u tome da se 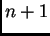 -va
aproksimacija
-va
aproksimacija 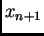 odredi kao sjecište tangente na graf
funkcije
odredi kao sjecište tangente na graf
funkcije 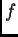 u točki s apscisom
u točki s apscisom 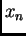 s osi
s osi 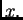
Jednadžba tangente na graf funkcije 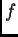 u točki
u točki
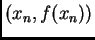 je
je
Kad stavimo 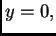 dobijemo njezino
sjecište s osi
dobijemo njezino
sjecište s osi 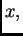 a to je
a to je 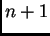 -va aproksimacija
-va aproksimacija 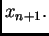 Dakle
Odatle slijedi
Dakle
Odatle slijedi
Time smo dobili sljedeći algoritam.
Algoritam 3
(Newtonova metoda)
Izaberemo
![$ x_0 \in [a,b],$](img2431.png)
i računamo niz
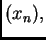
za
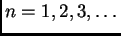
po formuli
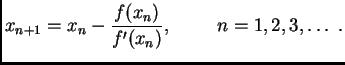 |
(3.8) |
Ako je
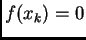
za neki
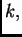
onda je
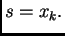
U protivnom
nastavljamo računanje daljnih članova niza.
Mathematica program 3
(Newtonova metoda)
f[t_]=; (* funkcija *)
x=; (* pocetna aproksimacija *)
n=0;
While[
N[f[x]]!=0.,
x=x-f[x]/f'[x];
n=n+1;
If[n>100,Break[]]; (* prekid nakon 100 iteracija *)
Print[N[x]]
]
Primjer 3.5
Newtonovom metodom riješiti jednadžbu iz primjera
3.1.
Rješenje. Pomoću programa 3 s početnom aproksimacijom
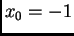 dobivamo
dobivamo
i to je sve,
jer se nakon 10 iteracija postiže strojna točnost. To pokazuje da
Newtonova metoda iteracije u ovom slučaju vrlo brzo konvergira.
Primjer 3.6
Riješiti problem iz primjera
3.2 Newtonovom metodom.
Rješenje. Pomoću programa 3 s početnom aproksimacijom
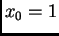 dobivamo
dobivamo
Program je napravljen tako da ponavlja iteracije 100 puta
ili završava postupak kad postigne strojnu točnost. Ovo pokazuje da
je u ovom primjeru strojna točnost postignuta već u četvrtoj
aproksimaciji.
S druge strane ako s istim programom (Newtonovom metodom) pokušamo
riješiti jednadžbu
počevši s 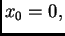 dobivamo
dobivamo
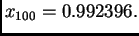 S sruge strane jasno je da je rješenje
S sruge strane jasno je da je rješenje 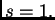 To pokazuje da
konvergencija nije uvijek tako brza kao u prethodnim
primjerima. Dapače, ako pokušamo na isti način riješiti jednadžbu
počevši s
To pokazuje da
konvergencija nije uvijek tako brza kao u prethodnim
primjerima. Dapače, ako pokušamo na isti način riješiti jednadžbu
počevši s 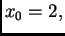 dobivamo redom
dobivamo redom
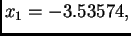
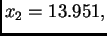
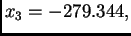
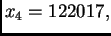
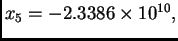 itd. Aproksimacije se sve više udaljavaju od rješenja koje je očito
itd. Aproksimacije se sve više udaljavaju od rješenja koje je očito
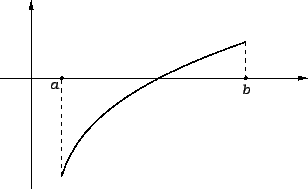
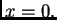 Sljedeći teorem je jedan od mnogih koji daju dovoljne uvjete
da Newtonova metoda konvergira. Uvjerite se da su uvjeti teorema
ispunjeni za primjer 3.5 na segmentu
Sljedeći teorem je jedan od mnogih koji daju dovoljne uvjete
da Newtonova metoda konvergira. Uvjerite se da su uvjeti teorema
ispunjeni za primjer 3.5 na segmentu ![$ [-2,-1].$](img2562.png)
Primjer 3.7
Neka je
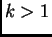
prirodan broj, i neka je
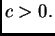
Nađimo, pomoću Newtonove metode, približnu vrijednost pozitivnog
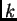
-tog korijena iz
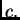
Rješenje. Izračunati 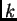 -ti
korijen iz broja
-ti
korijen iz broja 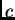 znači riješiti po
znači riješiti po 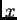 jednadžbu
jednadžbu
Ovdje je
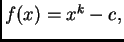
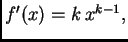
pa
Newtonova metoda daje
odnosno
Što se tiče izbora početne aproksimacije 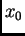 i konvergencije,
primijetimo sljedeće. Za
i konvergencije,
primijetimo sljedeće. Za
![$ 0<a<\sqrt[k]{c}<b$](img2620.png) imamo
imamo
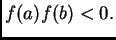 Zatim, zbog
Zatim, zbog
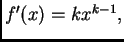
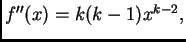 za svaki
za svaki
![$ x \in
[a,b]$](img2624.png) je
je 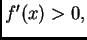 i
i 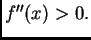 Na kraju, iz pozitivnosti
funkcije
Na kraju, iz pozitivnosti
funkcije 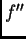 slijedi rast funkcije
slijedi rast funkcije 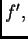 pa je
pa je 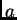 onaj rub segmenta
u kojem
onaj rub segmenta
u kojem 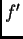 ima manju vrijednost. Da bi vrijedilo
ima manju vrijednost. Da bi vrijedilo
mora biti
Dakle za tako veliki
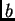
ispunjeni su svi uvjeti teorema
24. Kako
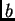
smijemo uzeti još veći, i kako
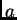
može biti bilo koji broj veći od
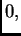
i manji od
![$ \sqrt[k]{c},$](img2630.png)
slijedi da postupak konvergira za svaki
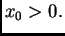
U programskom paketu Mathematica se ovaj postupak programira
vrlo jednostavno
Mathematica program 4
(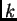 -ti korijen)
-ti korijen)
Map[Nest[((k-1) # + c/#^(k-1))/k&,x0,#1]&,Range[p]]//N
gdje je
p broj aproksimacija koje želimo, a broj
x0 je
početna aproksimacija. Naravno
k je broj korijena koji se
vadi.
Specijalno kad je 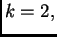 imamo jednostavnu i vrlo efikasnu formulu za
približno računanje drugog korijena
imamo jednostavnu i vrlo efikasnu formulu za
približno računanje drugog korijena
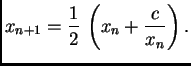 |
(3.10) |
Uvjerite se na primjerima kako je formula za računanje drugog
korijena efikasna.
Primjer 3.8
Za dani pozitivan broj
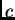
naći približnu vrijednost njemu
recipročnog broja bez dijeljenja.
Rješenje. To je isto kao približno riješiti jednadžbu
Newtonova metoda daje
U ovoj formuli nema dijeljenja, i mi smo riješili zadatak, ako
postoji interval u kojem možemo birati početnu aproksimaciju tako
da ovaj postupak konvergira. Ispitajmo uvjete teorema
24 u ovom slučaju.
Neka su sada
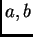
takvi da je
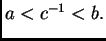
Time je uvjet
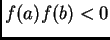
ispunjen. Iz pozitivnosti
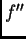
slijedi da
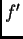
raste. No
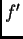
ima negativne vrijednosti, pa iz
rasta
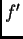
slijedi da
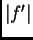
pada. Tako
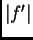
prima manju vrijednost
u rubnoj točki
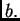
pa
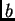
određujemo iz kvadratne nejednadžbe
Izlazi da se
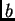
mora nalaziti između
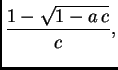
i
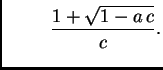
Budući da
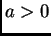
možemo uzeti po volji malen, slijedi da se za
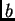
može uzeti bilo koji broj manji od
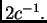
Tako se za početnu
aproksimaciju može uzeti bilo koji
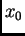
takav da je
Ako želimo ocijeniti grešku, primijetimo da je Newtonova metoda
zapravo metoda iteracije, ako stavimo
Tada je
Neka je
Tada je apriorna ocjena greške dana formulom (3.6), a
aposteriorna formulom (3.7).
Primjer 3.9
Naći
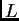
u slučaju približnog računanja drugog korijena po
formuli (
3.10).
Rješenje. Treba naći približnu vrijednost od 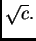 Neka je
Neka je
Prirodno je početnu aproksimaciju uzeti u segmentu
![$ [n,n+1].$](img2654.png)
Tada je
U ovom slučaju je
pa je
Odavde se vidi da je uvijek
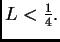
Subsections





Next: Modifikacije Newtonove metode
Up: Rješavanje jednadžbi
Previous: Metoda iteracije
Sadržaj
Indeks
2001-10-26
![]() klase
klase ![]() na
na ![]() Želimo riješiti
jednadžbu
Želimo riješiti
jednadžbu
![]() -va
aproksimacija
-va
aproksimacija ![]() odredi kao sjecište tangente na graf
funkcije
odredi kao sjecište tangente na graf
funkcije ![]() u točki s apscisom
u točki s apscisom ![]() s osi
s osi ![]()
![]() u točki
u točki
![]() je
je
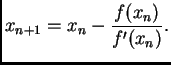
![]() dobivamo
dobivamo
![]() dobivamo
dobivamo
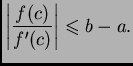
![]() za
bilo koju početnu aproksimaciju
za
bilo koju početnu aproksimaciju
![]()
![$\displaystyle f(x) = f(\xi)+f'(\xi)\,(x-\xi)+\frac{f''(x_{\xi})}{2!}\,(x-\xi),\hspace{1cm}
\forall{}x\in[a,b],$](img2583.png)
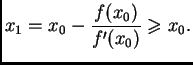
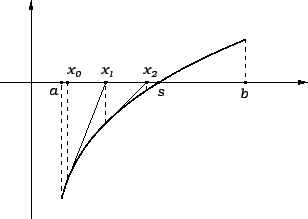
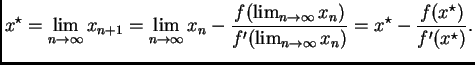
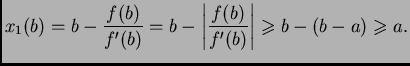
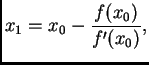
![]() -ti
korijen iz broja
-ti
korijen iz broja ![]() znači riješiti po
znači riješiti po ![]() jednadžbu
jednadžbu
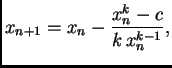
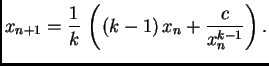
![]() i konvergencije,
primijetimo sljedeće. Za
i konvergencije,
primijetimo sljedeće. Za
![]() imamo
imamo
![]() Zatim, zbog
Zatim, zbog
![]()
![]() za svaki
za svaki
![]() je
je ![]() i
i ![]() Na kraju, iz pozitivnosti
funkcije
Na kraju, iz pozitivnosti
funkcije ![]() slijedi rast funkcije
slijedi rast funkcije ![]() pa je
pa je ![]() onaj rub segmenta
u kojem
onaj rub segmenta
u kojem ![]() ima manju vrijednost. Da bi vrijedilo
ima manju vrijednost. Da bi vrijedilo
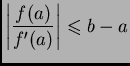
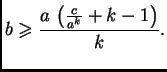
![]() imamo jednostavnu i vrlo efikasnu formulu za
približno računanje drugog korijena
imamo jednostavnu i vrlo efikasnu formulu za
približno računanje drugog korijena
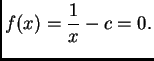
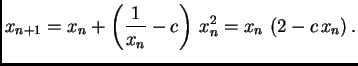
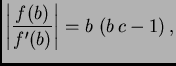
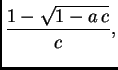 i
i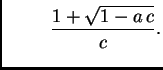
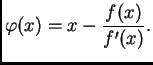
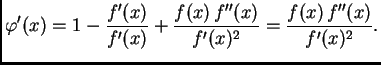
![$\displaystyle \left\vert\frac{f(x)\,f''(x)}{f'(x)^2}\right\vert\leqslant L < 1,\hspace{1cm}\forall x \in
[a,b].$](img2650.png)
![]() Neka je
Neka je
![$\displaystyle L \leqslant{} \max{}\left\vert\frac{f(x)\,f''(x)}{f'(x)^2}\right\vert, \quad
\forall{}x \in [n,n+1].$](img2655.png)
![$\displaystyle L \leqslant{} \max_{x \in [n,n+1]}\left\vert\frac{x^2-c}{4\,x^2}\...
...ght\vert
\leqslant{} \frac{1}{4}\,\left\vert 1 - \frac{n}{(n+1)^2}\right\vert.$](img2657.png)