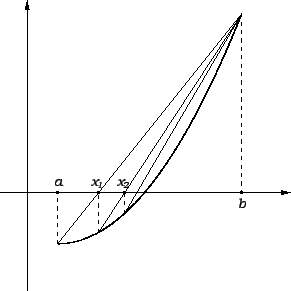

Ideja metode je da se ![]() -va aproksimacija odredi kao sjecište osi
-va aproksimacija odredi kao sjecište osi
![]() i sekante kroz točke na grafu funkcije
i sekante kroz točke na grafu funkcije ![]() čije apscise su
prethodne aproksimacije takve, da su vrijednosti funkcije u njima
različitog znaka. Dakle, možemo koristiti Newtonovu metodu u kojoj
čije apscise su
prethodne aproksimacije takve, da su vrijednosti funkcije u njima
različitog znaka. Dakle, možemo koristiti Newtonovu metodu u kojoj
![]() zamjenimo s koeficijentom sekante
zamjenimo s koeficijentom sekante
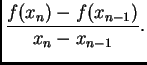
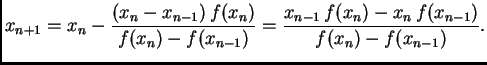
Tako imamo sljedeći algoritam.
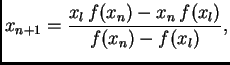
f[t_]=; (* funkcija *)
a=;
b=; (* pocetni interval (zadati kao realne brojeve) *)
If[f[a]f[b]<=0,
x=(a f[b]-b f[a])/(f[b]-f[a]);
n=0;
Print[{" ",n,N[a],N[x],N[b]}];
While[N[f[x]]!=0.,
Print[N[f[a]]," ",N[f[x]]," ",N[f[b]]];
If[
f[b]f[x]<0,
a=x;x=N[(x f[b]-b f[x])/(f[b]-f[x])],
b=x;x=N[(a f[x]-x f[a])/(f[x]-f[a])]
];
n=n+1;
If[n>100,Break[]];
Print[{" ",n,N[a],N[x],N[b]}]],"Na odabranom segmentu
nije ispunjen nuzan uvjet postojanja rjesenja"]
Metoda uvijek konvergira. Konvergencija je brža nego kod metode polovljenja, ali sporija nego kod Newtonove metode.