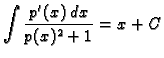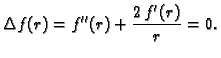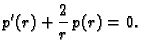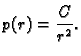Next: Linearna diferencijalna jednadžba 2.
Up: Obične diferencijalne jednadžbe
Previous: Metoda separacije varijabli
Contents
Index
Subsections
Diferencijalna jednadžba 1. reda kod koje desna strana ima oblik
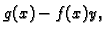 tj. koja se može svesti na oblik
tj. koja se može svesti na oblik
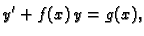 |
(6.14) |
gdje su
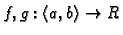 neprekidne funkcije na
neprekidne funkcije na
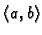 zove se linearna diferencijalna jednadžba 1.
reda. Ako je
zove se linearna diferencijalna jednadžba 1.
reda. Ako je 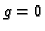 onda je jednadžba (6.14) homogena, u
protivnom nehomogena.
onda je jednadžba (6.14) homogena, u
protivnom nehomogena.
Teorem 27
Neka su
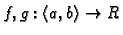
neprekidne funkcije. Tada
za svaki
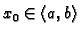
i
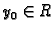
postoji jedno i samo
jedno rješenje Cauchyjevog problema
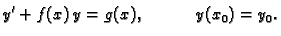 |
(6.15) |
Slika 6.5:
Područje početnog uvjeta za linearnu diferencijalnu jednadžbu.
|
|
Dokaz. Dokaz provodimo tako da najprije riješimo
pripadnu homogenu jednadžbu. Pripadna homogena se može napisati u
obliku
pa možemo primijeniti metodu separacije varijabli
(v. teorem 25). Funkcije 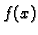 i
i 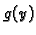 iz separacije
varijabli sada su
iz separacije
varijabli sada su 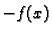 i
i 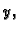 pa su primitivne od
pa su primitivne od 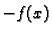 i
i
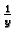 Slijedi
Odatle po formuli (6.7),
Time smo riješili Cauchyjev problem za pripadnu
homogenu jednadžbu.6.1 Opće rješenje pripadne homogene jednadžbe
je
Slijedi
Odatle po formuli (6.7),
Time smo riješili Cauchyjev problem za pripadnu
homogenu jednadžbu.6.1 Opće rješenje pripadne homogene jednadžbe
je
Rješenje nehomogene jednadžbe tražimo u obliku
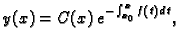 |
(6.16) |
tj. pretpostavkom da je 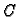 funkcija od
funkcija od 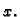 Ta ideja se zove
variranje konstante. Uvrstimo li (6.16) u
(6.15), dobivamo
tj.
Tako je
Dakle, opće rješenje nehomogene jednadžbe je
Ta ideja se zove
variranje konstante. Uvrstimo li (6.16) u
(6.15), dobivamo
tj.
Tako je
Dakle, opće rješenje nehomogene jednadžbe je
Što se tiče rješenja Cauchyjevog problema, primijetimo da je
Tako rješenje Cauchyjevog problema glasi
Prvi sumand na desnoj strani je rješenje pripadne homogene jednadžbe uz
početni uvjet
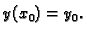 Uvrštavanjem se lako provjeri da drugi sumand
rješava nehomogenu jednadžbu (6.14).
Uvrštavanjem se lako provjeri da drugi sumand
rješava nehomogenu jednadžbu (6.14).

Primjer 6.5
Bernoullijeva jednadžba ima oblik
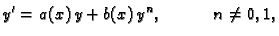 |
(6.17) |
gdje su
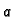
i
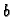
neprekidne funkcije na nekom intervalu
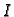
.
Rješenje. Ova jednadžba se svodi na linearnu supstitucijom
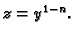 Zaista,
Zaista,
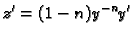 i ako jednadžbu (6.17) množimo s
i ako jednadžbu (6.17) množimo s
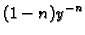 dobivamo
dobivamo
gdje je
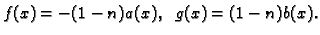
Neka je  konveksan skup 1.1.1 u
konveksan skup 1.1.1 u 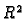 ,
,
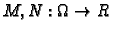 funkcije klase
funkcije klase
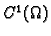 i
i
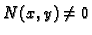 za
za
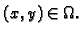 Diferencijalna jednadžba 1. reda
Diferencijalna jednadžba 1. reda
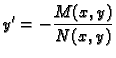 |
(6.18) |
se zove egzaktna, ako je
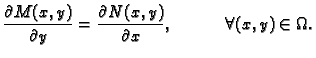 |
(6.19) |
Uvrštavajući (6.18) u formulu za diferencijal
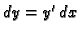 funkcije
funkcije 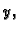 dobivamo
Odatle
dobivamo
Odatle
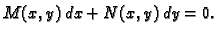 |
(6.20) |
Tako (6.18) i (6.20) predstavljaju dva zapisa
jedne te iste diferencijalne jednadžbe.
Uvjet (6.19), koji se inače zove uvjet egzaktnosti, predstavlja za vektorsku funkciju
uvjet
To znači da je vektorsko polje potencijalno, tj. da postoji skalarno
polje (potencijal) 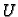 takvo, da je
i ono se računa po formuli
pri čemu je
Ako to uvrstimo u jednadžbu (6.20) imamo
To
znači da je derivacija (diferencijal)
takvo, da je
i ono se računa po formuli
pri čemu je
Ako to uvrstimo u jednadžbu (6.20) imamo
To
znači da je derivacija (diferencijal)
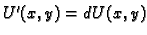 funkcije
funkcije 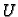 jednak nuli (nulfunkciji, v. def. 12) za svaki
jednak nuli (nulfunkciji, v. def. 12) za svaki
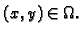 Odatle slijedi da su parcijalne derivacije funkcije
Odatle slijedi da su parcijalne derivacije funkcije
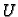 jednake nuli za svaki
jednake nuli za svaki
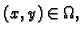 pa je prema tome
pa je prema tome 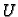 konstanta. Doista, za
konstanta. Doista, za
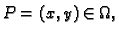 po teoremu srednje
vrijednosti, imamo
gdje je
po teoremu srednje
vrijednosti, imamo
gdje je 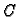 točka na spojnici točaka
točka na spojnici točaka
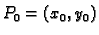 i
i 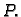 Tako je
Tako je
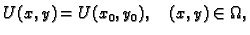 |
(6.21) |
tj. 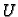 je konstanta.
je konstanta.
Prema tome
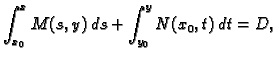 |
(6.22) |
gdje je  neka konstanta. Ovom jednadžbom je implicitno zadana
funkcija
neka konstanta. Ovom jednadžbom je implicitno zadana
funkcija 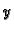 kao funkcija od
kao funkcija od 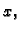 koja zadovoljava jednadžbu
(6.20), što znači da smo formulom
(6.22) dobili implicitno zadano opće rješenje
egzaktne diferencijalne jednadžbe (v. 1.4.3).
koja zadovoljava jednadžbu
(6.20), što znači da smo formulom
(6.22) dobili implicitno zadano opće rješenje
egzaktne diferencijalne jednadžbe (v. 1.4.3).
Cauchyjev problem za ovu diferencijalnu jednadžbu glasi: za danu
točku
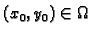 naći funkciju
naći funkciju 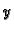 takvu da zadovoljava
takvu da zadovoljava
Da bismo našli
rješenje Cauchyjevog problema dovoljno je primijetiti da
uvrštavanjem
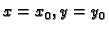 u opće rješenje slijedi
u opće rješenje slijedi 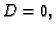 i prema
tome
i prema
tome
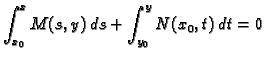 |
(6.23) |
je implicitno zadano rješenje Cauchyjevog problema.
Time je dokazan sljedeći teorem.
Teorem 28
Neka je

konveksno područje u
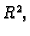
neka su
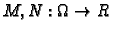
funkcije klase
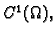
neka je
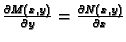
i
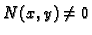
za
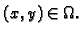
Tada za svaki
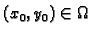
Cauchyjev problem
ima jedno i samo jedno rješenje.
Primjer 6.6
Treba riješiti Cauchyjev problem
Rješenje. Uvjet
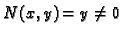 pokazuje da
pokazuje da  ne smije sjeći os
ne smije sjeći os
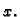 Odatle nužno mora biti
Odatle nužno mora biti
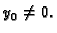 Uzmimo da je
Uzmimo da je 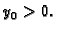 To
znači da za
To
znači da za  možemo uzeti gornju poluravninu. Lako se
provjeri da je jednadžba egzaktna. Po formuli (6.23)
možemo uzeti gornju poluravninu. Lako se
provjeri da je jednadžba egzaktna. Po formuli (6.23)
Dakle, rješenje Cauchyjevog problema je
odnosno
Slika 6.6:
Rješenje Cauchyjevog problema.
|
|
Opće rješenje diferencijalne jednadžbe je
Obzirom na odabrani

u obzir dolaze samo polukružnice u gornjoj poluravnini.
Primjer 6.7
Treba riješiti jednadžbu
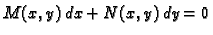 |
(6.24) |
u kojoj
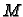
i
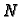
ne zadovoljavaju
uvjet egzaktnosti (
6.19).
Rješenje. Množimo (6.24) s funkcijom 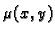 takvom da
dobivena jednadžba
takvom da
dobivena jednadžba
bude egzaktna, tj. da vrijedi
Odatle dobivamo uvjet za funkciju
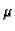
.
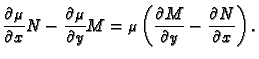 |
(6.25) |
Ovaj uvjet na funkciju
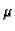
je parcijalna diferencijalna jednadžba
i općenito teže ju je riješiti nego početnu (
6.24).
Zato pokušavamo s jednostavnijom pretpostavkom
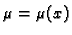
ili
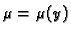
ili
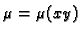
i slično. Tada se uvjet
(
6.25) pojednostavnjuje. Na pr. ako je
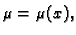
onda je (
6.25)
To je linearna homogena diferencijalna jednadžba i rješenje je
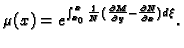 |
(6.26) |
Ova pretpostavka na
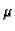
vrijedi ako je
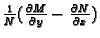
funkcija samo od

jer je tada na desnoj strani formule (
6.26) funkcija samo
od

.
Funkcija 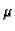 se zove Eulerov multiplikator.
se zove Eulerov multiplikator.
Primjer 6.8
Jednadžba
očito nije egzaktna. Riješimo je.
Rješenje.
Tako možemo izabrati
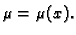
Lako se vidi da je
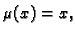
pa dolazimo do jednadžbe
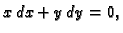
što je egzaktna jednadžba, koju
smo već riješili.
Neka je
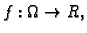 neprekidna funkcija na području
neprekidna funkcija na području
 u
u 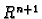 . Jednadžbu
. Jednadžbu
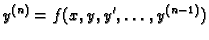 |
(6.27) |
zovemo običnom diferencijalnom jednadžbom n-tog reda.
a) Pretpostavimo da u diferencijalnoj jednadžbi (6.27) ne
dolazi eksplicitno 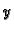 , tj. da imamo
, tj. da imamo
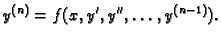 |
(6.28) |
Stavimo
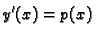 |
(6.29) |
Odatle
Uvrstimo u (6.28), dobivamo
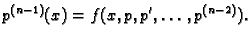 |
(6.30) |
Time smo snizili red diferencijalne jednadžbe, jer je jednadžba
(6.30) 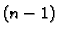 -og reda. Ako je
-og reda. Ako je 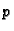 rješenje jednadžbe
(6.30) onda jednostavnom integracijom dobivamo iz
(6.29) rješenje jednadžbe (6.28).
rješenje jednadžbe
(6.30) onda jednostavnom integracijom dobivamo iz
(6.29) rješenje jednadžbe (6.28).
b) Pretpostavimo da u jednadžbi (6.27) ne dolazi  eksplicitno, tj. da je
eksplicitno, tj. da je
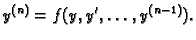 |
(6.31) |
Stavimo
Tada je
Općenito je 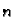 -ta derivacija
-ta derivacija 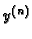 funkcija od
funkcija od
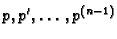 .
Uvrštavanjem u (6.31) dobivamo tako diferencijalnu jednadžbu
.
Uvrštavanjem u (6.31) dobivamo tako diferencijalnu jednadžbu
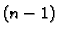 -og reda.
-og reda.
Primjer 6.9
Treba naći opće rješenje jednadžbe
Rješenje. U ovoj diferencijalnoj jednadžbi se ne pojavljuju ni  ni
ni 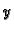 .
Stavimo
.
Stavimo
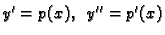 . Dobivamo
. Dobivamo
- 1.
- Koju diferencijalnu jednadžbu zovemo linearnom diferencijalnom
jednadžbom 1. reda? Kad kažemo da je homogena, a kad da je
nehomogena?
- 2.
- Što znate o postojanju i jedinstvenosti rješenja? Kako se
rješava linearna diferencijalna jednadžba 1. reda?
- 3.
- Koja je razlika između pojmova homogenosti kad se radi o običnoj
diferencijalnoj jednadžbi 1. reda, i linearnoj diferencijalnoj
jednadžbi 1. reda?
- 4.
- Kako glasi Bernoullijeva jednadžba? Kako se rješava?
- 5.
- Kako izgleda egzaktna diferencijalna jednadžba? Kako glasi
njezino rješenje?
- 6.
- U čemu je osobitost rješenja egzaktne diferencijalne jednadžbe?
Da li znate izvesti rješenje?
- 7.
- Kako se diferencijalna jednadžba može svesti na egzaktnu? Što
je to Eulerov multiplikator. U kojim slučajevima taj postupak može
pojednostavniti rješavanje?
- 8.
- Kako izgleda obična diferencijalna jednadžba
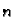 -tog reda?
-tog reda?
- 9.
- U kojim slučajevima se može sniziti red jednadžbe? Kako se to
radi?
- 1.
- Naći opće rješenje Laplaceove jednadžbe
gdje je
 dvaput neprekidno derivabilna funkcija, a
dvaput neprekidno derivabilna funkcija, a
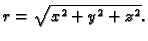
Rješenje. Iz primjera (4.14) imamo
Budući da se u ovoj jednadžbi ne pojavljuje eksplicitno 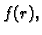 možemo staviti
možemo staviti
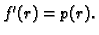 Tada jednadžba postaje
Ovo je homogena linearna diferencijalna jednadžba i njezino rješenje
je
Odatle je
Tada jednadžba postaje
Ovo je homogena linearna diferencijalna jednadžba i njezino rješenje
je
Odatle je





Next: Linearna diferencijalna jednadžba 2.
Up: Obične diferencijalne jednadžbe
Previous: Metoda separacije varijabli
Contents
Index
Salih Suljagic
2000-03-11
![]() tj. koja se može svesti na oblik
tj. koja se može svesti na oblik
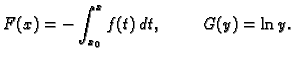
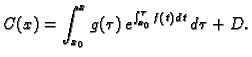
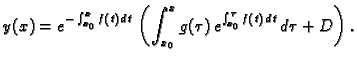
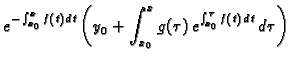
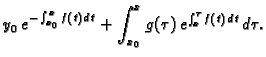
![]() Zaista,
Zaista,
![]() i ako jednadžbu (6.17) množimo s
i ako jednadžbu (6.17) množimo s
![]() dobivamo
dobivamo
![]() konveksan skup 1.1.1 u
konveksan skup 1.1.1 u ![]() ,
,
![]() funkcije klase
funkcije klase
![]() i
i
![]() za
za
![]() Diferencijalna jednadžba 1. reda
Diferencijalna jednadžba 1. reda
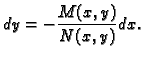
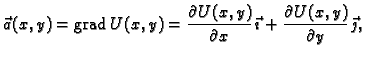
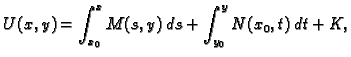
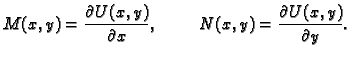
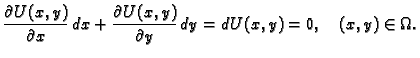
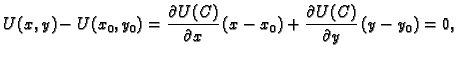
![]() naći funkciju
naći funkciju ![]() takvu da zadovoljava
takvu da zadovoljava
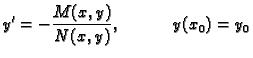
![]() pokazuje da
pokazuje da ![]() ne smije sjeći os
ne smije sjeći os
![]() Odatle nužno mora biti
Odatle nužno mora biti
![]() Uzmimo da je
Uzmimo da je ![]() To
znači da za
To
znači da za ![]() možemo uzeti gornju poluravninu. Lako se
provjeri da je jednadžba egzaktna. Po formuli (6.23)
možemo uzeti gornju poluravninu. Lako se
provjeri da je jednadžba egzaktna. Po formuli (6.23)
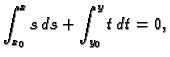
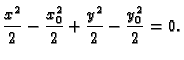
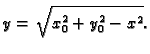
![]() takvom da
dobivena jednadžba
takvom da
dobivena jednadžba
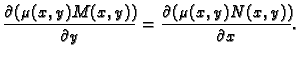
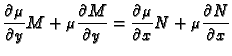
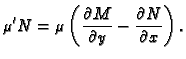
![]() se zove Eulerov multiplikator.
se zove Eulerov multiplikator.
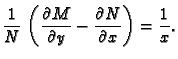
![]() neprekidna funkcija na području
neprekidna funkcija na području
![]() u
u ![]() . Jednadžbu
. Jednadžbu
![]() , tj. da imamo
, tj. da imamo
![]() eksplicitno, tj. da je
eksplicitno, tj. da je
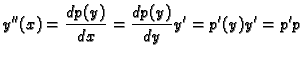
![]() ni
ni ![]() .
Stavimo
.
Stavimo
![]() . Dobivamo
. Dobivamo