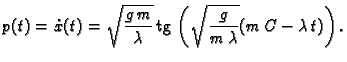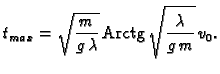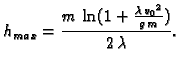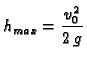Next: Linearne jednadžbe višeg reda
Up: Obične diferencijalne jednadžbe
Previous: Linearna diferencijalna jednadžba 1.
Contents
Index
Subsections
Neka je
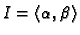 ,
,
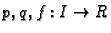 neprekidne funkcije na
neprekidne funkcije na 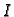 i
i 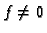 , tj.
, tj.
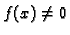 za bar jedan
za bar jedan
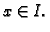 Tada jednadžbu
Tada jednadžbu
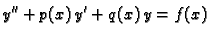 |
(6.32) |
zovemo nehomogenom linearnom diferencijalnom jednadžbom 2. reda.
Jednadžbu
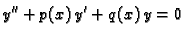 |
(6.33) |
zovemo pripadnom homogenom jednadžbom.
Teorem 29
Neka su
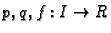
neprekidne funkcije na
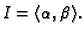
Označimo s
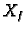
skup svih rješenja
nehomogene jednadžbe, a s
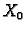
skup svih rješenja pripadne
homogene jednadžbe. Neka je
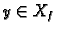
proizvoljan. Tada je
- 1.
-
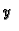 klase
klase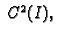
- 2.
-
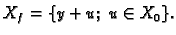
Dokaz. i).
pa iz neprekidnosti funkcija
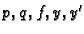 slijedi neprekidnost
slijedi neprekidnost 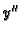 , tj.
, tj.
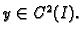 6.2
6.2
ii). Ako je 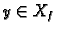 i
i 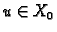 , onda je
, onda je
pa je
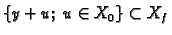 .
.
Obratno, neka je 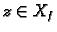 .
Stavimo
.
Stavimo 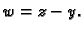
pa je 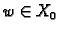 i
i 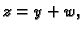 tj.
tj.
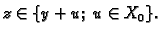 Odatle
imamo suprotnu inkluziju,
Odatle
imamo suprotnu inkluziju,
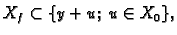 pa je
dakle
i time je teorem dokazan.
pa je
dakle
i time je teorem dokazan.

Teorem 30
Neka je
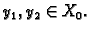
Tada je
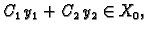
za proizvoljne konstante
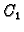
i
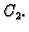
Dokaz. Ako je
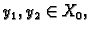 onda to
znači da
onda to
znači da 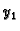 i
i 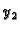 rješavaju pripadnu homogenu jednadžbu. Tada
rješavaju pripadnu homogenu jednadžbu. Tada
Prema tome i
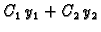 rješava pripadnu homogenu
jednadžbu, tj.
rješava pripadnu homogenu
jednadžbu, tj.
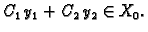

Teorem 31
Neka su
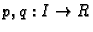
neprekidne funkcije na intervalu
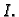
Tada
- 1.
- za svaki
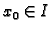 i za svaki
i za svaki 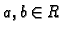 Cauchyjev problem
Cauchyjev problem
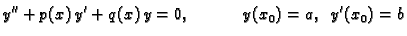 |
(6.34) |
ima jedno i samo jedno rješenje;
- 2.
- skup
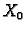 svih rješenja pripadne homogene diferencijalne
jednadžbe je dvodimenzionalni vektorski prostor.
svih rješenja pripadne homogene diferencijalne
jednadžbe je dvodimenzionalni vektorski prostor.
Primijetimo da iz prve tvrdnje slijedi druga. U tu svrhu dovoljno je
uočiti da je skup svih početnih uvjeta, koji figuriraju u Cauchyjevom
problemu, dvodimenzionalni vektorski prostor, ako početni uvjet
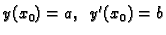 shvatimo kao uređen par
shvatimo kao uređen par 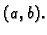 Tada je,
naime,
Tada je,
naime,
Dakle, svaki početni uvjet je linearna kombinacija dva linearno
nezavisna početna uvjeta 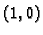 i
i 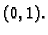
Posljedica ovog teorema jeste da je
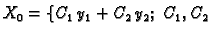
proizvoljne konstante
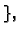
tj. opće rješenje homogene linearne diferencijalne jednadžbe 2. reda je
gdje su 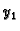 i
i 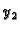 dva linearno nezavisna rješenja homogene
jednadžbe. Ako su poznata dva rješenja, provjeriti da li su linearno
nezavisna može se na sljedeći način.
dva linearno nezavisna rješenja homogene
jednadžbe. Ako su poznata dva rješenja, provjeriti da li su linearno
nezavisna može se na sljedeći način.
Teorem 32
Neka su
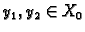
i
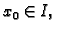
i neka je
Tada su sljedeće tvrdnje
ekvivalentne.
- 1.
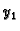 i
i 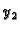 su linearno nezavisne.
su linearno nezavisne.
- 2.
-
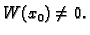
- 3.
-
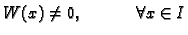 .
.
Realna funkcija
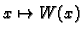 definirana na
definirana na 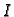 se zove
Wronskijan ili determinanta Wronskog.
se zove
Wronskijan ili determinanta Wronskog.
Proizvoljna baza u vektorskom prostoru 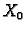 se zove fundamentalni sustav rješenja homogene jednadžbe. Iz prethodnog
teorema vidimo da će uređeni par rješenja
se zove fundamentalni sustav rješenja homogene jednadžbe. Iz prethodnog
teorema vidimo da će uređeni par rješenja 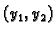 biti
fundamentalni sustav rješenja ako i samo ako je
biti
fundamentalni sustav rješenja ako i samo ako je
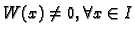 , a za to je dovoljno provjeriti da je
, a za to je dovoljno provjeriti da je
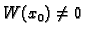 za
barem jedan
za
barem jedan 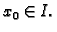
Budući da se svako rješenje pripadne homogene jednadžbe može dobiti kao
linearna kombinacija dva linearno nezavisna rješenja, opće rješenje
nehomogene jednadžbe ćemo moći napisati ako znamo dva
linearno nezavisna rješenja homogene jednadžbe i jedno partikularno
rješenje nehomogene jednadžbe. Tako je opće rješenje nehomogene
jednadžbe oblika
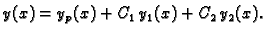 |
(6.35) |
Zahvaljujući prethodnim razmatranjima u rješavanju nehomogene
jednadžbe bitnu ulogu ima nalaženje fundamentalnog sustava rješenja
pripadne homogene jednadžbe. To je u pravilu težak problem. Ipak, ako su
koeficijenti jednadžbe 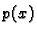 i
i 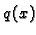 konstante, onda je taj problem
jednostavno rješiv.
konstante, onda je taj problem
jednostavno rješiv.
Teorem 33
Neka su
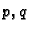
konstante i neka je dana jednadžba
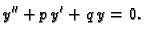 |
(6.36) |
Neka su
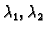
rješenja jednadžbe
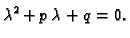 |
(6.37) |
1. Ako je
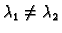
onda funkcije
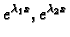
čine fundamentalni sustav rješenja jednadžbe
(
6.36).
2. Ako je
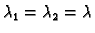 jedno dvostruko rješenje
jednadžbe (6.37), onda funkcije
jedno dvostruko rješenje
jednadžbe (6.37), onda funkcije
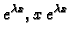 čine fundamentalni sustav rješenja
jednadžbe (6.36).
čine fundamentalni sustav rješenja
jednadžbe (6.36).
Dokaz. 1. Jednadžba
se zove karakteristična jednadžba. Do nje dolazimo tako da
pretpostavimo rješenje u obliku
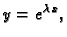 i uvrstimo ga u
jednadžbu. Dobivamo
Kako je
i uvrstimo ga u
jednadžbu. Dobivamo
Kako je
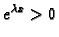 za bilo koji
za bilo koji
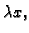 slijedi
Neka su
slijedi
Neka su 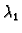 i
i 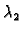 dva međusobno različita rješenja
karakteristične jednadžbe. Tada funkcije
dva međusobno različita rješenja
karakteristične jednadžbe. Tada funkcije
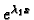 i
i
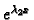 rješavaju homogenu jednadžbu, i
pa je
i tako je
rješavaju homogenu jednadžbu, i
pa je
i tako je
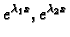 zaista fundamentalni sustav
rješenja jednadžbe (6.36).
zaista fundamentalni sustav
rješenja jednadžbe (6.36).
2. Kao u 1. imamo da je
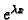 rješenje jednadžbe (6.36).
Stavimo
rješenje jednadžbe (6.36).
Stavimo
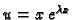 .
.
Uvrstimo u (6.36).
Budući da je 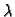 dvostruko rješenje jednadžbe (6.37),
slijedi
Odatle slijedi
pa je
dvostruko rješenje jednadžbe (6.37),
slijedi
Odatle slijedi
pa je 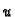 također rješenje jednadžbe (6.36). Nadalje
pa je
i tako je
također rješenje jednadžbe (6.36). Nadalje
pa je
i tako je
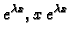 zaista fundamentalni sustav
rješenja jednadžbe (6.36).
zaista fundamentalni sustav
rješenja jednadžbe (6.36).

Ovaj teorem nam daje metodu za rješavanje homogene linearne diferencijalne
jednadžbe 2. reda s konstantnim koeficijentima. Algebarska jednadžba
(6.37) drugog stupnja se zove karakteristična jednadžba, a
polinom na lijevoj strani jednadžbe (6.37) karakteristični
polinom diferencijalne jednadžbe (6.36).
Primjer 6.10
Treba naći opće rješenje jednadžbe
Rješenje.
Dakle, opće rješenje je
Zbog fizikalnih razloga se funkcija  na desnoj strani linearne
diferencijalne jednadžbe
na desnoj strani linearne
diferencijalne jednadžbe
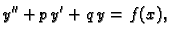 |
(6.38) |
zove funkcija smetnje. U nekim se slučajevima iz tipa
funkcije  može zaključiti kojeg je oblika partikularno
rješenje.
može zaključiti kojeg je oblika partikularno
rješenje.
a) Neka je
polinom stupnja 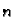 . Budući da je linearna kombinacija derivacija polinoma
opet polinom, pretpostavljamo
. Budući da je linearna kombinacija derivacija polinoma
opet polinom, pretpostavljamo
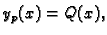 |
(6.39) |
gdje je 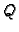 polinom s nepoznatim koeficijentima. Da bismo odredili
koeficijente uvrstimo
polinom s nepoznatim koeficijentima. Da bismo odredili
koeficijente uvrstimo 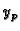 u diferencijalnu jednadžbu.
u diferencijalnu jednadžbu.
Ako je 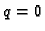 , onda je
, onda je
Ako je 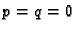 , onda je
, onda je
b) Neka je
Budući da su derivacije od 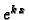 funkcije istog tipa, pretpostavimo
Uvrštavanjem
funkcije istog tipa, pretpostavimo
Uvrštavanjem 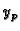 u diferencijalnu jednadžbu određuje se
u diferencijalnu jednadžbu određuje se 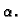
Ako je 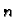 jednostruki korijen karakterističnog polinoma, onda
pretpostavljamo
jednostruki korijen karakterističnog polinoma, onda
pretpostavljamo
Ako je 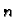 dvostruki korijen karakterističnog polinoma, onda pretpostavljamo
dvostruki korijen karakterističnog polinoma, onda pretpostavljamo
c) Neka je
gdje je 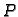 neki polinom. Derivacije ove funkcije su opet funkcije istog
tipa. Zato pretpostavljamo
gdje je
neki polinom. Derivacije ove funkcije su opet funkcije istog
tipa. Zato pretpostavljamo
gdje je 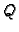 polinom istog stupnja kao
polinom istog stupnja kao 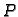 .
.
Ako je 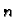 jednostruki korijen karakterističnog polinoma, onda
jednostruki korijen karakterističnog polinoma, onda
Ako je 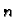 dvostruki korijen karakterističnog polinoma, onda
dvostruki korijen karakterističnog polinoma, onda
d) Neka je
Budući da su derivacije od  funkcije istog tipa, pretpostavljamo
Ako je
funkcije istog tipa, pretpostavljamo
Ako je 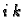 korijen karakterističnog polinoma, onda pretpostavljamo
korijen karakterističnog polinoma, onda pretpostavljamo
e) Ako je
gdje su 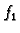 i
i 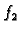 funkcije nekih od gore navedenih tipova, onda se
rješenje traži u obliku linearne kombinacije odgovarajućih partikularnih
rješenja.
funkcije nekih od gore navedenih tipova, onda se
rješenje traži u obliku linearne kombinacije odgovarajućih partikularnih
rješenja.
Primjer 6.11
Naći opće rješenje jednadžbe
Rješenje. Desnu stranu jednadžbe možemo napisati drugačije
Korijeni karakterističnog polinoma su
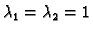
. Tako
pretpostavljamo
Izlazi
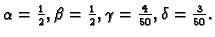
Tako je
odnosno opće rješenje je
- 1.
- Što je to linearna diferencijalna jednadžba 2. reda? Kad
kažemo da je homogena, a kad da je nehomogena?
- 2.
- Što su koeficijenti, a što je funkcija smetnje?
- 3.
- Što znate o strukturi skupa svih rješenja?
- 4.
- Što čini skup svih rješenja pripadne homogene jednadžbe?
- 5.
- Koji je kriterij linearne nezavisnosti rješenja homogene
jednadžbe? Što je to determinanta Wronskog?
- 6.
- Kako se rješava linearna diferencijalna jednadžba 2. reda s
konstantnim koeficijentima? Što je karakteristična jednadžba, i
kako dolazimo do nje? Što je karakteristični polinom?
- 7.
- Što je partikularno rješenje? Kako se ono traži u slučaju
posebnog oblika funkcije smetnje? Koji su to posebni oblici?
- 1.
- Lanac duljine
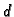 metara leži na vodoravnoj podlozi tako da
metara leži na vodoravnoj podlozi tako da 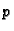 metara visi dolje. Uslijed djelovanja sile teže lanac kliže
dolje. Za koje vrijeme će skliznuti cijeli lanac s podloge, ako
podloga
metara visi dolje. Uslijed djelovanja sile teže lanac kliže
dolje. Za koje vrijeme će skliznuti cijeli lanac s podloge, ako
podloga
- a)
- ne pruža nikakav otpor klizanju,
- b)
- pruža otpor proporcionalan težini
Rješenje. Budući da nije drugačije rečeno, pretpostavlja se da je lanac
homogen, tj. da je gustoća mase lanca 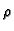 konstanta. Ukupna masa
lanca je
konstanta. Ukupna masa
lanca je
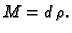 Promjena količine gibanja lanca po jedinici vremena
(derivacija količine gibanja) je prema tome
Promjena količine gibanja lanca po jedinici vremena
(derivacija količine gibanja) je prema tome
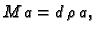 gdje
je
gdje
je 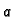 akceleracija lanca. U trenutku
akceleracija lanca. U trenutku 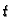 preko podloge visi
preko podloge visi 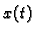 metara lanca. Samo na taj dio lanca djeluje sila teža, pa je sila,
kojom sila teža djeluje na lanac u čas
metara lanca. Samo na taj dio lanca djeluje sila teža, pa je sila,
kojom sila teža djeluje na lanac u čas 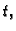 jednaka
jednaka
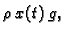 gdje je
gdje je 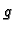 akceleracija sile teže (gravitacija). Prema 2. Newtonovom zakonu, promjena količine gibanja po jedinici vremena
jednaka je sumi svih sila koje djeluju na fizikalni sustav.
akceleracija sile teže (gravitacija). Prema 2. Newtonovom zakonu, promjena količine gibanja po jedinici vremena
jednaka je sumi svih sila koje djeluju na fizikalni sustav.
a) Ako podloga ne pruža otpor, onda je jedina sila koja djeluje sila
teža, pa imamo
s tim da je
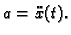 Ako još jednadžbu podijelimo s
Ako još jednadžbu podijelimo s 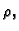 imamo Cauchyjev problem
Ovo je linearna diferencijalna jednadžba 2. reda s konstantnim
koeficijentima, karakteristična jednadžba je
pa je rješenje
Vrijeme potrebno da lanac sklizne s podloge je onaj
imamo Cauchyjev problem
Ovo je linearna diferencijalna jednadžba 2. reda s konstantnim
koeficijentima, karakteristična jednadžba je
pa je rješenje
Vrijeme potrebno da lanac sklizne s podloge je onaj 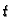 za koji je
za koji je
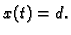 Pozitivno rješenje ove jednadžbe je
Pozitivno rješenje ove jednadžbe je
b) Ako podloga pruža otpor proporcionalan težini (faktor
proporcionalnosti 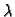 ), onda osim sile teže djeluje još i sila
otpora
), onda osim sile teže djeluje još i sila
otpora
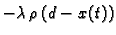 pa u tom slučaju imamo Cauchyjev
problem
pa u tom slučaju imamo Cauchyjev
problem
tj.
Ovo je također linearna diferencijalna
jednadžba 2. reda s konstantnim koeficijentima, i njezino rješenje,
uz početne uvjete je
Sada je rješenje jednadžbe 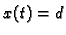
Za izbor parametara
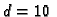 m
m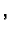
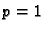 m
m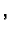
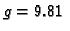 m s
m s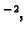
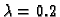 imamo
imamo
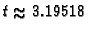
s
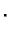
- 2.
- S površine Zemlje bačen je vertikalno uvis projektil mase
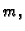 s
početnom brzinom
s
početnom brzinom 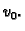 Pretpostavljamo da je otpor zraka proporcionalan
kvadratu brzine (faktor proporcionalnosti
Pretpostavljamo da je otpor zraka proporcionalan
kvadratu brzine (faktor proporcionalnosti 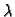 ), i da je akceleracija
sile teže
), i da je akceleracija
sile teže 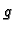 konstanta. Izračunajte do koje će visine stići
projektil.
konstanta. Izračunajte do koje će visine stići
projektil.
Rješenje. Na projektil djeluju sila otpora zraka 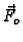 i sila teža
i sila teža
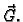
Gibanje se odvija na jednom pravcu, duž tog pravca djeluju i sile, pa
se vektorske veličine mogu zamijeniti skalarnima.
Prilikom uspinjanja obje sile djeluju suprotno od smjera
gibanja. Dakle, ako koordinatni sustav postavimo tako da pozitivni
smjer gibanja znači gibanje u vis, prema 2. Newtonovom zakonu, imamo
gdje je  akceleracija projektila.
akceleracija projektila.
Kako se ovdje ne pojavljuje eksplicitno 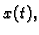 možemo sniziti red
jednadžbe tako da stavimo
možemo sniziti red
jednadžbe tako da stavimo
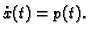 Tada je
Tada je
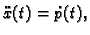 pa jednadžba postaje
pa jednadžba postaje
Ova jednadžba se može riješiti separacijom varijabli. Rješenje je
Neodređenu konstantu računamo iz početnog uvjeta
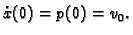 Dobivamo
Dobivamo
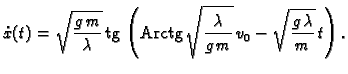 |
(6.40) |
U zadatku se traži maksimalna visina, a ta se dostiže u trenutku kad
je brzina jednaka nuli. Ako, dakle, izjednačimo
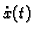 s nulom,
dobivamo vrijeme u kojem se dostigne maksimalna visina
Ako (6.40) još jednom integriramo po
s nulom,
dobivamo vrijeme u kojem se dostigne maksimalna visina
Ako (6.40) još jednom integriramo po 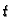 i uvrstimo
početni uvjet
i uvrstimo
početni uvjet 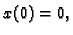 i stavimo
i stavimo
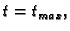 dobivamo
Provjerite da li za
dobivamo
Provjerite da li za
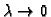 ova
formula prelazi u poznatu formulu
u slučaju vertikalnog hica bez otpora zraka.
ova
formula prelazi u poznatu formulu
u slučaju vertikalnog hica bez otpora zraka.





Next: Linearne jednadžbe višeg reda
Up: Obične diferencijalne jednadžbe
Previous: Linearna diferencijalna jednadžba 1.
Contents
Index
Salih Suljagic
2000-03-11
![]() ,
,
![]() neprekidne funkcije na
neprekidne funkcije na ![]() i
i ![]() , tj.
, tj.
![]() za bar jedan
za bar jedan
![]() Tada jednadžbu
Tada jednadžbu
![]() i
i ![]() , onda je
, onda je
![]() .
Stavimo
.
Stavimo ![]()
![]() onda to
znači da
onda to
znači da ![]() i
i ![]() rješavaju pripadnu homogenu jednadžbu. Tada
rješavaju pripadnu homogenu jednadžbu. Tada
![]() shvatimo kao uređen par
shvatimo kao uređen par ![]() Tada je,
naime,
Tada je,
naime,
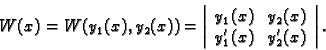
![]() definirana na
definirana na ![]() se zove
Wronskijan ili determinanta Wronskog.
se zove
Wronskijan ili determinanta Wronskog.
![]() se zove fundamentalni sustav rješenja homogene jednadžbe. Iz prethodnog
teorema vidimo da će uređeni par rješenja
se zove fundamentalni sustav rješenja homogene jednadžbe. Iz prethodnog
teorema vidimo da će uređeni par rješenja ![]() biti
fundamentalni sustav rješenja ako i samo ako je
biti
fundamentalni sustav rješenja ako i samo ako je
![]() , a za to je dovoljno provjeriti da je
, a za to je dovoljno provjeriti da je
![]() za
barem jedan
za
barem jedan ![]()
![]() i
i ![]() konstante, onda je taj problem
jednostavno rješiv.
konstante, onda je taj problem
jednostavno rješiv.
![]() jedno dvostruko rješenje
jednadžbe (6.37), onda funkcije
jedno dvostruko rješenje
jednadžbe (6.37), onda funkcije
![]() čine fundamentalni sustav rješenja
jednadžbe (6.36).
čine fundamentalni sustav rješenja
jednadžbe (6.36).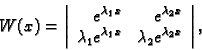
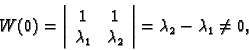
![]() rješenje jednadžbe (6.36).
Stavimo
rješenje jednadžbe (6.36).
Stavimo
![]() .
.
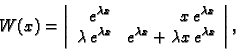
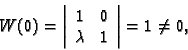
![]() na desnoj strani linearne
diferencijalne jednadžbe
na desnoj strani linearne
diferencijalne jednadžbe
![]() , onda je
, onda je
![]() , onda je
, onda je
![]() jednostruki korijen karakterističnog polinoma, onda
pretpostavljamo
jednostruki korijen karakterističnog polinoma, onda
pretpostavljamo
![]() dvostruki korijen karakterističnog polinoma, onda pretpostavljamo
dvostruki korijen karakterističnog polinoma, onda pretpostavljamo
![]() jednostruki korijen karakterističnog polinoma, onda
jednostruki korijen karakterističnog polinoma, onda
![]() dvostruki korijen karakterističnog polinoma, onda
dvostruki korijen karakterističnog polinoma, onda
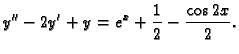
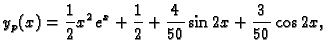
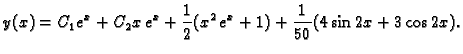
![]() konstanta. Ukupna masa
lanca je
konstanta. Ukupna masa
lanca je
![]() Promjena količine gibanja lanca po jedinici vremena
(derivacija količine gibanja) je prema tome
Promjena količine gibanja lanca po jedinici vremena
(derivacija količine gibanja) je prema tome
![]() gdje
je
gdje
je ![]() akceleracija lanca. U trenutku
akceleracija lanca. U trenutku ![]() preko podloge visi
preko podloge visi ![]() metara lanca. Samo na taj dio lanca djeluje sila teža, pa je sila,
kojom sila teža djeluje na lanac u čas
metara lanca. Samo na taj dio lanca djeluje sila teža, pa je sila,
kojom sila teža djeluje na lanac u čas ![]() jednaka
jednaka
![]() gdje je
gdje je ![]() akceleracija sile teže (gravitacija). Prema 2. Newtonovom zakonu, promjena količine gibanja po jedinici vremena
jednaka je sumi svih sila koje djeluju na fizikalni sustav.
akceleracija sile teže (gravitacija). Prema 2. Newtonovom zakonu, promjena količine gibanja po jedinici vremena
jednaka je sumi svih sila koje djeluju na fizikalni sustav.
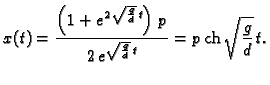
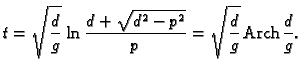
![]() ), onda osim sile teže djeluje još i sila
otpora
), onda osim sile teže djeluje još i sila
otpora
![]() pa u tom slučaju imamo Cauchyjev
problem
pa u tom slučaju imamo Cauchyjev
problem
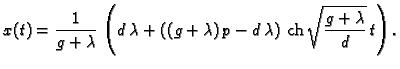
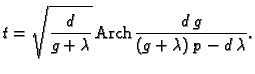
![]() m
m![]()
![]() m
m![]()
![]() m s
m s![]()
![]() imamo
imamo
![]() i sila teža
i sila teža
![]()
![]() možemo sniziti red
jednadžbe tako da stavimo
možemo sniziti red
jednadžbe tako da stavimo
![]() Tada je
Tada je
![]() pa jednadžba postaje
pa jednadžba postaje