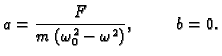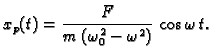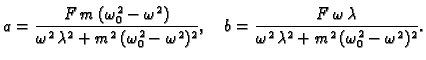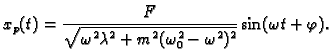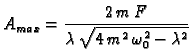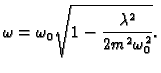Next: Funkcije kompleksne varijable
Up: Obične diferencijalne jednadžbe
Previous: Linearna diferencijalna jednadžba 2.
Contents
Index
Subsections
Pretpostavimo da je
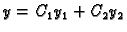 |
(6.41) |
opće rješenje pripadne homogene jednadžbe (6.33). Da dobijemo
opće rješenje nehomogene jednadžbe (6.32) potrebno nam je jedno
partikularno rješenje jednadžbe (6.32). Sljedeći teorem govori o
tome kako se partikularno rješenje jednadžbe (6.32) može dobiti
pomoću (6.41) varirajući konstante 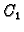 i
i 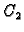 .
.
Teorem 34
Neka je
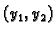
fundamentalni sustav rješenja diferencijalne jednadžbe
i neka su
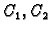
funkcije klase
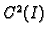
takve da zadovoljavaju sustav
jednadžbi
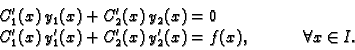 |
(6.42) |
Tada je
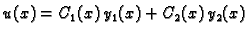 |
(6.43) |
rješenje jednadžbe (
6.32).
Dokaz.
pa je
Dakle 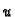 je zaista rješenje jednadžbe (6.32) i time je teorem
dokazan.
je zaista rješenje jednadžbe (6.32) i time je teorem
dokazan.

Da bismo dobili partikularno rješenje (6.43) potrebno je naći funkcije
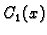 i
i 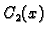 . Budući da su
. Budući da su 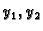 linearno nezavisne, determinanta
matrice sustava (6.42) (Wronskijan) je različita od nule, pa u tom
slučaju imamo jedinstveno rješenje:
linearno nezavisne, determinanta
matrice sustava (6.42) (Wronskijan) je različita od nule, pa u tom
slučaju imamo jedinstveno rješenje:
i odatle
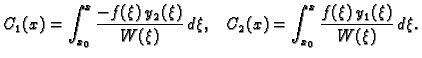 |
(6.44) |
Pomoću formula (6.44), uz poznate 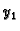 i
i 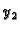 , možemo naći
partikularno rješenje
, možemo naći
partikularno rješenje
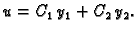
Primjer 6.12
Treba naći opće rješenje jednadžbe
Rješenje. Najprije rješavamo pripadnu homogenu jednadžbu
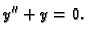 |
(6.45) |
pa je fundamentalni sustav rješenja
Iz Eulerove formule (
7.1) slijedi
pa su
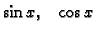 |
(6.46) |
također rješenja jednadžbe (
6.45). Zatim
pa je (
6.46) također fundamentalni sustav rješenja. Tako po
formulama (
6.44) imamo
Odatle, za
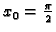
,
Opće rješenje je
tj.
Neka su
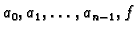 neprekidne realne funkcije definirane na
intervalu
neprekidne realne funkcije definirane na
intervalu 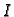 . Jednadžba
. Jednadžba
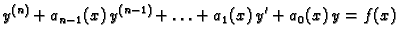 |
(6.47) |
se zove linearna diferencijalna jednadžba n-tog reda.
Cauchyjev problem glasi
i ima jedno i samo jedno rješenje.
Jednadžbu
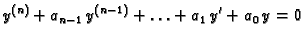 |
(6.48) |
zovemo pripadnom homogenom jednadžbom. Ako je
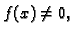 onda jednadžbu zovemo nehomogenom.
Skup
onda jednadžbu zovemo nehomogenom.
Skup 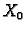 svih rješenja jednadžbe (6.48) je
svih rješenja jednadžbe (6.48) je
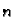 -dimenzionalan vektorski prostor. Proizvoljna baza u
-dimenzionalan vektorski prostor. Proizvoljna baza u 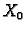 , tj.
proizvoljna uređena
, tj.
proizvoljna uređena 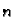 -torka linearno nezavisnih rješenja
jednadžbe (6.48) se zove fundamentalni sustav rješenja. Da funkcije
-torka linearno nezavisnih rješenja
jednadžbe (6.48) se zove fundamentalni sustav rješenja. Da funkcije
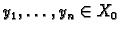 čine fundamentalni sustav rješenja, nužno
je i dovoljno da determinanta Wronskog
bude različita od nule za bar jedan
čine fundamentalni sustav rješenja, nužno
je i dovoljno da determinanta Wronskog
bude različita od nule za bar jedan 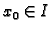 . Ako je
. Ako je
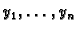 fundamentalni sustav rješenja jednadžbe (6.48), onda je opće
rješenje jednadžbe (6.48)
fundamentalni sustav rješenja jednadžbe (6.48), onda je opće
rješenje jednadžbe (6.48)
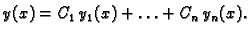 |
(6.49) |
Označimo s 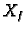 skup svih rješenja jednadžbe (6.47).
Neka je
skup svih rješenja jednadžbe (6.47).
Neka je
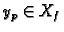 . Tada je
. Tada je
Odatle slijedi da je opće rješenje jednadžbe (6.47) oblika
Partikularno rješenje 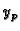 nehomogene jednadžbe možemo dobiti metodom
varijacije konstanti. Pretpostavljamo
nehomogene jednadžbe možemo dobiti metodom
varijacije konstanti. Pretpostavljamo
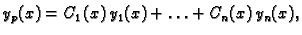 |
(6.50) |
gdje je
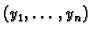 fundamentalni sustav rješenja jednadžbe
(6.48). Ako funkcije
fundamentalni sustav rješenja jednadžbe
(6.48). Ako funkcije
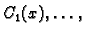
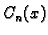 zadovoljavaju
sustav linearnih algebarskih jednadžbi
zadovoljavaju
sustav linearnih algebarskih jednadžbi
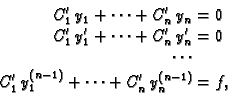 |
(6.51) |
onda 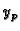 iz (6.50) rješava nehomogenu jednadžbu. Sustav
(6.51) je nehomogen sustav linearnih algebarskih jednadžbi.
Determinanta matrice sustava je determinanta Wronskog, dakle regularna, pa
sustav (6.51) ima jedinstveno rješenje.
iz (6.50) rješava nehomogenu jednadžbu. Sustav
(6.51) je nehomogen sustav linearnih algebarskih jednadžbi.
Determinanta matrice sustava je determinanta Wronskog, dakle regularna, pa
sustav (6.51) ima jedinstveno rješenje.
Ako su u jednadžbi (6.48) koeficijenti
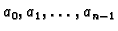 konstante, onda se problem općeg rješenja
homogene jednadžbe svodi na problem nalaženja rješenja algebarske
jednadžbe n-tog stupnja
konstante, onda se problem općeg rješenja
homogene jednadžbe svodi na problem nalaženja rješenja algebarske
jednadžbe n-tog stupnja
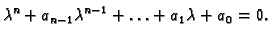 |
(6.52) |
Jednadžba (6.52) se zove karakteristična jednadžba, a
polinom na lijevoj strani karakteristični polinom. Ako su
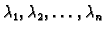 rješenja jednadžbe
(6.52) i međusobno su različiti, onda je opće rješenje
homogene jednadžbe
tj.
rješenja jednadžbe
(6.52) i međusobno su različiti, onda je opće rješenje
homogene jednadžbe
tj.
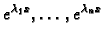 čine fundamentalni sustav
rješenja. Ako je
čine fundamentalni sustav
rješenja. Ako je 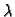 rješenje jednadžbe (6.52)
kratnosti
rješenje jednadžbe (6.52)
kratnosti 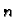 , onda se fundamentalni sustav rješenja dobiva uzimanjem
funkcija
, onda se fundamentalni sustav rješenja dobiva uzimanjem
funkcija
Ako je funkcija  posebnog tipa: polinom, eksponencijalna funkcija i
slično, onda se partikularno rješenje može pretpostaviti u obliku
funkcije istog tipa.
posebnog tipa: polinom, eksponencijalna funkcija i
slično, onda se partikularno rješenje može pretpostaviti u obliku
funkcije istog tipa.
Primjer 6.13
Naći opće rješenje jednadžbe
Rješenje. Korijeni karakterističnog polinoma jesu 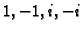 . Prema tome
opće rješenje pripadne homogene jednadžbe je
. Prema tome
opće rješenje pripadne homogene jednadžbe je
Partikularno rješenje treba dakle pretpostaviti u obliku
Nakon uvrštavanja u jednadžbu dobivamo
Prema tome opće rješenje je
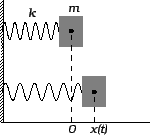
Neka je jedan kraj opruge učvršćen a na drugi kraj je spojeno
tijelo mase 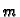 . Pretpostavimo da na ovaj sistem ne djeluje sila
teža, i da se gibanje vrši po pravcu u smjeru opruge. Izvucimo
tijelo iz položaja ravnoteže i pustimo. Ono počinje vršiti neko
gibanje.
. Pretpostavimo da na ovaj sistem ne djeluje sila
teža, i da se gibanje vrši po pravcu u smjeru opruge. Izvucimo
tijelo iz položaja ravnoteže i pustimo. Ono počinje vršiti neko
gibanje.
Iz drugog Newtonovog zakona i Hookeovog zakona dobivamo
jednadžbu gibanja
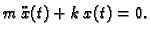 |
(6.53) |
Znati gibanje tijela znači naći iz (6.53) položaj 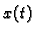 tijela kao
funkciju od
tijela kao
funkciju od 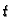 . Podijelimo s
. Podijelimo s 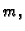 i stavimo
i stavimo
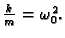 Tako imamo diferencijalnu jednadžbu
To je homogena linearna
diferencijalna jednadžba 2. reda s konstantnim koeficijentima,
korijeni karakterističnog polinoma su
Tako imamo diferencijalnu jednadžbu
To je homogena linearna
diferencijalna jednadžba 2. reda s konstantnim koeficijentima,
korijeni karakterističnog polinoma su
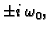 i njezino
opće rješenje je
Zahvaljujući Eulerovoj formuli (7.1)
rješenje možemo prepisati u obliku
gdje je
i njezino
opće rješenje je
Zahvaljujući Eulerovoj formuli (7.1)
rješenje možemo prepisati u obliku
gdje je
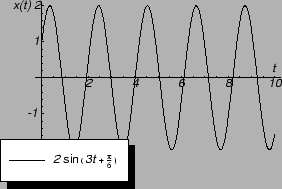
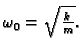 To rješenje se može napisati i ovako
Zbog
postoji
To rješenje se može napisati i ovako
Zbog
postoji
![$ \varphi \in [0,2\pi]$](img3125.gif) takav, da je
Odatle
Dakle, masa se giba periodički s amplitudom
takav, da je
Odatle
Dakle, masa se giba periodički s amplitudom 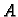 i pomakom u fazi
i pomakom u fazi 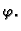 Takvo gibanje se zove slobodno titranje ili slobodne oscilacije,
a
Takvo gibanje se zove slobodno titranje ili slobodne oscilacije,
a 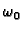 se zove vlastita frekvencija harmonijskog oscilatora.
Uočimo da u izvođenju jednadžbe (6.53) nije bilo važno na
koji smo način pobudili tijelo na gibanje. No ako želimo opisati
gibanje tijela, onda to jeste važno. Tako možemo tijelu u čas
se zove vlastita frekvencija harmonijskog oscilatora.
Uočimo da u izvođenju jednadžbe (6.53) nije bilo važno na
koji smo način pobudili tijelo na gibanje. No ako želimo opisati
gibanje tijela, onda to jeste važno. Tako možemo tijelu u čas 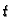 dati neki početni položaj
dati neki početni položaj
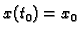 i neku početnu brzinu
i neku početnu brzinu
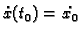 . Akceleraciju
. Akceleraciju
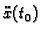 već ne
možemo proizvoljno odrediti jer je jednadžbom (6.53) dana veza
između položaja
već ne
možemo proizvoljno odrediti jer je jednadžbom (6.53) dana veza
između položaja 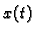 , brzine
, brzine
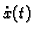 i akceleracije
i akceleracije
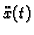 u svakoj točki
u svakoj točki 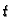 pa i u
pa i u 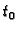 . To odgovara
činjenici da su se u općem rješenju pojavile dvije neodređene konstante
. To odgovara
činjenici da su se u općem rješenju pojavile dvije neodređene konstante
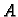 i
i 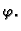
Neka se masa giba u sredstvu u kojem je otpor proporcionalan brzini, na pr.
U tom slučaju diferencijalna jednadžba glasi
odnosno
To je također homogena linearna diferencijalna jednadžba drugog reda s
konstantnim koeficijentima. Rješenja karakteristične jednadžbe su
U slučaju
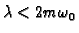 ta rješenja možemo prepisati kao
pa imamo opće rješenje
gdje je
ta rješenja možemo prepisati kao
pa imamo opće rješenje
gdje je
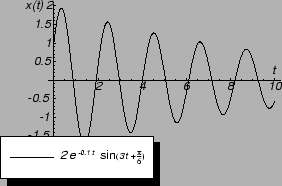
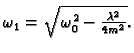 Ovo gibanje se zove prigušeno titranje ili
prigušene oscilacije.
Faktor
Ovo gibanje se zove prigušeno titranje ili
prigušene oscilacije.
Faktor
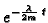 teži prema 0 kad
teži prema 0 kad 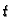 teži u
beskonačnost, pa je on odgovoran za prigušivanje oscilacija. Ako je
teži u
beskonačnost, pa je on odgovoran za prigušivanje oscilacija. Ako je
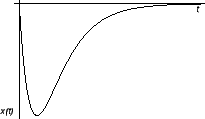
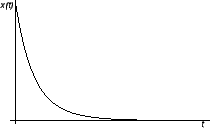
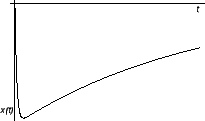
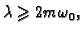 onda su rješenja karakteristične jednadžbe realni brojevi, pa se više ne radi o titranju, već
o aperiodičkom gibanju. Evo nekoliko primjera aperiodičkog gibanja
onda su rješenja karakteristične jednadžbe realni brojevi, pa se više ne radi o titranju, već
o aperiodičkom gibanju. Evo nekoliko primjera aperiodičkog gibanja
Ako na sustav djeluje vanjska periodička sila
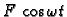 po pravcu
gibanja, onda je diferencijalna jednadžba
po pravcu
gibanja, onda je diferencijalna jednadžba
Partikularno rješenje tražimo u obliku
Promotrimo najprije slučaj kad nema otpora sredstva, tj.
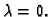 Uvrštavajući
Uvrštavajući 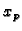 u diferencijalnu jednadžbu dobivamo
Tako je partikularno rješenje
Ovo gibanje se zove prisilno titranje ili prisilne oscilacije harmonijskog oscilatora.
Primjećujemo da, bez obzira na
u diferencijalnu jednadžbu dobivamo
Tako je partikularno rješenje
Ovo gibanje se zove prisilno titranje ili prisilne oscilacije harmonijskog oscilatora.
Primjećujemo da, bez obzira na 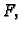 amplituda može biti vrlo velika
ako je
amplituda može biti vrlo velika
ako je
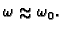 Ta pojava se zove rezonancija.
Titranje sustava duže vrijeme u ovakvim uvjetima može dovesti do zamora
materijala i do rušenja sustava. Ako imamo otpor sredstva, onda
U tom slučaju je partikularno rješenje
Sada se više ne može dogoditi da amplituda raste preko svih granica,
no ako
je
Ta pojava se zove rezonancija.
Titranje sustava duže vrijeme u ovakvim uvjetima može dovesti do zamora
materijala i do rušenja sustava. Ako imamo otpor sredstva, onda
U tom slučaju je partikularno rješenje
Sada se više ne može dogoditi da amplituda raste preko svih granica,
no ako
je 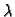 malen (malen otpor sredstva), i
malen (malen otpor sredstva), i
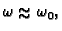 onda
amplituda može biti vrlo velika. Dakle i u tom slučaju imamo mogućnost
pojave rezonancije. Ipak, ekstremalnu vrijednost amplitude dobivamo za
onda
amplituda može biti vrlo velika. Dakle i u tom slučaju imamo mogućnost
pojave rezonancije. Ipak, ekstremalnu vrijednost amplitude dobivamo za
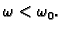 Preciznije, ako amplitudu shvatimo kao funkciju od
Preciznije, ako amplitudu shvatimo kao funkciju od
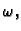 deriviramo i izjednačimo s nulom, dobivamo da amplituda ima
maksimalnu vrijednost
za
deriviramo i izjednačimo s nulom, dobivamo da amplituda ima
maksimalnu vrijednost
za
- 1.
- Kako se može naći partikularno rješenje općenito. Objasnite
metodu varijacije konstanti.
- 2.
- Napišite linearnu diferencijalnu jednadžbu
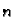 -tog
reda. Objasnite u vezi s njom pojmove: koeficijenti, funkcija smetnje,
struktura skupa svih rješenja, vektorski prostor skupa svih rješenja
pripadne homogene jednadžbe, karakteristična jednadžba, metoda
varijacije konstanti.
-tog
reda. Objasnite u vezi s njom pojmove: koeficijenti, funkcija smetnje,
struktura skupa svih rješenja, vektorski prostor skupa svih rješenja
pripadne homogene jednadžbe, karakteristična jednadžba, metoda
varijacije konstanti.
- 3.
- Što znate o harmonijskom oscilatoru? Objasnite pojavu rezonancije.





Next: Funkcije kompleksne varijable
Up: Obične diferencijalne jednadžbe
Previous: Linearna diferencijalna jednadžba 2.
Contents
Index
Salih Suljagic
2000-03-11
![]() i
i ![]() . Budući da su
. Budući da su ![]() linearno nezavisne, determinanta
matrice sustava (6.42) (Wronskijan) je različita od nule, pa u tom
slučaju imamo jedinstveno rješenje:
linearno nezavisne, determinanta
matrice sustava (6.42) (Wronskijan) je različita od nule, pa u tom
slučaju imamo jedinstveno rješenje:
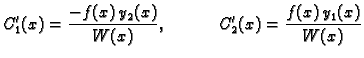
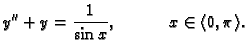
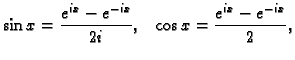
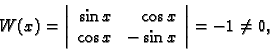
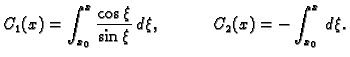
![]() neprekidne realne funkcije definirane na
intervalu
neprekidne realne funkcije definirane na
intervalu ![]() . Jednadžba
. Jednadžba
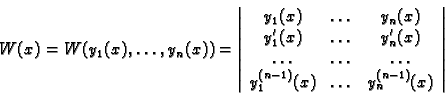
![]() skup svih rješenja jednadžbe (6.47).
Neka je
skup svih rješenja jednadžbe (6.47).
Neka je
![]() . Tada je
. Tada je
![]() konstante, onda se problem općeg rješenja
homogene jednadžbe svodi na problem nalaženja rješenja algebarske
jednadžbe n-tog stupnja
konstante, onda se problem općeg rješenja
homogene jednadžbe svodi na problem nalaženja rješenja algebarske
jednadžbe n-tog stupnja
![]() posebnog tipa: polinom, eksponencijalna funkcija i
slično, onda se partikularno rješenje može pretpostaviti u obliku
funkcije istog tipa.
posebnog tipa: polinom, eksponencijalna funkcija i
slično, onda se partikularno rješenje može pretpostaviti u obliku
funkcije istog tipa.
![]() . Prema tome
opće rješenje pripadne homogene jednadžbe je
. Prema tome
opće rješenje pripadne homogene jednadžbe je
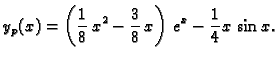
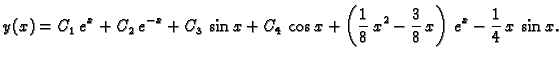
![]() . Pretpostavimo da na ovaj sistem ne djeluje sila
teža, i da se gibanje vrši po pravcu u smjeru opruge. Izvucimo
tijelo iz položaja ravnoteže i pustimo. Ono počinje vršiti neko
gibanje.
. Pretpostavimo da na ovaj sistem ne djeluje sila
teža, i da se gibanje vrši po pravcu u smjeru opruge. Izvucimo
tijelo iz položaja ravnoteže i pustimo. Ono počinje vršiti neko
gibanje.
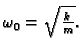 To rješenje se može napisati i ovako
To rješenje se može napisati i ovako
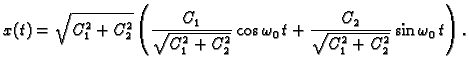
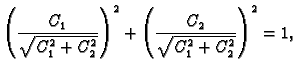
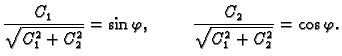
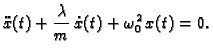
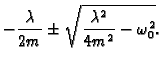
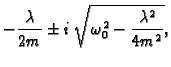
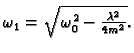 Ovo gibanje se zove prigušeno titranje ili
prigušene oscilacije.
Ovo gibanje se zove prigušeno titranje ili
prigušene oscilacije.
![]() po pravcu
gibanja, onda je diferencijalna jednadžba
po pravcu
gibanja, onda je diferencijalna jednadžba