Next: Plošni integrali
Up: Polja
Previous: Skalarna i vektorska polja.
Contents
Index
Subsections
Definicija 40
Neka je
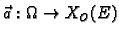
vektorsko polje klase
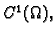
neka je dan Kartezijev pravokutni koordinatni sustav
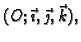
i neka je
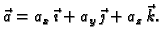
Skalarno polje
se zove
divergencija vektorskog polja 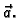
Definicija 41
Neka je
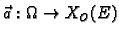
vektorsko polje klase
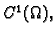
neka je dan
desni Kartezijev pravokutni koordinatni
sustav
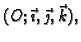
i neka je
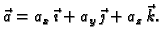
Vektorsko polje
se zove
rotacija vektorskog polja 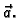
Iz definicije se vidi da divergenciju možemo zapisati pomoću
diferencijalnog operatora 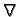 na način
na način
a rotaciju na način
Kako je 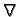 diferencijalni operator, njegovo djelovanje ima
svojstva derivacije.
diferencijalni operator, njegovo djelovanje ima
svojstva derivacije.
- 1.
- Ako su
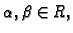 i
i
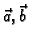 vektorska
polja, onda vrijedi
vektorska
polja, onda vrijedi
- 2.
- Ako je
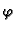 skalarno polje,
skalarno polje,  vektorsko polje,
onda vrijedi
(Ovdje smo podcrtali veličine na koje nabla ne djeluje.)
vektorsko polje,
onda vrijedi
(Ovdje smo podcrtali veličine na koje nabla ne djeluje.)
- 3.
- Ako su
 i
i 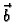 vektorska polja, onda vrijedi
vektorska polja, onda vrijedi
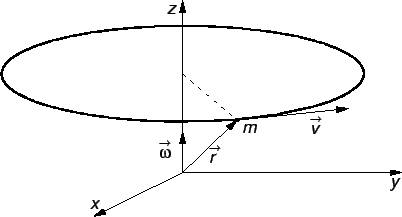
Primjer 4.11
Neka materijalna točka rotira jednoliko oko osi
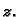
Njezina trajektorija je dana kao skup vrhova radijvektora
Odatle je
Brzina je
pa je tako kutna brzina
Primjer 4.12
Polje pomaka prilikom torzije cilindra je
Duljina vektora
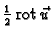
daje kut zakreta, dok
njegov smjer pokazuje, pravilom desne ruke, smjer zakreta.
Primjer 4.13
Naći divergenciju vektorskog polja
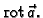
Rješenje. Primijenimo li formalizam iz vektorske algebre, imamo
jer su dva retka u ovoj 'determinanti' jednaka.
Definicija 42
Neka je
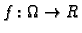
skalarno polje klase
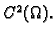
Skalarno polje
zovemo
Laplaceom skalarnog polja 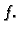
Jednadžba
se zove
Laplaceova jednadžba, a njezina rješenja zovemo
harmonijskim funkcijama.
Primjer 4.14
Neka je
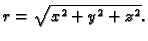
Naći
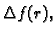
gdje je

funkcija dvaput neprekidno derivabilna.
Rješenje. Koristeći primjer 4.10, imamo
Tako je
Specijalno, ako je
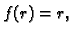
imamo
a u slučaju
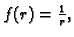
imamo
Tako vidimo da je funkcija
harmonijska.
Da li je funkcija
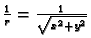 harmonijska?
harmonijska?
Definicija 43
Vektorsko polje

zovemo
potencijalnim (konzervativnim),
ako postoji skalarno polje
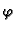
takvo, da je
U tom slučaju skalarno polje
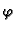
zovemo
potencijalom
vektorskog polja
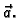
Primjer 4.15
U primjerima
4.4 i
4.9 smo
imali upravo takav slučaj. Vektorsko polje
se zove električno polje točkastog naboja, i ono je kao što smo
vidjeli negativni gradijent skalarnog polja
Predznak 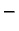 nije bitan, jer je
nije bitan, jer je
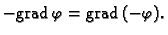 On se stavlja zbog fizikalnih razloga.
On se stavlja zbog fizikalnih razloga.
Kriterij za odlučivanje o tome da li je vektorsko polje potencijalno
dan je sljedećim teoremom.
Teorem 19
Neka je

konveksno područje. Neka je
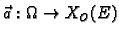
vektorsko polje neprekidno na području
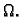
Polje

je potencijalno ako i samo ako je
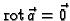
.
Dokaz. U jednom smjeru dokaz je
jednostavan. Ako je vektorsko polje  potencijalno, onda je
potencijalno, onda je
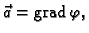 pa je
pa je
jer su dva retka u 'determinanti' jednaka.

U potencijalnom polju krivuljni integral 2. vrste (rad sile na putu
po krivulji) ima jedno osobito svojstvo, koje se iskazuje sljedećim
teoremom.
Teorem 20
Neka je

konveksno područje. Neka je
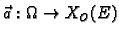
vektorsko polje
neprekidno na području
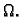
Polje

je potencijalno
ako i samo ako krivuljni integral 2. vrste polja

ne ovisi
o putu, već samo o krajnjim točkama.
Dokaz. 1. Dokažimo najprije da
potencijalnost polja povlači nezavisnost integrala o
putu. Pretpostavimo, dakle, da je  potencijalno polje. To
znači da postoji skalarno polje
potencijalno polje. To
znači da postoji skalarno polje 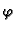 takvo da je
takvo da je
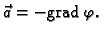 Neka je
Neka je  krivulja u
krivulja u 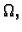 i
neka je njezina parametrizacija
i
neka je njezina parametrizacija
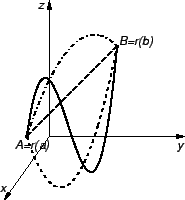
2. Dokažimo obrat, tj. da nezavisnost krivuljnog integrala
polja  o
putu iz točke
o
putu iz točke
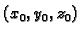 u točku
u točku 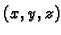 povlači
potencijalnost vektorskog polja
povlači
potencijalnost vektorskog polja 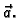 Budući da krivuljni
integral ne ovisi o putu, možemo pisati
Tvrdimo da je
U tu svrhu izračunajmo
Budući da krivuljni
integral ne ovisi o putu, možemo pisati
Tvrdimo da je
U tu svrhu izračunajmo
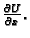 Put od točke
Put od točke 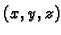 do točke
do točke
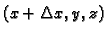 parametriziramo
tako da uzmemo
Tada je
parametriziramo
tako da uzmemo
Tada je
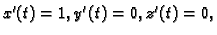 pa imamo (v. 3.3.3)
Po teoremu srednje vrijednosti za integrale, postoji
pa imamo (v. 3.3.3)
Po teoremu srednje vrijednosti za integrale, postoji
![$ \tau\in [x,x+\Delta{}x]$](img2321.gif) takav da je
Iz neprekidnosti vektorskog polja
takav da je
Iz neprekidnosti vektorskog polja  slijedi da je
slijedi da je 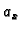 neprekidna funkcija, pa je limes jednak vrijednosti funkcije, dakle
Na istovjetan način se dokazuje da
neprekidna funkcija, pa je limes jednak vrijednosti funkcije, dakle
Na istovjetan način se dokazuje da

U potencijalnom (konzervativnom) polju sile imamo potencijal. Ploha na
kojoj potencijal u svakoj točki ima istu vrijednost zove se
ekvipotencijalna ploha. Na temelju formule iz prvog dijela dokaza
teorema 20 možemo zaključiti da rad sile ne ovisi
o putu, pa čak niti o početnoj i završnoj točki, već samo o
početnoj i završnoj ekvipotencijalnoj plohi. Tako gibanje po
ekvipotencijalnoj plohi ne zahtijeva nikakav utrošak rada (gibanje
satelita u orbitama oko Zemlje).
Pogledajmo sada kako se može izračunati potencijal, ako je zadano
potencijalno polje.
Neka je
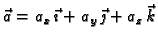 potencijalno polje. Postoji, dakle, skalarno polje
potencijalno polje. Postoji, dakle, skalarno polje 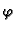 takvo, da je
takvo, da je
Odatle
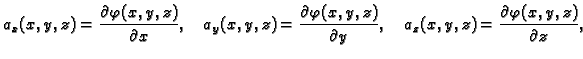 |
(4.1) |
i prema tome
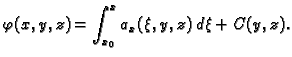 |
(4.2) |
Da odredimo 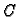 derivirajmo ovu formulu po
derivirajmo ovu formulu po 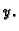 Iz
Iz
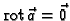 (v. teorem 19) slijedi
Tako je
To znači, zbog (4.1)
Odatle
Sada na sličan način odredimo
(v. teorem 19) slijedi
Tako je
To znači, zbog (4.1)
Odatle
Sada na sličan način odredimo 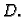 Iz
Iz
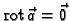 slijedi
Tako je
S druge strane, iz formule (4.2) slijedi
Odatle
i prema tome
Tako je
gdje je
slijedi
Tako je
S druge strane, iz formule (4.2) slijedi
Odatle
i prema tome
Tako je
gdje je 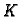 proizvoljna konstanta. Kad sve to skupimo zajedno, dobivamo
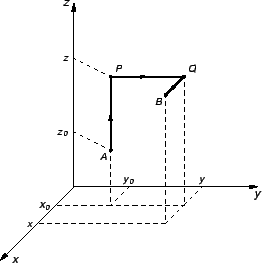
Treći integral predstavlja krivuljni integral po spojnici od točke
proizvoljna konstanta. Kad sve to skupimo zajedno, dobivamo
Treći integral predstavlja krivuljni integral po spojnici od točke
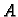 do točke
do točke 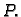 Drugi integral je krivuljni integral po spojnici od
točke
Drugi integral je krivuljni integral po spojnici od
točke 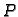 do točke
do točke 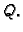 Konačno prvi integral je krivuljni integral
po spojnici od točke
Konačno prvi integral je krivuljni integral
po spojnici od točke 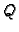 do točke
do točke 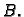
Primjer 4.16
Nađimo potencijal gravitacijskog polja.
Rješenje. Gravitacijsko polje je dano formulom
Tako je
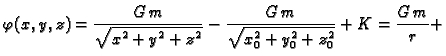
konst.
Definicija 44
Vektorsko polje

zovemo
solenoidalnim, ako postoji
vektorsko polje
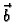
takvo, da je
Teorem 21
Neka je

konveksno područje. Neka je
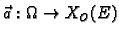
vektorsko polje neprekidno na području
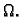
Polje

je solenoidalno ako i samo ako je
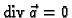
.
Dokaz. U jednom smjeru je dokaz
jednostavan. Ako je vektorsko polje  solenoidalno, onda je
solenoidalno, onda je
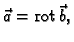 pa je prema primjeru 4.13
pa je prema primjeru 4.13

Primjer 4.17
Vektorsko polje pomaka u primjeru
4.8 je
solenoidalno.
Rješenje. Doista,
Svako vektorsko polje dvaput neprekidno derivabilno se može
rastaviti na zbroj potencijalnog i solenoidalnog polja.
Neka je  takvo polje. Stavimo
takvo polje. Stavimo
gdje za sada skalarno polje 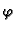 nije određeno.
Sada
nije određeno.
Sada 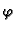 odredimo iz uvjeta
Budući da je
odredimo iz uvjeta
Budući da je
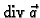 neprekidna funkcija, ova jednadžba ima
rješenja, i to njih beskonačno mnogo. Tako je
neprekidna funkcija, ova jednadžba ima
rješenja, i to njih beskonačno mnogo. Tako je
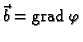 potencijalno, a
potencijalno, a 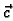 solenoidalno polje.
solenoidalno polje.
- 1.
- Definirajte divergenciju i rotaciju vektorskog polja. Koja
svojstva imaju?
- 2.
- Kako se definira Laplace? Što su to harmonijske funkcije?
- 3.
- Kada neko vektorsko polje zovemo potencijalnim? Što je
potencijal? Da li je jednoznačno određen?
- 4.
- Koje osbito svojstvo ima potencijalno polje u odnosu na
integriranje po krivuljama? Koja je fizikalna posljedica tog svojstva?
- 5.
- Navedite kriterij za potencijalnost vektorskog polja. Dokažite
nužnost kriterija.
- 6.
- Po kojoj formuli se računa potencijal? Objasnite zašto.
- 7.
- Kada neko vektorsko polje zovemo solenoidalnim? Koji je kriterij
za solenoidalnost?
- 8.
- Kako se proizvoljno vektorsko polje može rastaviti na
potencijalno i solenoidalno? Objasnite.
- 1.
- Uvjerite se da je polje
potencijalno, i nađite potencijal.
Rješenje. Parcijalne derivacije su redom
Odatle
i prema tome polje je potencijalno. Potencijal je, do na konstantu,
- 2.
- Rastaviti vektorsko polje
na potencijalno i solenoidalno polje.
Rješenje.
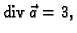 pa se potencijalno polje
pa se potencijalno polje 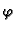 određuje
iz zahtjeva
određuje
iz zahtjeva
Ova jednadžba ima mnogo rješenja. Jedno od njih je na pr.
Tada je solenoidalno polje





Next: Plošni integrali
Up: Polja
Previous: Skalarna i vektorska polja.
Contents
Index
Salih Suljagic
2000-03-11
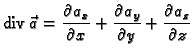
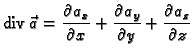
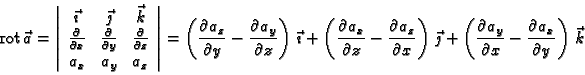
![]() na način
na način
![]() diferencijalni operator, njegovo djelovanje ima
svojstva derivacije.
diferencijalni operator, njegovo djelovanje ima
svojstva derivacije.
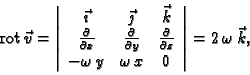
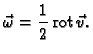
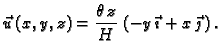
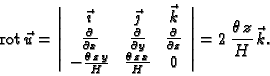
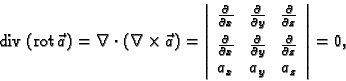
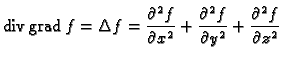
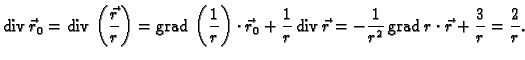
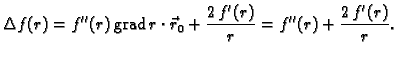
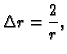
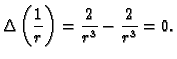
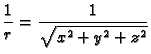
![]() harmonijska?
harmonijska?
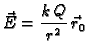
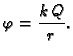
![]() nije bitan, jer je
nije bitan, jer je
![]() On se stavlja zbog fizikalnih razloga.
On se stavlja zbog fizikalnih razloga.
![]() potencijalno, onda je
potencijalno, onda je
![]() pa je
pa je
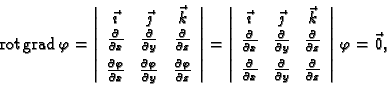
![]() potencijalno polje. To
znači da postoji skalarno polje
potencijalno polje. To
znači da postoji skalarno polje ![]() takvo da je
takvo da je
![]() Neka je
Neka je ![]() krivulja u
krivulja u ![]() i
neka je njezina parametrizacija
i
neka je njezina parametrizacija
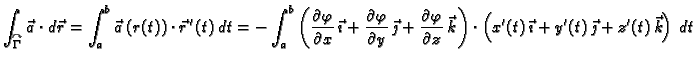
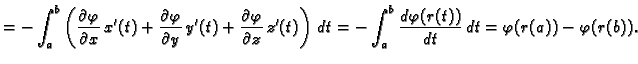
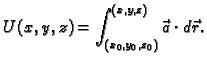
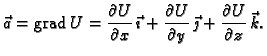
![$\displaystyle \frac{\partial U}{\partial x} = \lim_{\Delta{}x\rightarrow{}0}
\f...
...{a}\cdot d\vec{r} - \int_{(x_0,y_0,z_0)}^{(x,y,z)} \vec{a}\cdot
d\vec{r}\right]$](img2315.gif)
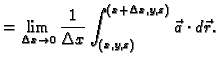
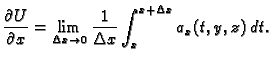
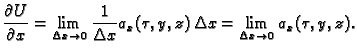
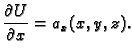
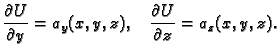
![]() potencijalno polje. Postoji, dakle, skalarno polje
potencijalno polje. Postoji, dakle, skalarno polje ![]() takvo, da je
takvo, da je
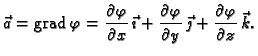
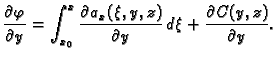
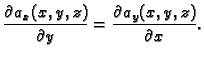
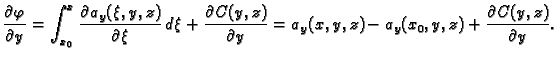
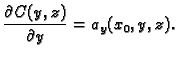
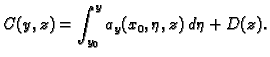
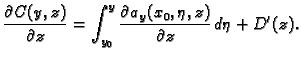
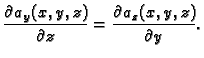
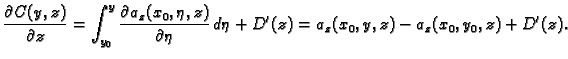
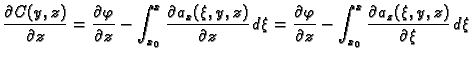
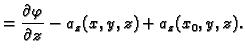
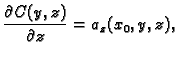
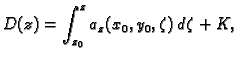
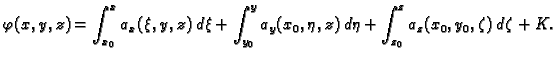
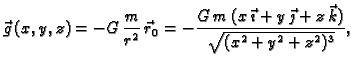
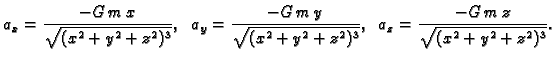
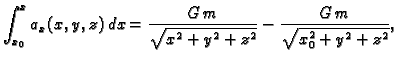
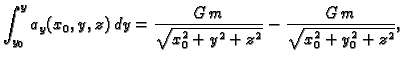
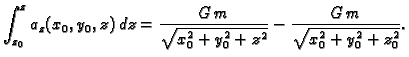
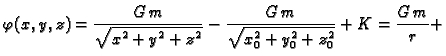 konst.
konst.
![]() solenoidalno, onda je
solenoidalno, onda je
![]() pa je prema primjeru 4.13
pa je prema primjeru 4.13
![]() takvo polje. Stavimo
takvo polje. Stavimo
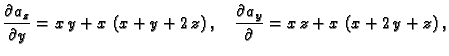
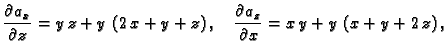
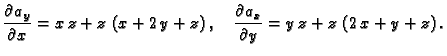
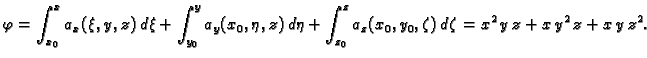
![]() pa se potencijalno polje
pa se potencijalno polje ![]() određuje
iz zahtjeva
određuje
iz zahtjeva