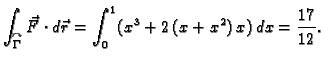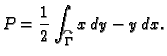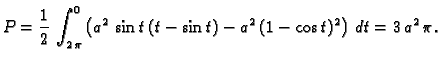Next: Krivulje u prostoru
Up: Krivulje i krivuljni integrali
Previous: Krivuljni integral 1. vrste
Contents
Index
Subsections
Neka je  glatka krivulja u prostoru (Jordanov luk). U svakoj
točki krivulje postoji tangenta.
Orijentirati
krivulju
glatka krivulja u prostoru (Jordanov luk). U svakoj
točki krivulje postoji tangenta.
Orijentirati
krivulju  znači u svakoj točki krivulje odabrati jedan od
dva moguća jedinična vektora u smjeru tangente.
znači u svakoj točki krivulje odabrati jedan od
dva moguća jedinična vektora u smjeru tangente.
Ima beskonačno
mnogo načina da se krivulja orijentira. Međutim, ako želimo da to
pridruživanje bude neprekidno, onda imamo samo dva načina, i to tako
da jedinični vektori tangente pokazuju gibanje po krivulji u
određenom smjeru, na pr. od  do
do 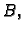 ili u njemu suprotnom
smjeru, od
ili u njemu suprotnom
smjeru, od 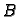 do
do 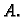
Parametrizacija
![$ ([a,b],\vec{r}\,)$](img1659.gif) nudi jednu takvu orijentaciju, jer je
parametrizacijom potpuno zadan vektor
nudi jednu takvu orijentaciju, jer je
parametrizacijom potpuno zadan vektor
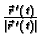 koji je
upravo jedinični vektor tangente na krivulju
koji je
upravo jedinični vektor tangente na krivulju  u točki
u točki
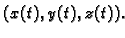 U daljnjem ćemo pretpostavljati da su
parametrizacija i orijentacija u skladu.
U daljnjem ćemo pretpostavljati da su
parametrizacija i orijentacija u skladu.
Primjer 3.12
Neka je

jedinična kružnica sa središtem u
ishodištu. Parametrizacija
daje jednu orijentaciju, dok
daje suprotnu orijentaciju.
Ako je glatka krivulja  zatvorena i nalazi se u ravnini, onda
kažemo da je pozitivno orijentirana, ako vektori tangente nalažu
gibanje po krivulji protivno kretanju kazaljke na satu. U suprotnom,
kažemo da je krivulja negativno orijentirana.
zatvorena i nalazi se u ravnini, onda
kažemo da je pozitivno orijentirana, ako vektori tangente nalažu
gibanje po krivulji protivno kretanju kazaljke na satu. U suprotnom,
kažemo da je krivulja negativno orijentirana.
Orijentiranu krivulju  ćemo zapisivati kao
ćemo zapisivati kao
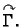
Neka je
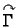 glatka orijentirana krivulja
u prostoru. Neka je
glatka orijentirana krivulja
u prostoru. Neka je 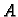 početna, a
početna, a 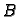 završna točka krivulje. Neka
se krivulja nalazi u polju neke sile. To znači da u svakoj točki
završna točka krivulje. Neka
se krivulja nalazi u polju neke sile. To znači da u svakoj točki 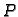 krivulje djeluje akceleracija
krivulje djeluje akceleracija
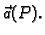 Da bi materijalna točka
mase
Da bi materijalna točka
mase 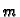 po krivulji prešla put od početne točke
po krivulji prešla put od početne točke 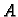 do završne
točke
do završne
točke 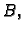 potrebno je izvršiti neki rad. Interesira nas koliko
iznosi potrebni rad. Da bismo ga izračunali, podijelimo krivulju
točkama
potrebno je izvršiti neki rad. Interesira nas koliko
iznosi potrebni rad. Da bismo ga izračunali, podijelimo krivulju
točkama
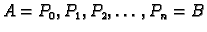 na manje dijelove. Rad sile
duž orijentiranog luka
na manje dijelove. Rad sile
duž orijentiranog luka
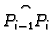 je približno
je približno
gdje je 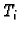 proizvoljno izabrana točka na luku
proizvoljno izabrana točka na luku
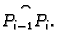 Ukupni rad je približno jednak
Očekujemo da će ova približna vrijednost biti to bliže pravoj
vrijednosti rada, što finiju podjelu krivulje napravimo.
Ukupni rad je približno jednak
Očekujemo da će ova približna vrijednost biti to bliže pravoj
vrijednosti rada, što finiju podjelu krivulje napravimo.
Neka je  područje u
područje u 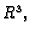 i
i
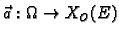 vektorska funkcija. Neka je
vektorska funkcija. Neka je
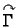 glatka orijentirana krivulja u
glatka orijentirana krivulja u
 tako da je
tako da je 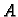 početna, a
početna, a 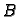 završna točka.
Podijelimo krivulju na manje dijelove točkama
završna točka.
Podijelimo krivulju na manje dijelove točkama
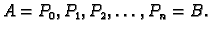 Na dijelu krivulje
Na dijelu krivulje
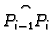 izaberimo proizvoljno točku
izaberimo proizvoljno točku 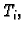 i to za svaki
i to za svaki
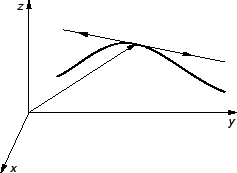
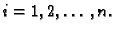 (v. sliku 3.3.1.) Uočimo sljedeću sumu
(v. sliku 3.3.1.) Uočimo sljedeću sumu
Broj 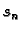 ovisi o
broju
ovisi o
broju 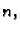 i o točkama
i o točkama 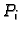 i
i 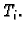 Pustimo da
Pustimo da
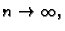 i pri tom neka su podjele takve da duljina
najvećeg dijela krivulje teži k
i pri tom neka su podjele takve da duljina
najvećeg dijela krivulje teži k 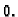 Ako uz te uvjete
Ako uz te uvjete 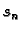 teži
prema nekom broju
teži
prema nekom broju 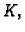 onda se taj broj zove krivuljni integral 2.
vrste vektorske funkcije
onda se taj broj zove krivuljni integral 2.
vrste vektorske funkcije  po krivulji
po krivulji
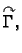 i piše se
i piše se
Svojstva krivuljnog integrala 2. vrste
- 1.
-
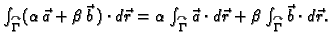
- 2.
-
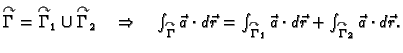
- 3.
-
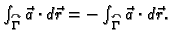
Neka je
 glatka orijentirana
krivulja u prostoru, i neka je njezina parametrizacija
glatka orijentirana
krivulja u prostoru, i neka je njezina parametrizacija
![$ ([a,b],\vec{r}\,),$](img1786.gif) gdje je
gdje je
u skladu s orijentacijom. Neka je na
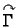 zadana vektorska funkcija
zadana vektorska funkcija
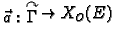 takva da
postoji
takva da
postoji
Podijelimo segment ![$ [a,b]$](img986.gif) na podsegmente
na podsegmente
Tako dobivamo točke na krivulji
Izaberimo
![$ \xi_i\in [t_{i-1},t_i]$](img1792.gif) proizvoljno, i neka je
proizvoljno, i neka je
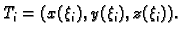 Tada je
Prema Lagrangeovom teoremu
srednje vrijednosti, postoje
Tada je
Prema Lagrangeovom teoremu
srednje vrijednosti, postoje
![$ \rho_i,
\sigma_i, \tau_i\in [t_{i-1},t_i]$](img1796.gif) takvi da je
za svaki
takvi da je
za svaki
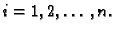 Slijedi
Ovo je integralna suma za funkciju
Prema tome krivuljni
integral 2. vrste se računa po formuli
Slijedi
Ovo je integralna suma za funkciju
Prema tome krivuljni
integral 2. vrste se računa po formuli
Krivuljni integral 2. vrste se može zapisati i na sljedeći način
To dolazi odatle što se u formuli za 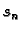 može pisati
može pisati
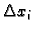 umjesto
umjesto
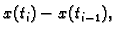
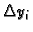 umjesto
umjesto
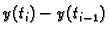 i
i
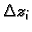 umjesto
umjesto
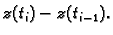
Primjer 3.13
Izračunati
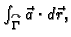
ako je
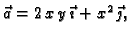
a krivulja
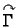
je
- a)
- dio pravca
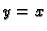 od točke
od točke 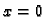 do
do 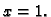
- b)
- dio parabole
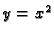 od točke
od točke 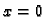 do
do 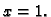
Rješenje. a) Za parametar možemo uzeti 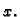 Tako je
Tako je
b) Također za parametar možemo uzeti 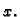
Primjer 3.14
Izračunati rad sile
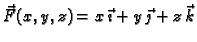
duž prvog zavoja helikoide
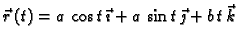
od točke
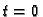
do
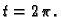
Rješenje.
Vektor
je jedinični vektor tangente, dok je
Tako imamo
Zadnji integral je krivuljni integral 1. vrste skalarne funkcije
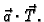 Krivuljni integral 1. vrste ne ovisi o
orijentaciji. To se vidi iz formule za računanje
iz koje je jasno da smjer vektora tangente nije
bitan. S druge strane krivuljni integral 2. vrste ovisi o
orijentaciji, kao što se tvrdi u 3. svojstvu 3.3.2.
Odgovor na pitanje: kako se mogu povezati integrali od kojih jedan
mijenja znak prilikom promijene orijentacije, a drugi ne, leži u
činjenici da se u podintegralnoj funkciji krivuljnog integrala 1.
vrste pojavio vektor
Krivuljni integral 1. vrste ne ovisi o
orijentaciji. To se vidi iz formule za računanje
iz koje je jasno da smjer vektora tangente nije
bitan. S druge strane krivuljni integral 2. vrste ovisi o
orijentaciji, kao što se tvrdi u 3. svojstvu 3.3.2.
Odgovor na pitanje: kako se mogu povezati integrali od kojih jedan
mijenja znak prilikom promijene orijentacije, a drugi ne, leži u
činjenici da se u podintegralnoj funkciji krivuljnog integrala 1.
vrste pojavio vektor 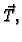 koji prilikom promjene orijentacije
mijenja znak.
koji prilikom promjene orijentacije
mijenja znak.
Jednostruko povezano područje  u
u 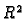 je područje koje ima svojstvo da se svaka zatvorena krivulja u
je područje koje ima svojstvo da se svaka zatvorena krivulja u
 može bez prekidanja stegnuti na točku ne izlazeći iz
može bez prekidanja stegnuti na točku ne izlazeći iz
 Na slici 2.3 imamo primjer područja koje
je jednostruko povezano. S druge strane na slici 1.5
imamo primjer područja koje nije jednostruko povezano. Ako opišemo
zatvorenu krivulju u području oko šupljine, onda nije moguće
stegnuti tu krivulju bez kidanja na točku ne izlazeći iz područja.
Takvo područje se zove višestruko povezano
područje.
Na slici 2.3 imamo primjer područja koje
je jednostruko povezano. S druge strane na slici 1.5
imamo primjer područja koje nije jednostruko povezano. Ako opišemo
zatvorenu krivulju u području oko šupljine, onda nije moguće
stegnuti tu krivulju bez kidanja na točku ne izlazeći iz područja.
Takvo područje se zove višestruko povezano
područje.
Teorem 18
(Greenov teorem)
Neka je

jednostruko povezano područje u
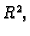
i neka su
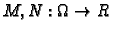
funkcije klase
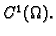
Neka je u

zadana jednostavna glatka zatvorena pozitivno orijentirana
krivulja
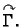
Neka je

područje
u

koje omeđuje
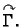
Tada
vrijedi sljedeća formula.
Dokaz. Izračunajmo najprije
Slika 3.3:
Greenov teorem.
|
|
Krivulju  možemo shvatiti kao uniju od dvije krivulje
možemo shvatiti kao uniju od dvije krivulje
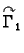 parametrizirane kao
parametrizirane kao
![$ (x,f_1(x)),\;x\in [a,b],$](img1926.gif) i
i
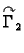 parametrizirane kao
parametrizirane kao
![$ (x,f_2(x)),\;x\in [a,b].$](img1928.gif) Tako je
Na sličan način možemo izračunati da je
shvaćajući
Tako je
Na sličan način možemo izračunati da je
shvaćajući  kao uniju od
kao uniju od
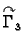 parametrizirane kao
parametrizirane kao
![$ (g_1(y),y),\;y\in [c,d],$](img1933.gif) i
i
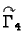 parametrizirane kao
parametrizirane kao
![$ (g_2(y),y),\;y\in [c,d].$](img1935.gif) Sada, međutim, idući od
Sada, međutim, idući od 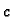 do
do 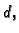 predznak
predznak 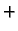 ima krivuljni integral po
ima krivuljni integral po
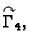 a
a 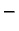 onaj po
onaj po
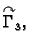 pa nema potrebe mijenjati granice.
pa nema potrebe mijenjati granice.

Formula u ovom teoremu se zove Greenova
formula. Kako se iz
formule vidi, tu se radi o vezi između krivuljnog integrala 2. vrste
po zatvorenoj pozitivno orijentiranoj krivulji u ravnini i dvostrukog
integrala po području omeđenom tom krivuljom.
Primjer 3.15
Provjerimo Greenovu formulu na primjeru funkcija
i središnje kružnice radiusa
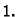
Rješenje.
S druge strane, uz parametrizaciju kružnice
![$ (\cos t,\sin t),\;t\in
[0,2\,\pi],$](img1943.gif)
imamo
Dakle, Greenova formula ne vrijedi. Uzrok tome je što uvjeti
Greenovog teorema nisu bili ispunjeni. Funkcije
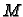
i
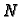
nisu klase
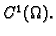
Dapače, u točki
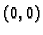
nisu uopće definirane.
Greenov teorem ima važnu ulogu u teorijskim razmatranjima u primjeni
matematike. No, i u praktičnom računanju može se koristiti, posebno
kad prilikom računanja krivuljnog integrala vodi na jednostavan
dvostruki integral.
Primjer 3.16
Izračunati
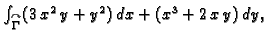
gdje je

pozitivno orijentirana kružnica
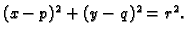
Rješenje. Funkcije 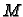 i
i 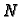 zadovoljavaju uvjete Greenovog
teorema,
zadovoljavaju uvjete Greenovog
teorema,
pa je
Pomoću krivuljnog integrala 2. vrste po pozitivno orijentiranom rubu
lika 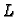 u ravnini može se, zahvaljujući Greenovoj formuli, naći
površina lika
u ravnini može se, zahvaljujući Greenovoj formuli, naći
površina lika 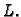 Površina lika
Površina lika 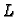 je
je
Neka je
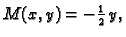 a
a
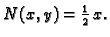 pa je
gdje je
pa je
gdje je
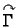 pozitivno orijentiran rub
lika
pozitivno orijentiran rub
lika  Tako imamo formulu za površinu lika
Tako imamo formulu za površinu lika
Primjer 3.17
Naći površinu lika omeđenog elipsom
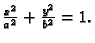
Rješenje. Parametrizacija elipse je
pa je
- 1.
- Što znači orijentirati glatku krivulju? Zašto ima smisla
govoriti o orijentaciji samo kod glatkih krivulja?
- 2.
- Definirajte krivuljni integral 2. vrste. Koji problem rješava?
Kako se računa? Koja svojstva ima?
- 3.
- Koja je veza između krivuljnih integrala 1. i 2. vrste?
- 4.
- Kako glasi Greenov teorem? Dokažite ga.
- 5.
- Kako se može računati površina ravninskog lika pomoću
krivuljnog integrala?
- 1.
- Neka je
 jednostruko povezano područje, i neka je
jednostruko povezano područje, i neka je
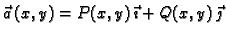 vektorska
funkcija klase
vektorska
funkcija klase 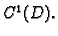 Neka je
Neka je
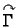 zatvorena, pozitivno
orijentirana, po dijelovima glatka krivulja u
zatvorena, pozitivno
orijentirana, po dijelovima glatka krivulja u 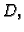 i neka je
i neka je
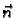 vektorska funkcija jediničnih vanjskih vektora normale na
krivulju
vektorska funkcija jediničnih vanjskih vektora normale na
krivulju 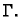 Dokažite da vrijedi
Dokažite da vrijedi
Rješenje. Vektori 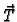 i
i 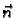 su jedinični, pa se iz slike
3.4 vidi da je,
su jedinični, pa se iz slike
3.4 vidi da je,
Slika 3.4:
Vektori tangente i normale na ravninsku krivulju.
|
|
Dakle
Zadnja jednakost vrijedi zahvaljujući Greenovom teoremu.
- 2.
- U ravnini djeluje polje sile
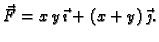 Naći rad sile po a)
pravcu
Naći rad sile po a)
pravcu 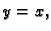 b) po paraboli
b) po paraboli 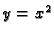 od točke
od točke 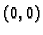 do točke
do točke
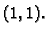
Rješenje. a) Imamo parametrizaciju
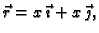
![$ x\in [0,1].$](img1976.gif) Odatle
Odatle
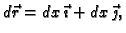 i prema tome
i prema tome
b) U ovom slučaju imamo
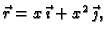
![$ x\in [0,1].$](img1976.gif) Odatle
Odatle
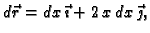 i prema tome
i prema tome
- 3.
- Izračunati površinu lika što ga omeđuju jedan luk cikloide
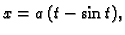
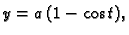
![$ t\in [0,2\pi]$](img1984.gif) i
os
i
os 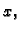 pomoću krivuljnog integrala 2. vrste.
pomoću krivuljnog integrala 2. vrste.
Rješenje.
Duž osi  imamo
imamo 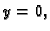 i
i 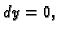 pa taj dio ne doprinosi ništa
površini. Da orijentacija ruba lika bude pozitivna, trebamo
integrirati po cikloidi od
pa taj dio ne doprinosi ništa
površini. Da orijentacija ruba lika bude pozitivna, trebamo
integrirati po cikloidi od 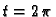 do
do 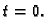 Dakle
Dakle





Next: Krivulje u prostoru
Up: Krivulje i krivuljni integrali
Previous: Krivuljni integral 1. vrste
Contents
Index
Salih Suljagic
2000-03-11
![]() glatka krivulja u prostoru (Jordanov luk). U svakoj
točki krivulje postoji tangenta.
Orijentirati
krivulju
glatka krivulja u prostoru (Jordanov luk). U svakoj
točki krivulje postoji tangenta.
Orijentirati
krivulju ![]() znači u svakoj točki krivulje odabrati jedan od
dva moguća jedinična vektora u smjeru tangente.
znači u svakoj točki krivulje odabrati jedan od
dva moguća jedinična vektora u smjeru tangente.
![]() nudi jednu takvu orijentaciju, jer je
parametrizacijom potpuno zadan vektor
nudi jednu takvu orijentaciju, jer je
parametrizacijom potpuno zadan vektor
![]() koji je
upravo jedinični vektor tangente na krivulju
koji je
upravo jedinični vektor tangente na krivulju ![]() u točki
u točki
![]() U daljnjem ćemo pretpostavljati da su
parametrizacija i orijentacija u skladu.
U daljnjem ćemo pretpostavljati da su
parametrizacija i orijentacija u skladu.
![]() zatvorena i nalazi se u ravnini, onda
kažemo da je pozitivno orijentirana, ako vektori tangente nalažu
gibanje po krivulji protivno kretanju kazaljke na satu. U suprotnom,
kažemo da je krivulja negativno orijentirana.
zatvorena i nalazi se u ravnini, onda
kažemo da je pozitivno orijentirana, ako vektori tangente nalažu
gibanje po krivulji protivno kretanju kazaljke na satu. U suprotnom,
kažemo da je krivulja negativno orijentirana.
![]() ćemo zapisivati kao
ćemo zapisivati kao
![]()
![]() glatka orijentirana krivulja
u prostoru. Neka je
glatka orijentirana krivulja
u prostoru. Neka je ![]() početna, a
početna, a ![]() završna točka krivulje. Neka
se krivulja nalazi u polju neke sile. To znači da u svakoj točki
završna točka krivulje. Neka
se krivulja nalazi u polju neke sile. To znači da u svakoj točki ![]() krivulje djeluje akceleracija
krivulje djeluje akceleracija
![]() Da bi materijalna točka
mase
Da bi materijalna točka
mase ![]() po krivulji prešla put od početne točke
po krivulji prešla put od početne točke ![]() do završne
točke
do završne
točke ![]() potrebno je izvršiti neki rad. Interesira nas koliko
iznosi potrebni rad. Da bismo ga izračunali, podijelimo krivulju
točkama
potrebno je izvršiti neki rad. Interesira nas koliko
iznosi potrebni rad. Da bismo ga izračunali, podijelimo krivulju
točkama
![]() na manje dijelove. Rad sile
duž orijentiranog luka
na manje dijelove. Rad sile
duž orijentiranog luka
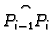 je približno
je približno
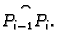 Ukupni rad je približno jednak
Ukupni rad je približno jednak
![]() područje u
područje u ![]() i
i
![]() vektorska funkcija. Neka je
vektorska funkcija. Neka je
![]() glatka orijentirana krivulja u
glatka orijentirana krivulja u
![]() tako da je
tako da je ![]() početna, a
početna, a ![]() završna točka.
Podijelimo krivulju na manje dijelove točkama
završna točka.
Podijelimo krivulju na manje dijelove točkama
![]() Na dijelu krivulje
Na dijelu krivulje
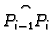 izaberimo proizvoljno točku
izaberimo proizvoljno točku ![]() i to za svaki
i to za svaki
![]() (v. sliku 3.3.1.) Uočimo sljedeću sumu
(v. sliku 3.3.1.) Uočimo sljedeću sumu
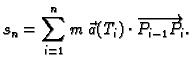
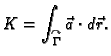
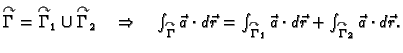
![]() glatka orijentirana
krivulja u prostoru, i neka je njezina parametrizacija
glatka orijentirana
krivulja u prostoru, i neka je njezina parametrizacija
![]() gdje je
gdje je
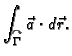
![]() na podsegmente
na podsegmente
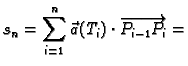
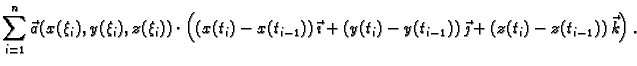
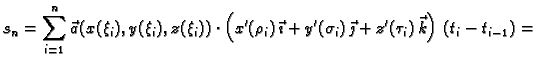
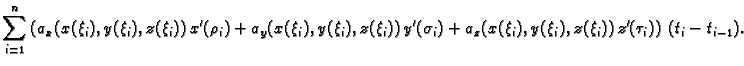
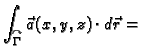
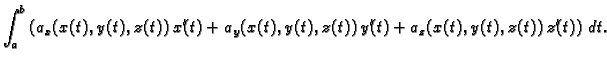
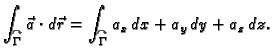
![]() Tako je
Tako je
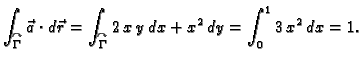
![]()
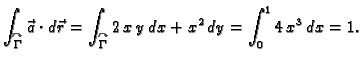
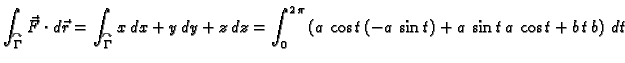
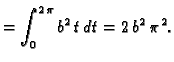
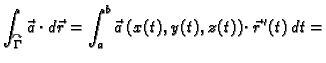
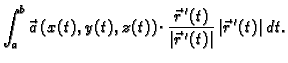
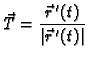
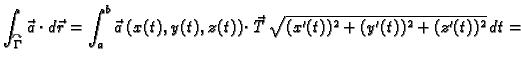
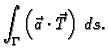
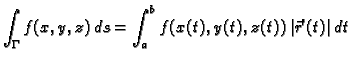
![]() u
u ![]() je područje koje ima svojstvo da se svaka zatvorena krivulja u
je područje koje ima svojstvo da se svaka zatvorena krivulja u
![]() može bez prekidanja stegnuti na točku ne izlazeći iz
može bez prekidanja stegnuti na točku ne izlazeći iz
![]() Na slici 2.3 imamo primjer područja koje
je jednostruko povezano. S druge strane na slici 1.5
imamo primjer područja koje nije jednostruko povezano. Ako opišemo
zatvorenu krivulju u području oko šupljine, onda nije moguće
stegnuti tu krivulju bez kidanja na točku ne izlazeći iz područja.
Takvo područje se zove višestruko povezano
područje.
Na slici 2.3 imamo primjer područja koje
je jednostruko povezano. S druge strane na slici 1.5
imamo primjer područja koje nije jednostruko povezano. Ako opišemo
zatvorenu krivulju u području oko šupljine, onda nije moguće
stegnuti tu krivulju bez kidanja na točku ne izlazeći iz područja.
Takvo područje se zove višestruko povezano
područje.
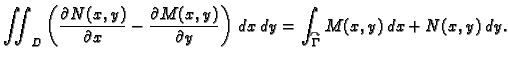
![]()
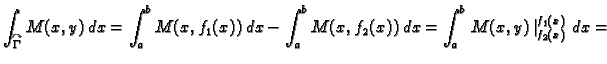
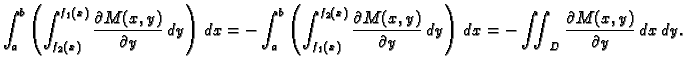
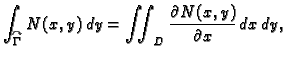
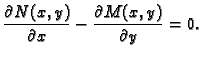
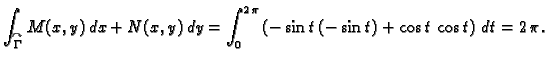
![]() i
i ![]() zadovoljavaju uvjete Greenovog
teorema,
zadovoljavaju uvjete Greenovog
teorema,
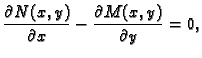
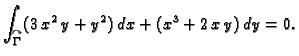
![]() u ravnini može se, zahvaljujući Greenovoj formuli, naći
površina lika
u ravnini može se, zahvaljujući Greenovoj formuli, naći
površina lika ![]() Površina lika
Površina lika ![]() je
je
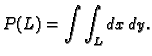
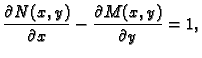
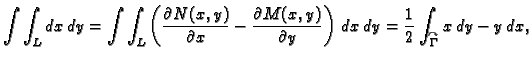
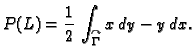
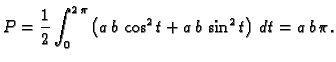
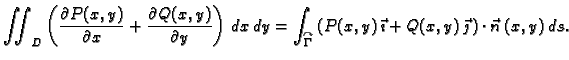
![]() i
i ![]() su jedinični, pa se iz slike
3.4 vidi da je,
su jedinični, pa se iz slike
3.4 vidi da je,
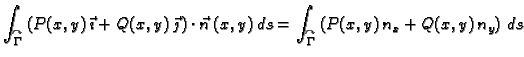
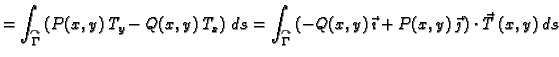
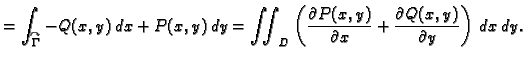
![]()
![]() Odatle
Odatle
![]() i prema tome
i prema tome
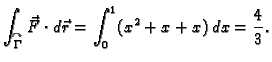
![]()
![]() Odatle
Odatle
![]() i prema tome
i prema tome