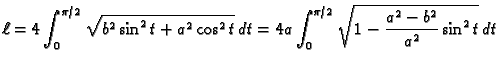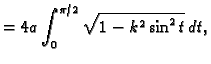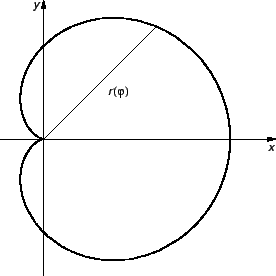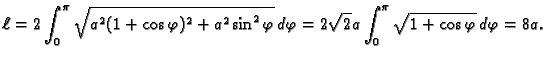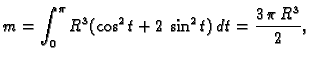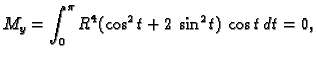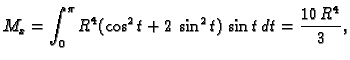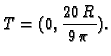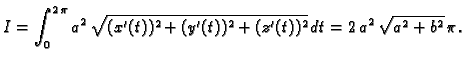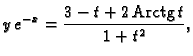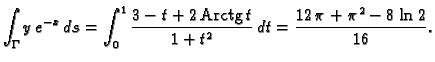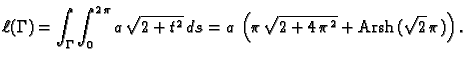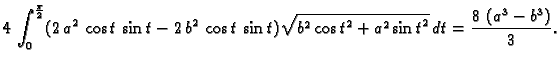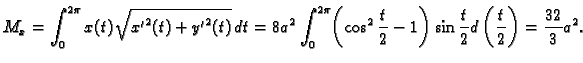Next: Krivuljni integral 2. vrste
Up: Krivulje i krivuljni integrali
Previous: Vektorske funkcije. Krivulje
Contents
Index
Subsections
Neka je  glatka krivulja u prostoru s rubnim točkama
glatka krivulja u prostoru s rubnim točkama 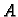 i
i
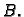 Pretpostavimo da je na krivulji definirana gustoća mase
Pretpostavimo da je na krivulji definirana gustoća mase 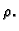 Interesira nas masa te krivulje.
Interesira nas masa te krivulje.
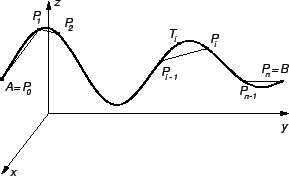
Podijelimo krivulju na manje dijelove točkama na krivulji
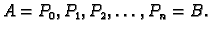 Na svakom od lukova
Na svakom od lukova
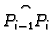 odaberimo točku
odaberimo točku 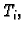
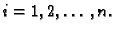 Masa luka krivulje
Masa luka krivulje
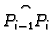 približno je jednaka
približno je jednaka
gdje je
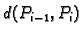 udaljenost točaka
udaljenost točaka 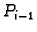 i
i 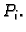 Ukupna masa je približno jednaka
Sada uzimamo sve finije podjele krivulje na manje dijelove. Očekujemo
da ćemo dobivati sve bolje aproksimacije ukupne mase krivulje.
Ukupna masa je približno jednaka
Sada uzimamo sve finije podjele krivulje na manje dijelove. Očekujemo
da ćemo dobivati sve bolje aproksimacije ukupne mase krivulje.
Ako želimo naći duljinu krivulje, onda možemo postupiti isto kao
kod mase krivulje, s tim da uzmemo da je gustoća mase 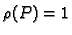 na
krivulji. Tada masa postaje brojčano jednaka duljini krivulje. Dakle
duljina krivulje je približno jednaka
na
krivulji. Tada masa postaje brojčano jednaka duljini krivulje. Dakle
duljina krivulje je približno jednaka
Očekujemo da ta suma to bolje aproksimira pravu duljinu krivulje,
što je finija podjela krivulje na manje dijelove.
Ova dva problema nas vode na definiciju krivuljnog integrala 1. vrste.
Neka je  glatka krivulja u prostoru s rubnim točkama
glatka krivulja u prostoru s rubnim točkama 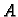 i
i
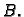 Pretpostavimo da je na krivulji definirana
funkcija
Pretpostavimo da je na krivulji definirana
funkcija 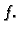 Podijelimo krivulju na manje dijelove točkama na
krivulji
Podijelimo krivulju na manje dijelove točkama na
krivulji
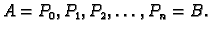 Na svakom od lukova
Na svakom od lukova
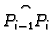 odaberimo točku
odaberimo točku 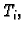
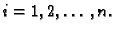
Uočimo sljedeću sumu
Taj broj ovisi o načinu
podjele krivulje na manje dijelove, i o izboru točaka 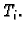 Ako
prilikom sve finijih podjela, takvih da
Ako
prilikom sve finijih podjela, takvih da
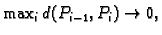
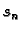 teži prema nekom broju
teži prema nekom broju
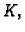 onda se taj broj zove krivuljni integral 1.
vrste funkcije
onda se taj broj zove krivuljni integral 1.
vrste funkcije  po krivulji
po krivulji 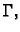 i označava s
i označava s
Ako je
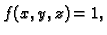 i
i 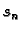 teži prema
teži prema 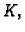 onda se kaže da
krivulja
onda se kaže da
krivulja  ima duljinu, i broj
ima duljinu, i broj
se zove duljina krivulje
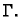
Ako je
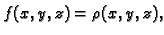 gustoća mase materijalne krivulje
gustoća mase materijalne krivulje
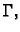 i
i 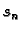 teži prema
teži prema 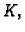 onda se kaže da materijalna
krivulja
onda se kaže da materijalna
krivulja  ima masu, i broj
ima masu, i broj
se zove masa krivulje
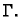
- 1.
-
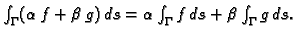
- 2.
-
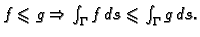
- 3.
-
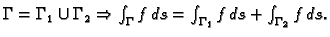
Dakle krivuljni integral 1. vrste rješava problem duljine
(kad je
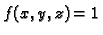 ) i mase krivulje (kad je
) i mase krivulje (kad je
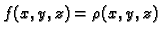 ), ali također
i neke druge probleme. Na primjer, ako je
), ali također
i neke druge probleme. Na primjer, ako je
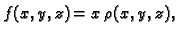
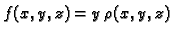 ili
ili
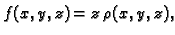 onda se
pomoću krivuljnog integrala 1. vrste računaju statički momenti
materijalne krivulje u odnosu na koordinatne ravnine
onda se
pomoću krivuljnog integrala 1. vrste računaju statički momenti
materijalne krivulje u odnosu na koordinatne ravnine
i pomoću njih težište materijalne krivulje
Također se krivuljnim integralom računaju momenti inercije krivulje
sa zadanom gustoćom mase.
Računanje krivuljnog integrala 1. vrste
Neka je  glatka krivulja u prostoru, i neka je njezina
parametrizacija
glatka krivulja u prostoru, i neka je njezina
parametrizacija
![$ ([a,b],\vec{r}\,),$](img1786.gif) gdje je
gdje je
Neka je na  zadana funkcija
zadana funkcija
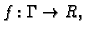 takva da postoji
takva da postoji
Podijelimo segment ![$ [a,b]$](img986.gif) na podsegmente
na podsegmente
Tako dobivamo točke na krivulji
Izaberimo
![$ \xi_i\in [t_{i-1},t_i]$](img1792.gif) proizvoljno, i neka je
proizvoljno, i neka je
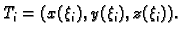 Tada je
Prema Lagrangeovom teoremu srednje vrijednosti, postoje
Tada je
Prema Lagrangeovom teoremu srednje vrijednosti, postoje
![$ \rho_i,
\sigma_i, \tau_i\in [t_{i-1},t_i]$](img1796.gif) takvi da je
za svaki
takvi da je
za svaki
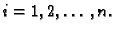 Slijedi
Ovo je integralna suma za funkciju
Slijedi
Ovo je integralna suma za funkciju
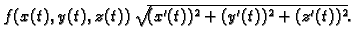 Prema
tome krivuljni integral 1. vrste se računa po formuli
Prema
tome krivuljni integral 1. vrste se računa po formuli
Ako je krivulja  ravninska, i pri tom graf funkcije
ravninska, i pri tom graf funkcije
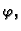 za parametar možemo uzeti
za parametar možemo uzeti 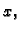
pa se integral računa po formuli
Ako je krivulja u
ravnini zadana u polarnom sustavu jednadžbom
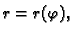 onda za
parametar možemo uzeti
onda za
parametar možemo uzeti 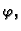
i odatle slijedi formula
Primjer 3.7
Naći duljinu luka parabole
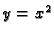
od
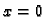
do
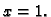
Rješenje.
Primjer 3.8
Duljina elipse, parametarski zadane s
je
gdje je
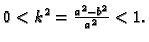
Ovaj integral nije elementaran,
tako da ga ne možemo rješavati uobičajenim metodama. Jedan od
načina kako ga možemo približno izračunati je razvojem
podintegralne funkcije u red, i zatim integriranjem član po član.
Primjer 3.9
Izračunajmo duljinu kardioide
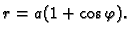
Rješenje.
Primjer 3.10
Naći težište žice savijene u obliku gornje središnje
polukružnice radiusa
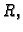
gustoće mase
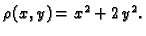
Rješenje. Za parametrizaciju žice možemo uzeti
Tada je
pa je težište
Primjer 3.11
Naći moment inercije jednog zavoja helikoide konstantne gustoće
mase
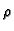
u odnosu na os helikoide (os
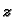
).
Rješenje. Parametrizacija jednog zavoja helikoide je
Kvadrat udaljenosti točke
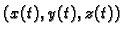
helikoide od osi je
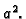
Tako je moment inercije
- 1.
- Što je duljina krivulje, i kako se računa?
- 2.
- Definirajte krivuljni integral 1. vrste.
- 3.
- Koji problem rješava krivuljni integral 1. vrste?
- 4.
- Kako se računa krivuljni integral 1. vrste?
- 5.
- Koja svojstva ima krivuljni integral 1. vrste?
- 1.
- Izračunati integral
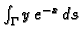 po krivulji
po krivulji
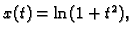
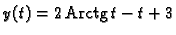 između točaka
između točaka 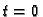 i
i
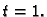
Rješenje.
pa je
- 2.
- Naći duljinu prvog zavoja helikoide namotane na stožac
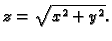
Rješenje. Treba biti
pa ako je
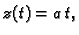 onda iz
onda iz
 slijedi
parametrizacija
slijedi
parametrizacija
- 3.
- Naći masu žice savijene u obliku elipse s poluosima
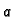 i
i
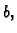
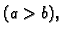 ako je gustoća mase
ako je gustoća mase
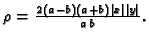
Rješenje. Parametrizacija elipse je
pa je masa
- 4.
- Naći statički moment prvog luka cikloide u odnosu na os
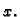
Rješenje.





Next: Krivuljni integral 2. vrste
Up: Krivulje i krivuljni integrali
Previous: Vektorske funkcije. Krivulje
Contents
Index
Salih Suljagic
2000-03-11
![]() glatka krivulja u prostoru s rubnim točkama
glatka krivulja u prostoru s rubnim točkama ![]() i
i
![]() Pretpostavimo da je na krivulji definirana gustoća mase
Pretpostavimo da je na krivulji definirana gustoća mase ![]() Interesira nas masa te krivulje.
Interesira nas masa te krivulje.
![]() Na svakom od lukova
Na svakom od lukova
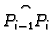 odaberimo točku
odaberimo točku ![]()
![]() Masa luka krivulje
Masa luka krivulje
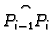 približno je jednaka
približno je jednaka
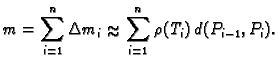
![]() na
krivulji. Tada masa postaje brojčano jednaka duljini krivulje. Dakle
duljina krivulje je približno jednaka
na
krivulji. Tada masa postaje brojčano jednaka duljini krivulje. Dakle
duljina krivulje je približno jednaka
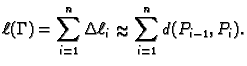
![]() glatka krivulja u prostoru s rubnim točkama
glatka krivulja u prostoru s rubnim točkama ![]() i
i
![]() Pretpostavimo da je na krivulji definirana
funkcija
Pretpostavimo da je na krivulji definirana
funkcija ![]() Podijelimo krivulju na manje dijelove točkama na
krivulji
Podijelimo krivulju na manje dijelove točkama na
krivulji
![]() Na svakom od lukova
Na svakom od lukova
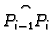 odaberimo točku
odaberimo točku ![]()
![]()
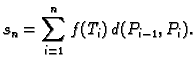
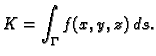
![]() i
i ![]() teži prema
teži prema ![]() onda se kaže da
krivulja
onda se kaže da
krivulja ![]() ima duljinu, i broj
ima duljinu, i broj
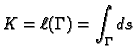
![]() gustoća mase materijalne krivulje
gustoća mase materijalne krivulje
![]() i
i ![]() teži prema
teži prema ![]() onda se kaže da materijalna
krivulja
onda se kaže da materijalna
krivulja ![]() ima masu, i broj
ima masu, i broj
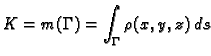
![]() ) i mase krivulje (kad je
) i mase krivulje (kad je
![]() ), ali također
i neke druge probleme. Na primjer, ako je
), ali također
i neke druge probleme. Na primjer, ako je
![]()
![]() ili
ili
![]() onda se
pomoću krivuljnog integrala 1. vrste računaju statički momenti
materijalne krivulje u odnosu na koordinatne ravnine
onda se
pomoću krivuljnog integrala 1. vrste računaju statički momenti
materijalne krivulje u odnosu na koordinatne ravnine
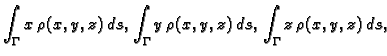
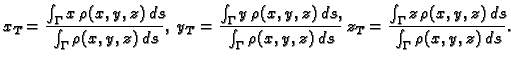
![]() glatka krivulja u prostoru, i neka je njezina
parametrizacija
glatka krivulja u prostoru, i neka je njezina
parametrizacija
![]() gdje je
gdje je
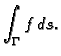
![]() na podsegmente
na podsegmente
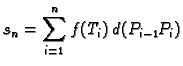
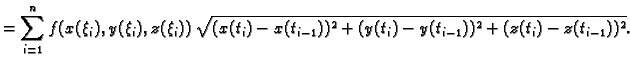
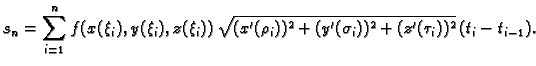
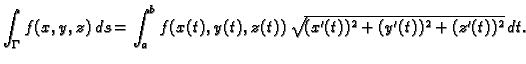
![]() ravninska, i pri tom graf funkcije
ravninska, i pri tom graf funkcije
![]() za parametar možemo uzeti
za parametar možemo uzeti ![]()
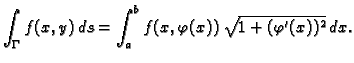
![]() onda za
parametar možemo uzeti
onda za
parametar možemo uzeti ![]()
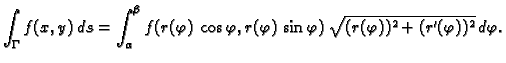
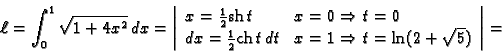
![% latex2html id marker 39657
$\displaystyle \frac{1}{2}\int_0^{\ln(2+\sqrt{5})}{...
...\right]_0^{\ln(2+\sqrt{5})}=
\frac{1}{4}\left[2\sqrt{5}+\ln(2+\sqrt{5})\right].$](img1813.gif)