




Next: Linearna diferencijalna jednadžba 1.
Up: Obične diferencijalne jednadžbe
Previous: Obične diferencijalne jednadžbe
Contents
Index
Subsections
Definicija 45
Neka je

područje u
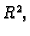
neka je
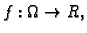
neprekidna funkcija na

. Jednadžbu
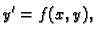 |
(6.1) |
gdje je
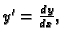
zovemo
običnom diferencijalnom jednadžbom 1. reda.
Osnovni problem je riješiti diferencijalnu jednadžbu (6.1),
a to znači naći funkciju 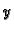 klase
klase 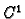 na nekom intervalu
na nekom intervalu
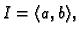 tako da je
tako da je
- 1.
-

- 2.
-
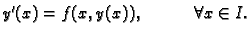
Takva funkcija, ako postoji, zove se rješenje jednadžbe
(6.1).
Ako je 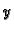 rješenje jednadžbe (6.1) i
rješenje jednadžbe (6.1) i 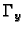 njezin
graf, onda je jednadžbom (6.1) određen koeficijent smjera
tangente na
njezin
graf, onda je jednadžbom (6.1) određen koeficijent smjera
tangente na 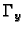 u točki
u točki 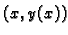 , i to za svaki
, i to za svaki 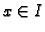 .
Općenito je jednadžbom (6.1) u svakoj točki
.
Općenito je jednadžbom (6.1) u svakoj točki
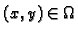 zadan koeficijent smjera
zadan koeficijent smjera 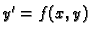 tangente na neku
krivulju. Stoga kažemo da je jednadžbom (6.1) zadano na
tangente na neku
krivulju. Stoga kažemo da je jednadžbom (6.1) zadano na
 polje
smjerova (v. sl. 6.1).
polje
smjerova (v. sl. 6.1).
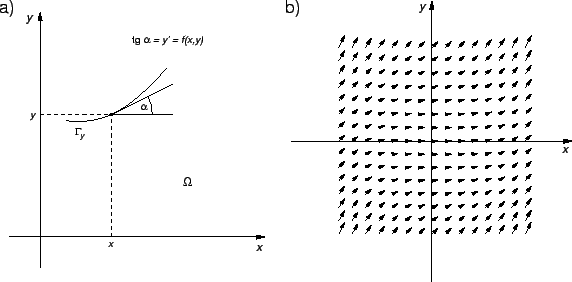
Slika 6.1:
a) Geometrijsko značenje diferencijalne jednadžbe.
b) Polje smjerova diferencijalne jednadžbe
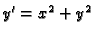 na području
na području
![$ [-1,1]\times {}[-1,1].$](img10.gif)
|
|
Za neki
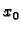 općenito postoji beskonačno mnogo
općenito postoji beskonačno mnogo 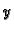 takvih da je
takvih da je
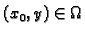 i u svakoj točki postoji smjer. Odatle se može
naslutiti da postoji mnogo rješenja diferencijalne jednadžbe (6.1).
Da se to zaista događa, pokazuje sljedeći primjer.
i u svakoj točki postoji smjer. Odatle se može
naslutiti da postoji mnogo rješenja diferencijalne jednadžbe (6.1).
Da se to zaista događa, pokazuje sljedeći primjer.
Primjer 6.1
Treba riješiti diferencijalnu jednadžbu
Rješenje. Očito 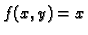 i podrazumijeva se da je
i podrazumijeva se da je
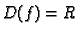 . Funkcija
. Funkcija
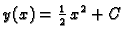 je rješenje na cijelom R i to za bilo koju
konstantu
je rješenje na cijelom R i to za bilo koju
konstantu 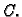
Ipak u prethodnom primjeru postoji samo jedna funkcija, rješenje,
takva da je 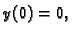 tj. rješenje čiji graf prolazi točkom
tj. rješenje čiji graf prolazi točkom
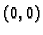 . To pokazuje da govoriti o samo jednom rješenju ima smisla
ako stavimo neki dodatni uvjet. S tim u vezi imamo sljedeću
definiciju.
. To pokazuje da govoriti o samo jednom rješenju ima smisla
ako stavimo neki dodatni uvjet. S tim u vezi imamo sljedeću
definiciju.
Definicija 46
Problem početnog uvjeta ili
Cauchyjev problem se
sastoji u tome da za danu točku
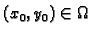
treba naći
interval
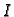
i funkciju
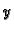
na
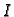
tako da je
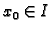
i
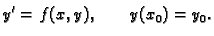 |
(6.2) |
Jednakost
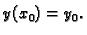 |
(6.3) |
se zove početni uvjet.
Drugim riječima Cauchyjev problem je problem da se nađe ono
rješenje diferencijalne jednadžbe (6.1) koje zadovoljava
početni uvjet (6.3).
Primjer 6.2
Treba riješiti Cauchyjev problem
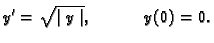 |
(6.4) |
Rješenje. Za 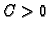 stavimo
stavimo
Lako je provjeriti da funkcija
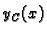
rješava Cauchyjev problem (
6.4)
ma kakav bio
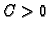
. Zatim, očito
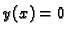
, za svaki
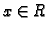
, rješava
(
6.4).
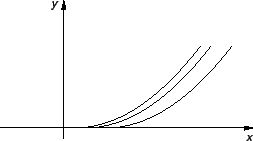
Grafovi nekih funkcija 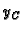 su dani na sljedećoj slici
su dani na sljedećoj slici
Vidimo da Cauchyjev problem (6.4) ima beskonačno mnogo rješenja.
Dakle, zadavanje početnog uvjeta još ne garantira jedinstvenost rješenja.
U daljnjem razmatramo specijalne slučajeve običnih diferencijalnih
jednadžbi 1. reda u kojima Cauchyjev problem ima jedno i samo jedno
rješenje, tj. rješenje postoji i jedinstveno je.
Teorem 25
Neka je
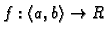
nepekidna funkcija na
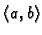
,
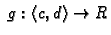
neprekidna
na
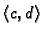
i
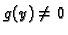
za svaki
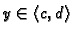
.
Tada, za svaki par brojeva
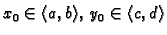
, Cauchyjev problem
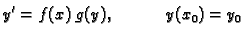 |
(6.5) |
ima jedno i samo jedno rješenje.
Slika 6.2:
Područje početnog uvjeta linearnu diferencijalnu jednadžbu kod koje se mogu separirati varijable.
|
|
Dokaz. Zbog
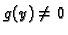 jednadžbu možemo
prepisati u obliku
jednadžbu možemo
prepisati u obliku
Pretpostavimo da je 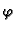 rješenje. Tada
Po teoremu o integraciji supstitucijom (v. 44)
Neka je
rješenje. Tada
Po teoremu o integraciji supstitucijom (v. 44)
Neka je 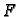 primitivna od
primitivna od  , a
, a 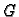 primitivna od
primitivna od
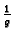 . Tada je
. Tada je
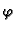 je rješenje, pa je tako
je rješenje, pa je tako
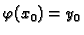 . Dakle
. Dakle
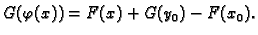 |
(6.6) |
Formula (6.6) očito ne ovisi o tome koje primitivne funkcije 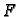 i
i 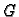 uzmemo. Iz neprekidnosti
uzmemo. Iz neprekidnosti 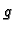 na
na
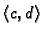 i
i
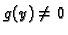 za
za
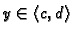 slijedi
ili
Prema tome (v. 43) je
slijedi
ili
Prema tome (v. 43) je 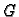 strogo monotona funkcija na
strogo monotona funkcija na
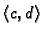 . Tako
postoji inverzna funkcija
. Tako
postoji inverzna funkcija 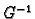 . Dakle iz (6.6)
. Dakle iz (6.6)
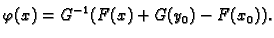 |
(6.7) |
Iz pretpostavke da je 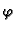 rješenje dobili smo formulu
(6.7).Budući da ta formula određuje jednu funkciju,
zaključujemo da rješenje postoji, a budući da formula (6.6) pa
prema tome i (6.7) ne ovise o tome koje funkcije
rješenje dobili smo formulu
(6.7).Budući da ta formula određuje jednu funkciju,
zaključujemo da rješenje postoji, a budući da formula (6.6) pa
prema tome i (6.7) ne ovise o tome koje funkcije 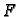 i
i 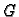 izaberemo, zaključujemo da je rješenje jedinstveno.
izaberemo, zaključujemo da je rješenje jedinstveno.

Ako nije zadan početni uvjet, onda su 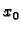 i
i 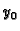 u formuli
(6.7) neodređeni (osim što su vezani zahtjevom
u formuli
(6.7) neodređeni (osim što su vezani zahtjevom
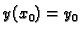 ), pa prema tome imamo
), pa prema tome imamo
gdje je 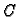 neodređena konstanta.
neodređena konstanta.
Definicija 47
Neka je
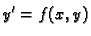 |
(6.8) |
obična diferencijalna jednadžba 1. reda. Skup funkcija
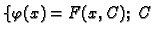 konstanta konstanta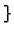 |
(6.9) |
takav da proizvoljnim izborom konstante
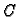
možemo dobiti rješenje
jednadžbe (
6.8) zovemo
općim
rješenjem jednadžbe (
6.8).
Primjer 6.3
Treba riješiti Cauchyjev problem
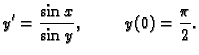 |
(6.10) |
Rješenje. Imamo
Dakle
Funkcija
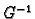
postoji na intervalu
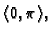
i
jednaka je
pa imamo
Interval
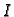
na kojem je zadano rješenje je određen s
Odatle
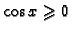
, pa je zbog početnog uvjeta taj interval
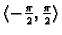
, tj. rješenje je funkcija
zadana formulom
Na sljedećoj slici vidimo polje smjerova ove diferencijalne
jednadžbe, točku određenu početnim uvjetom, i graf rješenja.
Slika 6.3:
Polje smjerova i rješenje.
|
|
Ako je u diferencijalnoj jednadžbi (6.1)
onda takvu jednadžbu, tj. jednadžbu
zovemo homogenom diferencijalnom
jednadžbom 1. reda.
Stavimo
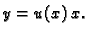 Tada
a to je slučaj kad se mogu separirati varijable, naravno uz dodatni uvjet
Tada
a to je slučaj kad se mogu separirati varijable, naravno uz dodatni uvjet
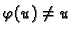 . Tako imamo sljedeći teorem.
. Tako imamo sljedeći teorem.
Teorem 26
Neka je
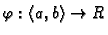
neprekidna
funkcija i neka je
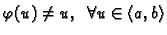
. Tada, za svaki par brojeva
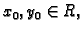
takvih da
je
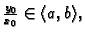
(v. sl.
6.4) postoji jedno i samo jedno rješenje
Cauchyjevog problema
 |
(6.11) |
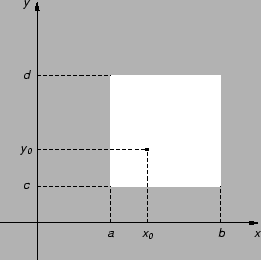
Slika 6.4:
Područje početnog uvjeta za homogenu diferencijalnu jednadžbu.
|
|
Primjer 6.4
Riješimo diferencijalnu jednadžbu
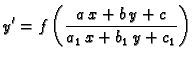 |
(6.12) |
Rješenje. 1. slučaj. Pretpostavimo da je
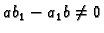 . Tada sustav
. Tada sustav
ima jedinstveno rješenje
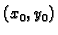
i vrijedi
Stavimo
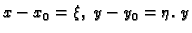
je funkcija od

, a

od
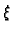
pa je tako
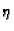
funkcija od
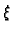
.
Dakle
Tako smo jednadžbu (
6.12) sveli na homogenu.
2. slučaj.
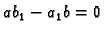 . Tada je
. Tada je
pa je
Stavimo
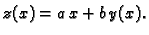
i odatle
tj.
a to je specijalan slučaj separacije varijabli.
- 1.
- Što je obična diferencijalna jednadžba 1. reda?
- 2.
- Što znači riješiti običnu diferencijalnu jednadžbu 1. reda?
Što je rješenje?
- 3.
- Polje smjerova. Interpretirajte geometrijski običnu
diferencijalnu jednadžbu 1. reda.
- 4.
- Definirajte Cauchyjev problem (problem početnog uvjeta) za
običnu diferencijalnu jednadžbu 1. reda.
- 5.
- Da li zadavanje početnog uvjeta osigurava jedinstvenost
rješenja? Primjer.
- 6.
- Iskažite teorem o postojanju i jedinstvenosti rješenja
diferencijalne jednadžbe koja spada u klasu jednadžbi kod kojih se
mogu separirati varijable. Da li ga možete dokazati?
- 7.
- Što je opće rješenje obične diferencijalne jednadžbe 1. reda?
- 8.
- Kako izgleda homogena diferencijalna jednadžba 1. reda? Kako se
rješava?
- 9.
- U kojem području se može birati početni uvjet za homogenu
diferencijalnu jednadžbu?
- 1.
- U posudu, koja sadrži
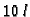 vode, ulijeva se otopina, koja
sadrži
vode, ulijeva se otopina, koja
sadrži 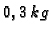 soli po jednoj litri, brzinom od
soli po jednoj litri, brzinom od 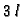 u
minuti. Otopina se potpuno izmiješa i nakon toga istječe iz posude
brzinom od također
u
minuti. Otopina se potpuno izmiješa i nakon toga istječe iz posude
brzinom od također 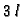 u minuti. Koliko će soli biti u posudi
kada
u minuti. Koliko će soli biti u posudi
kada
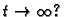 Kada će u posudi biti polovina te
količine?
Kada će u posudi biti polovina te
količine?
Rješenje. Označimo s 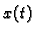 količinu soli u otopini u trenutku
količinu soli u otopini u trenutku 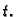 Količina soli, koja uđe u vremenskom intervalu
Količina soli, koja uđe u vremenskom intervalu 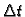 minuta, je
minuta, je
Količina soli, koja izađe u vremenskom intervalu 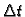 minuta,
je
Dakle, prirast količine soli u vremenskom intervalu od
minuta,
je
Dakle, prirast količine soli u vremenskom intervalu od 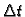 minuta iznosi
minuta iznosi
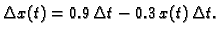 |
(6.13) |
Ovo je približni račun koji je to točniji što je manji vremenski
interval
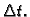 Stoga podijelimo jednadžbu (6.13) s
Stoga podijelimo jednadžbu (6.13) s
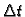 i pustimo da
i pustimo da
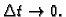 Dobivamo
Na početku je u posudi bilo
Dobivamo
Na početku je u posudi bilo 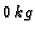 soli. Tako imamo sljedeći
Cauchyjev problem
soli. Tako imamo sljedeći
Cauchyjev problem
Ovaj problem se očito može riješiti separacijom varijabli. Pri tom
je
Odatle
Iz
dobit ćemo inverznu funkciju 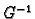 tako da
tako da  izrazimo kao
funkciju od
izrazimo kao
funkciju od 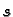 Prema formuli (6.7), uzimajući u obzir da je
Prema formuli (6.7), uzimajući u obzir da je 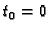 i
i
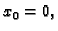 i uvrštavajući
imamo rješenje
i uvrštavajući
imamo rješenje
Kad vrijeme raste u beskonačnost, imamo
Dakle količina soli u otopini teži prema iznosu od 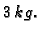
Da dobijemo vrijeme kad će biti polovica te količine, treba
izračunati 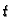 iz jednadžbe
iz jednadžbe
što daje
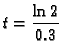
min.
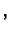
jer su jedinice u kojima smo
izvodili jednadžbu bile kilogram i minuta.





Next: Linearna diferencijalna jednadžba 1.
Up: Obične diferencijalne jednadžbe
Previous: Obične diferencijalne jednadžbe
Contents
Index
Salih Suljagic
2000-03-11
![]() klase
klase ![]() na nekom intervalu
na nekom intervalu
![]() tako da je
tako da je
![]() i podrazumijeva se da je
i podrazumijeva se da je
![]() . Funkcija
. Funkcija
![]() je rješenje na cijelom R i to za bilo koju
konstantu
je rješenje na cijelom R i to za bilo koju
konstantu ![]()
![]() tj. rješenje čiji graf prolazi točkom
tj. rješenje čiji graf prolazi točkom
![]() . To pokazuje da govoriti o samo jednom rješenju ima smisla
ako stavimo neki dodatni uvjet. S tim u vezi imamo sljedeću
definiciju.
. To pokazuje da govoriti o samo jednom rješenju ima smisla
ako stavimo neki dodatni uvjet. S tim u vezi imamo sljedeću
definiciju.
![]() stavimo
stavimo
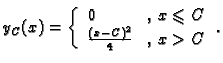
![]() su dani na sljedećoj slici
su dani na sljedećoj slici
![]() jednadžbu možemo
prepisati u obliku
jednadžbu možemo
prepisati u obliku
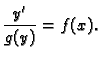
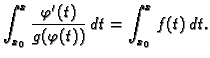
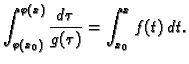
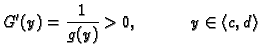
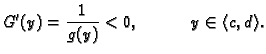
![]() i
i ![]() u formuli
(6.7) neodređeni (osim što su vezani zahtjevom
u formuli
(6.7) neodređeni (osim što su vezani zahtjevom
![]() ), pa prema tome imamo
), pa prema tome imamo
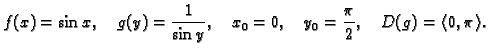
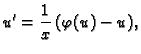
![]() . Tada sustav
. Tada sustav
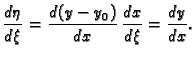
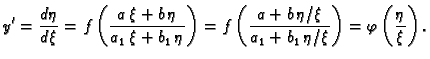
![]() . Tada je
. Tada je
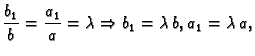
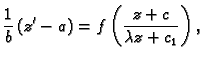
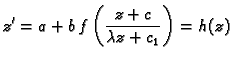
![]() količinu soli u otopini u trenutku
količinu soli u otopini u trenutku ![]() Količina soli, koja uđe u vremenskom intervalu
Količina soli, koja uđe u vremenskom intervalu ![]() minuta, je
minuta, je
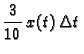 kg
kg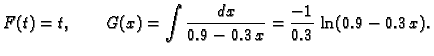
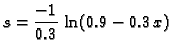
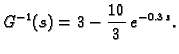
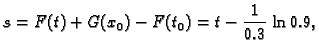
![]() iz jednadžbe
iz jednadžbe
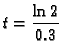 min.
min.