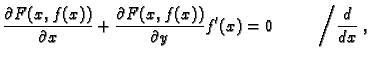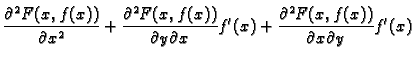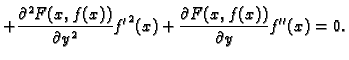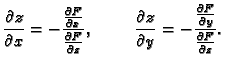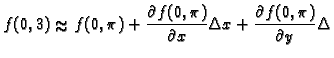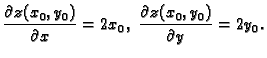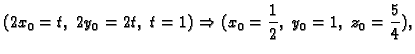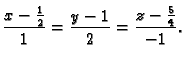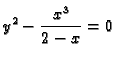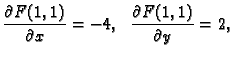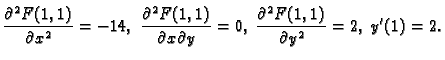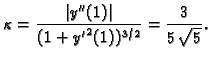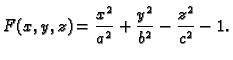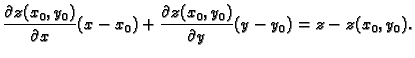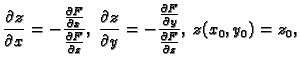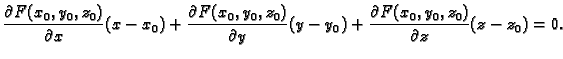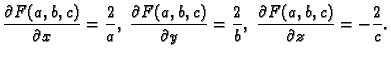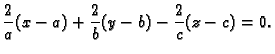



Next: Taylorov teorem srednje vrijednosti
Up: Diferencijalni račun
Previous: Derivacije funkcija više varijabli
Contents
Index
Subsections
Teorem srednje vrijednosti
Teorem 7
[
3] Neka je
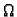
područje u
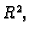
i neka je
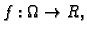
klase
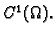
Neka su točke
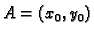
i
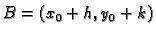
u
takve, da spojnica
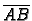
leži u
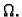
Tada postoji točka
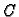
na
spojnici
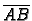
takva, da je
Dokaz. Stavimo
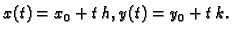 Budući da je
Budući da je 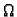 otvoren skup, i da spojnica
otvoren skup, i da spojnica
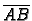 leži u
leži u 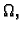 postoji
postoji
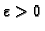 takav da
točke
takav da
točke
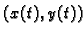 leže u
leže u 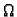 za svaki
za svaki
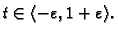 Na tom intervalu je
složena funkcija
Na tom intervalu je
složena funkcija
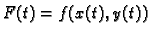 neprekidno derivabilna, pa
ispunjava uvjete Lagrangeovog teorema srednje vrijednosti. Tako
postoji
neprekidno derivabilna, pa
ispunjava uvjete Lagrangeovog teorema srednje vrijednosti. Tako
postoji
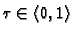 takav da vrijedi
takav da vrijedi
Formula iz teorema daje prirast funkcije 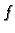 u točki
u točki 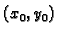
Možemo birati različite 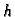 i
i 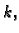 tj. možemo iz točke
tj. možemo iz točke
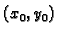 krenuti u raznim smjerovima i različito daleko. Jedini
uvjet je da ne izađemo iz
krenuti u raznim smjerovima i različito daleko. Jedini
uvjet je da ne izađemo iz 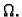 Naravno, u svakom pojedinom
slučaju imamo neku novu točku na odgovarajućoj spojnici.
Problem je u tome što ne znamo koju točku
Naravno, u svakom pojedinom
slučaju imamo neku novu točku na odgovarajućoj spojnici.
Problem je u tome što ne znamo koju točku 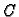 na spojnici
treba uzeti. Zato se umjesto točnom služimo približnom formulom
Ova formula se zove
formula konačnih prirasta.
Formulu konačnih prirasta koristimo za približno računanje.
na spojnici
treba uzeti. Zato se umjesto točnom služimo približnom formulom
Ova formula se zove
formula konačnih prirasta.
Formulu konačnih prirasta koristimo za približno računanje.
Primjer 1.29
Koliko se izmijeni površina kružnog isječka, ako se
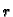
promijeni za
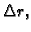
a
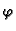
za
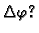
Rješenje.
Površina je
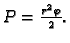
Postojanje parcijalnih derivacija nije osobito jak zahtjev na
funkciju, kao što pokazuje sljedeći primjer
Primjer 1.30
Neka je
Imamo
Dakle, parcijalne derivacije postoje u točki
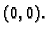
Međutim, u
primjeru
1.17 smo vidjeli da ova funkcija nema limes u
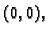
i prema tome nije neprekidna u
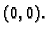
To pokazuje da postojanje
parcijalnih derivacija ne osigurava čak niti neprekidnost. Podsjetimo
se da je postojanje derivacije u slučaju funkcije jedne varijable
osiguravalo neprekidnost.
Sljedećom definicijom rješavamo te probleme na adekvatniji način,
uvodeći pojam derivacije i derivabilnosti funkcije.
Definicija 12
Kažemo da je
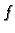 derivabilna (diferencijabilna) u točki
derivabilna (diferencijabilna) u točki
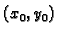
, ako postoji polinom prvog stupnja
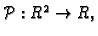
takav, da je
Polinom
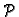
se zove
derivacija (diferencijal) funkcije 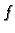 u točki
u točki
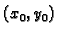
, i označava s
Teorem 8
Neka je
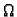
područje u
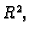
i neka je
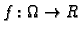
derivabilna u točki
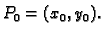
Tada
je
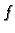
neprekidna u
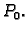
Dokaz.
Teorem 9
Neka je
područje u
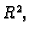
neka je
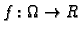
derivabilna u točki
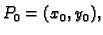
i neka
je
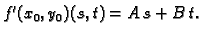
Tada postoje parcijalne derivacije
od
u točki
i
Dokaz.
Ispitivati derivabilnost funkcije po definiciji nije jednostavno, jer
treba računati odgovarajući limes. Zato se postavlja pitanje da li
se derivabilnost može ustanoviti jednostavnije. Sljedeći teorem
rješava to pitanje.
Teorem 10
Neka je
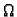
područje u
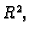
i neka
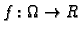
ima neprekidne parcijalne derivacije po
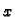
i
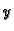
na
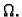
Tada je
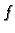
derivabilna u svakoj točki
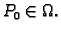
Dokaz.
Na sličan način bismo mogli definirati derivaciju funkcije od tri
varijable u točki
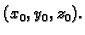 U tom slučaju to je polinom 1.
stupnja od tri varijable, označavamo ga s
U tom slučaju to je polinom 1.
stupnja od tri varijable, označavamo ga s
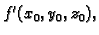 ili
ili
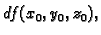 i uz uvjet da su parcijalne derivacije
neprekidne, vrijedi
i uz uvjet da su parcijalne derivacije
neprekidne, vrijedi
Definicija 13
Neka je
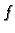
derivabilna funkcija u
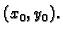
Graf
polinoma prvog stupnja
se zove
tangencijalna
ravnina na graf funkcije 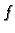 (plohu) u točki
(plohu) u točki
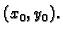
Pravac kroz točku 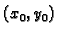 okomit na tangencijalnu ravninu se zove
normala na graf funkcije
okomit na tangencijalnu ravninu se zove
normala na graf funkcije 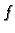 (na plohu) u točki
(na plohu) u točki
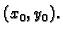
Iz ove definicije slijedi da je jednadžba tangencijalne ravnine
funkcije 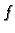 u točki
u točki 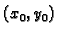
a kanonske jednadžbe normale su
Primjer 1.31
Naći jednadžbu one tangencijalne ravnine na plohu
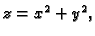
koja prolazi pravcem
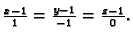
Rješenje. Tangencijalna ravnina ima jednadžbu
Ne znamo točku
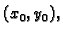
ali znamo da zadani pravac mora ležati u toj
ravnini. To znači da točka
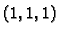
leži u ravnini, tj. zadovoljava jednadžbu tangencijalne ravnine
Vektor smjera pravca
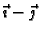
je okomit na vektor normale ravnine, dakle njihov skalarni produkt je
Odatle
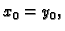
i
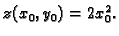
Uvrstimo, dobivamo
Tako je
Dobili smo dvije točke na plohi. To znači da se kroz zadani pravac
mogu na plohu povući dvije tangencijalne ravnine. Njihove jednadžbe su
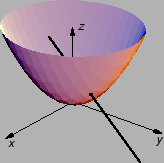
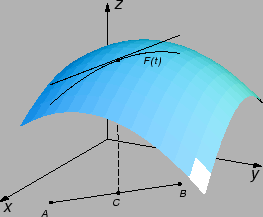
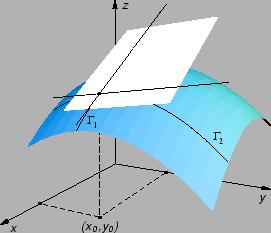
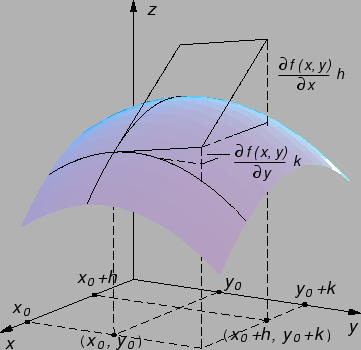
Formula konačnih prirasta,
umjesto
pravog prirasta funkcije računa prirast derivacije (diferencijala)
funkcije uzetog u točki 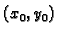 Na slici to znači,
uzimajući u obzir geometrijsku interpretaciju parcijalnih derivacija,
prirast po tangencijalnoj ravnini.
Na slici to znači,
uzimajući u obzir geometrijsku interpretaciju parcijalnih derivacija,
prirast po tangencijalnoj ravnini.
Teorem o implicitno zadanim funkcijama
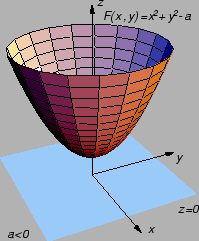
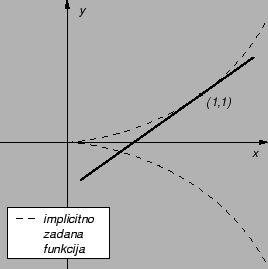
Primjer 1.32
Neka je dana funkcija od dvije varijable
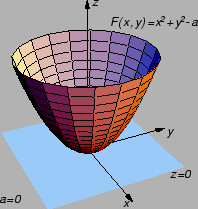
Jednadžba
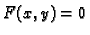
predstavlja u
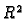
jednadžbu skupa točaka
u ravnini
Ako je
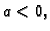
onda jednadžba nema rješenja u
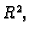
tj. ravnina
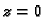
ne siječe plohu
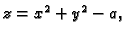
pa je
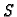
prazan skup.
Za
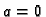
jednadžba ima samo jedno rješenje
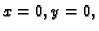
tj.
ravnina
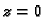
dira plohu
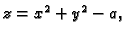
pa je
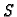
jednočlan skup
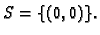
Ti slučajevi nisu interesantni. Pretpostavimo dakle, da je 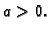 U
tom slučaju imamo više rješenja, tj. ravnina
U
tom slučaju imamo više rješenja, tj. ravnina 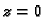 siječe plohu
siječe plohu
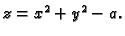
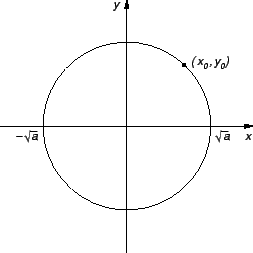
U ravnini
skup
je kružnica sa središtem u ishodištu i
radiusom
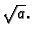
U tom slučaju apscisu
točke
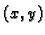
možemo birati u segmentu
![$ [-\sqrt{a},\sqrt{a}].$](img617.gif)
Izabravši apscisu
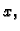
ordinatu
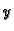
više ne možemo proizvoljno
birati, jer je jednadžbom
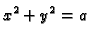 |
(1.1) |
dana veza između
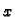
i
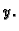
Interesiraju nas uvjeti pod kojima ta
veza postaje funkcijska, tj. takva da svakom
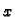
pripada po jedan
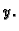
Rješavajući jednadžbu 1.1 po 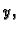 imamo
imamo
Za svaki
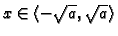
možemo birati jedan od ova dva
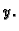
Na taj način vidimo da ima beskonačno mnogo mogućih funkcija
zadanih jednadžbom
1.1. Ako zahtijevamo da funkcija bude
neprekidna, onda imamo samo dvije mogućnosti, jer izabravši jednom
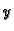
na jednoj od dvije polukružnice (gornjoj ili donjoj), moramo i za
svaki drugi
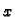
birati
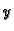
na istoj polukružnici. Konačno, ako
želimo imati samo jednu neprekidnu funkciju, onda moramo odrediti
točku
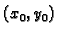
koja mora pripadati grafu funkcije, i pri tom
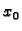
ne smije biti
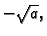
ili
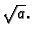
Točke
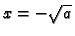
i
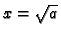
se nalaze na obje polukružnice, tako da izabravši neku
od njih još uvijek nismo odredili o kojoj se funkciji radi. To je
posljedica toga da je
Uvjerite se u to
koristeći geometrijsku interpretaciju parcijalne derivacije.
U općem slučaju problem rješava sljedeći teorem.
Teorem 11
Neka je
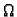
područje u
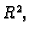
i neka je
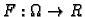
funkcija klase
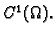
Neka postoji točka
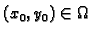
takva, da je
i neka je
Tada postoji interval
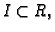
koji sadrži
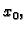
i funkcija
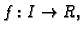
klase
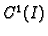
takva, da je
i vrijedi
Dokaz.
Moglo bi se pomisliti da zahtijevanje postojanja samo jedne točke
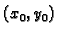 takve da je
takve da je
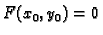 može dovesti do jednočlanog
skupa
može dovesti do jednočlanog
skupa 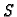 kao u primjeru 1.32, slučaj
kao u primjeru 1.32, slučaj 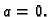 To se ne
može dogoditi zbog sljedećeg razloga. Da je doista tako, onda bi
funkcija
To se ne
može dogoditi zbog sljedećeg razloga. Da je doista tako, onda bi
funkcija 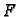 imala u točki
imala u točki 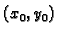 lokalni ekstrem, pa bi, zbog
neprekidne derivabilnosti funkcije
lokalni ekstrem, pa bi, zbog
neprekidne derivabilnosti funkcije 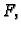 u toj točki parcijalne
derivacije od
u toj točki parcijalne
derivacije od 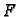 po
po 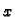 i po
i po 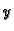 morale iščezavati, što se u
uvjetima teorema isključuje (pogledajte 1.6.1).
morale iščezavati, što se u
uvjetima teorema isključuje (pogledajte 1.6.1).
Kažemo da je funkcija 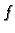 implicitno zadana jednadžbom
implicitno zadana jednadžbom 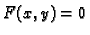 i zahtjevom
i zahtjevom
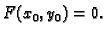 Postojanje takve funkcije nije jednostavno
dokazati, ali zato formula za derivaciju izlazi ovako.
Postojanje takve funkcije nije jednostavno
dokazati, ali zato formula za derivaciju izlazi ovako.
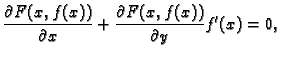 |
(1.2) |
Ovdje se zapravo 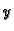 pojavljuje kao funkcija
pojavljuje kao funkcija 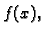 pa se često piše
pa se često piše
Primjer 1.33
Naći tangentu na graf implicitno zadane funkcije
u točki
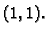
Rješenje. Imamo
Prema tome uvjeti teorema su ispunjeni. Nadalje
pa je
Dakle, jednadžba tangente je
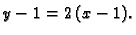
tj.
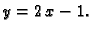
Drugu derivaciju funkcije 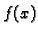 možemo izračunati derivirajući
jednadžbu 1.2 po
možemo izračunati derivirajući
jednadžbu 1.2 po 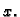
Odatle
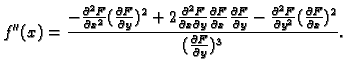 |
(1.3) |
Analogni teorem bismo mogli izreći u slučaju
U tom slučaju, uz analogne uvjete, imamo 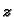 kao funkciju od
kao funkciju od 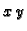 i pri tom
Tada kažemo da je funkcija
i pri tom
Tada kažemo da je funkcija 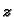 implicitno zadana jednadžbom
implicitno zadana jednadžbom
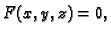 kao funkcijom od
kao funkcijom od 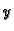 i
i 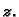
- 1.
- Kako glasi teorem srednje vrijednosti? Dokažite ga.
- 2.
- Napišite formulu konačnih prirasta. U kakvoj je ona vezi s
teoremom srednje vrijednosti?
- 3.
- Kako se definira derivacija (diferencijal) funkcije u točki?
- 4.
- Da li postojanje parcijalnih derivacija osigurava postojanje
derivacije? Navedite primjer.
- 5.
- Što se može reći o postojanju parcijalnih derivacija, ako je
funkcija derivabilna?
- 6.
- Navedite uvjete uz koje postojanje parcijalnih derivacija
povlači derivabilnost.
- 7.
- Što je tangencijalna ravnina, a što normala (na graf) funkcije u
nekoj točki? Uz koji uvjet postoje?
- 8.
- Objasnite slikom grešku koju činimo kad prirast funkcije
zamjenjujemo odgovarajućom vrijednošću diferencijala.
- 9.
- Iskažite teorem o implicitno zadanoj funkciji. Komentirajte
pretpostavke teorema.
- 10.
- Uočite na slici u prostoru osobitost točaka koje zadovoljavaju
uvjete
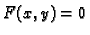 i
i
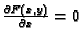 u odnosu
na one točke koje zadovoljavaju uvjete
u odnosu
na one točke koje zadovoljavaju uvjete 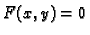 i
i
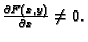
- 11.
- Izvedite formulu za drugu derivaciju funkcije implicitno zadane
jednadžbom
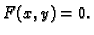
- 12.
- Izvedite formulu za treću derivaciju funkcije implicitno zadane
jednadžbom
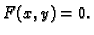
- 13.
- Kako to da postojanje parcijalnih derivacija ne osigurava
ne samo postojanje derivacije, već niti neprekidnost, kada je
parcijalna derivacija ustvari obična derivacija odgovarajuće
funkcije, i kad se ima na umu da postojanje derivacije funkcije
jedne varijable povlači njenu neprekidnost?
- 1.
- Neka je
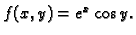 Naći
Naći 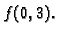
Rješenje.
- 2.
- Naći normalu na plohu
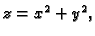 koja je paralelna s
vektorom
koja je paralelna s
vektorom
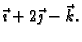
Rješenje.
Vektor normale tangencijalne ravnine
je multipl vektora smjera traženog pravca
pa su tako kanonske jednadžbe normale
- 3.
- Naći zakrivljenost funkcije implicitno zadane jednadžbom
u točki
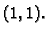
Rješenje.
Tako je, zbog 1.3,
- 4.
- Naći tangencijalnu ravninu na plohu (jednokrilni eliptički
hiperboloid) zadanu implicitno s
u točki
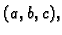 gdje je
gdje je
Rješenje. Jednadžba tangencijalne ravnine je
Uvrstimo
pomnožimo s
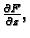 i sve prebacimo na lijevu
stranu jednadžbe. Dobivamo
To je jednadžba tangencijalne ravnine na plohu zadanu implicitno
jednadžbom
i sve prebacimo na lijevu
stranu jednadžbe. Dobivamo
To je jednadžba tangencijalne ravnine na plohu zadanu implicitno
jednadžbom
 U našem slučaju
Tako je jednadžba tangencijalne ravnine
U našem slučaju
Tako je jednadžba tangencijalne ravnine

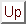



Next: Taylorov teorem srednje vrijednosti
Up: Diferencijalni račun
Previous: Derivacije funkcija više varijabli
Contents
Index
Salih Suljagic
2000-03-11
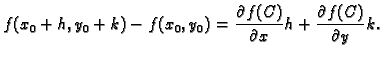
![]() Budući da je
Budući da je ![]() otvoren skup, i da spojnica
otvoren skup, i da spojnica
![]() leži u
leži u ![]() postoji
postoji
![]() takav da
točke
takav da
točke
![]() leže u
leže u ![]() za svaki
za svaki
![]() Na tom intervalu je
složena funkcija
Na tom intervalu je
složena funkcija
![]() neprekidno derivabilna, pa
ispunjava uvjete Lagrangeovog teorema srednje vrijednosti. Tako
postoji
neprekidno derivabilna, pa
ispunjava uvjete Lagrangeovog teorema srednje vrijednosti. Tako
postoji
![]() takav da vrijedi
takav da vrijedi
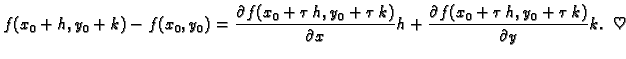
![]() u točki
u točki ![]()
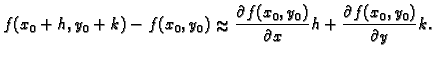
![]()
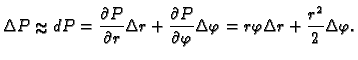
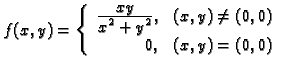
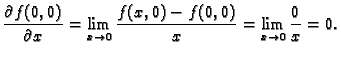
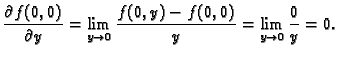
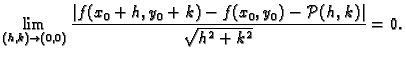
![]()
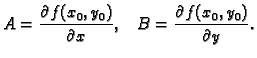
![]()
![]()
![]() U tom slučaju to je polinom 1.
stupnja od tri varijable, označavamo ga s
U tom slučaju to je polinom 1.
stupnja od tri varijable, označavamo ga s
![]() ili
ili
![]() i uz uvjet da su parcijalne derivacije
neprekidne, vrijedi
i uz uvjet da su parcijalne derivacije
neprekidne, vrijedi
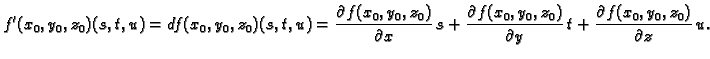
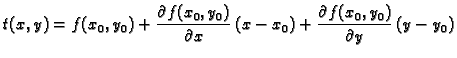
![]() okomit na tangencijalnu ravninu se zove
normala na graf funkcije
okomit na tangencijalnu ravninu se zove
normala na graf funkcije ![]() (na plohu) u točki
(na plohu) u točki
![]()
![]() u točki
u točki ![]()
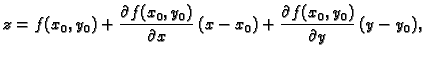
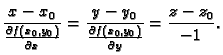
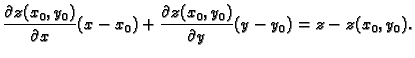
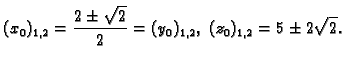
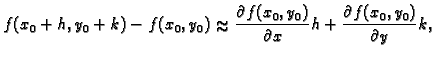
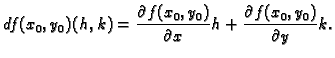
![]() U
tom slučaju imamo više rješenja, tj. ravnina
U
tom slučaju imamo više rješenja, tj. ravnina ![]() siječe plohu
siječe plohu
![]()
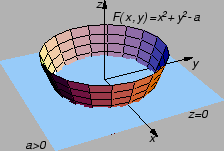
![]() imamo
imamo
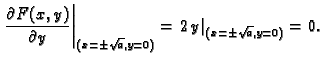
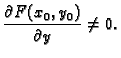
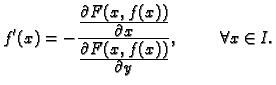
![]()
![]() takve da je
takve da je
![]() može dovesti do jednočlanog
skupa
može dovesti do jednočlanog
skupa ![]() kao u primjeru 1.32, slučaj
kao u primjeru 1.32, slučaj ![]() To se ne
može dogoditi zbog sljedećeg razloga. Da je doista tako, onda bi
funkcija
To se ne
može dogoditi zbog sljedećeg razloga. Da je doista tako, onda bi
funkcija ![]() imala u točki
imala u točki ![]() lokalni ekstrem, pa bi, zbog
neprekidne derivabilnosti funkcije
lokalni ekstrem, pa bi, zbog
neprekidne derivabilnosti funkcije ![]() u toj točki parcijalne
derivacije od
u toj točki parcijalne
derivacije od ![]() po
po ![]() i po
i po ![]() morale iščezavati, što se u
uvjetima teorema isključuje (pogledajte 1.6.1).
morale iščezavati, što se u
uvjetima teorema isključuje (pogledajte 1.6.1).
![]() implicitno zadana jednadžbom
implicitno zadana jednadžbom ![]() i zahtjevom
i zahtjevom
![]() Postojanje takve funkcije nije jednostavno
dokazati, ali zato formula za derivaciju izlazi ovako.
Postojanje takve funkcije nije jednostavno
dokazati, ali zato formula za derivaciju izlazi ovako.
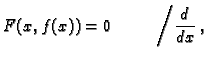
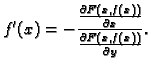
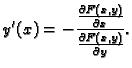
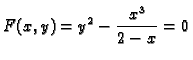
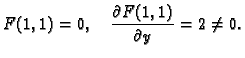
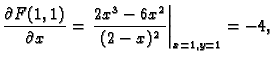
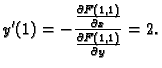
![]() možemo izračunati derivirajući
jednadžbu 1.2 po
možemo izračunati derivirajući
jednadžbu 1.2 po ![]()