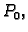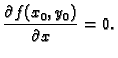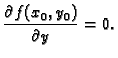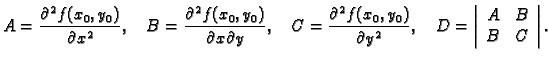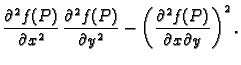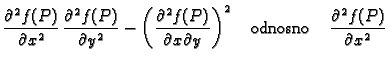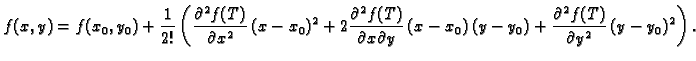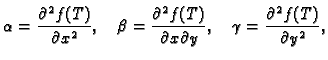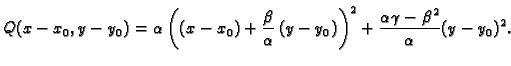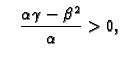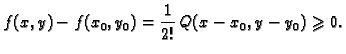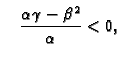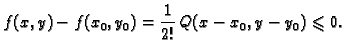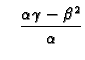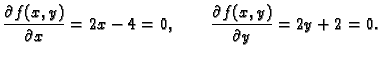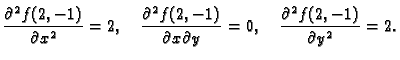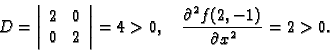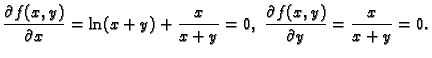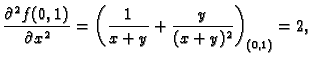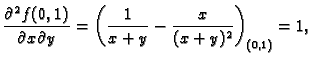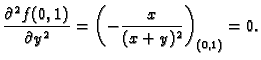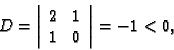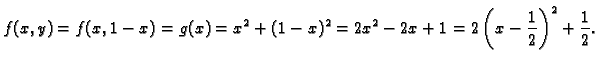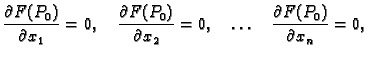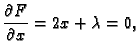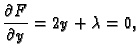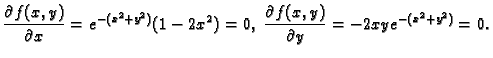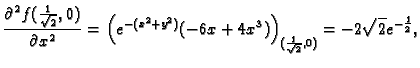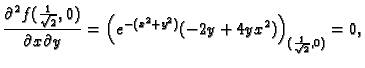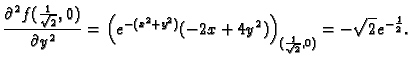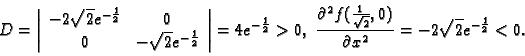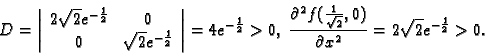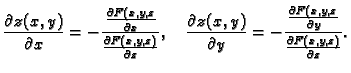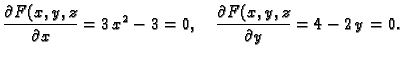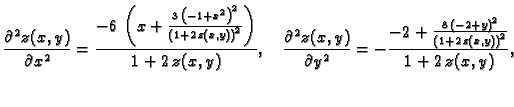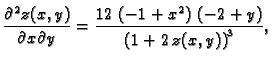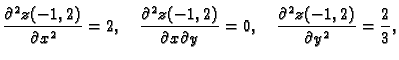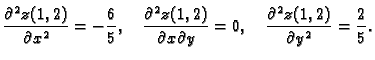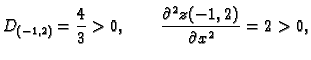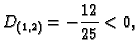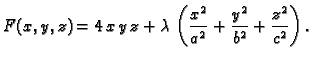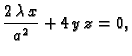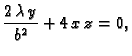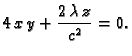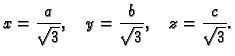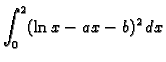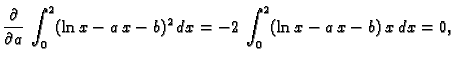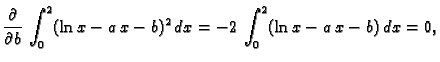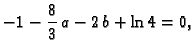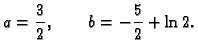Next: Višestruki integrali
Up: Diferencijalni račun
Previous: Taylorov teorem srednje vrijednosti
Contents
Index
Subsections
Ekstremi funkcija više varijabli
Da bi se naglasilo da se vrijednost funkcije u točki  upoređuje
s vrijednostima funkcije na cijeloj domeni, često se kaže apsolutni
(globalni) ekstrem.
upoređuje
s vrijednostima funkcije na cijeloj domeni, često se kaže apsolutni
(globalni) ekstrem.
Ispitivanje funkcije na ekstreme u pravilu ovisi o svojstvima
funkcije, što otežava ispitivanje. Osim toga često je za primjenu
važnije ispitati funkciju na ekstremalno ponašanje u nekoj okolini
odabrane točke. Zato ćemo radije prodiskutirati lokalne ekstreme
funkcije, koji u nekim slučajevima daju apsolutni ekstrem, a osim
toga, uz određene uvjete na derivabilnost funkcije, metoda ne ovisi
bitno o funkciji.
Lokalni ekstremi funkcija više varijabli
Definicija 15
Neka je zadana funkcija
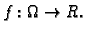
Kažemo
da

ima u točki
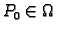
-
- lokalni maksimum, ako postoji
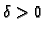 takav da
takav da
-
- strogi lokalni maksimum, ako
postoji
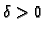 takav da
takav da
-
- lokalni minimum, ako postoji
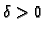 takav da
takav da
-
- strogi lokalni minimum, ako postoji
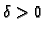 takav da
takav da
-
- lokalni ekstrem, ako u toj točki ima
lokalni maksimum ili lokalni minimum;
-
- strogi lokalni ekstrem, ako u toj točki
ima strogi lokalni maksimum ili strogi lokalni minimum.
Neka je 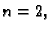 neka je
neka je  klase
klase 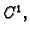 i neka ima lokalni ekstrem u
točki
i neka ima lokalni ekstrem u
točki
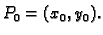 Funkcija
Funkcija
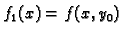 kao funkcija jedne
varijable također ima lokalni ekstrem u točki
kao funkcija jedne
varijable također ima lokalni ekstrem u točki 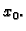 Po Fermatovoj
lemi nužno mora biti
Po Fermatovoj
lemi nužno mora biti
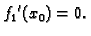 No
No
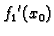 je ustvari
parcijalna derivacija od
je ustvari
parcijalna derivacija od  po
po  u točki
u točki 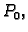 pa prema tome mora
biti
pa prema tome mora
biti
Na sličan način bismo mogli zaključiti da mora biti također
Imamo dakle ovaj zaključak. Da bi funkcija, koja ima neprekidne
parcijalne derivacije, imala lokalni ekstrem u točki 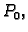 nužno je
de se njezine parcijalne derivacije poništavaju u točki
nužno je
de se njezine parcijalne derivacije poništavaju u točki 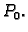
Točka
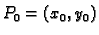 u kojoj su prve parcijalne derivacije od
u kojoj su prve parcijalne derivacije od  jednake nuli zove se stacionarna točka funkcije
jednake nuli zove se stacionarna točka funkcije 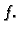 Ako je funkcija barem klase
Ako je funkcija barem klase
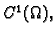 onda ona može imati
lokalni ekstrem samo u stacionarnim točkama. Nije, međutim, u svakoj
stacionarnoj točki lokalni ekstrem. Dajmo sada jedan dovoljan uvjet.
onda ona može imati
lokalni ekstrem samo u stacionarnim točkama. Nije, međutim, u svakoj
stacionarnoj točki lokalni ekstrem. Dajmo sada jedan dovoljan uvjet.
Neka je funkcija  klase
klase 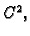 i neka je
i neka je
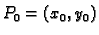 stacionarna točka funkcije
stacionarna točka funkcije 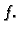 Stavimo
Stavimo
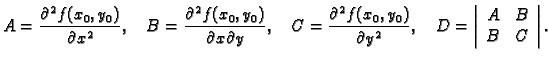 |
(1.6) |
- 1.
- Ako je
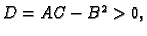 onda
onda  ima lokalni ekstrem u točki
ima lokalni ekstrem u točki
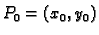 i to lokalni minimum, ako je
i to lokalni minimum, ako je 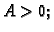 odnosno lokalni
maksimum, ako je
odnosno lokalni
maksimum, ako je 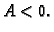
- 2.
- Ako je
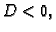 onda
onda  nema lokalni ekstrem u točki
nema lokalni ekstrem u točki
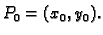
- 3.
- Ako je
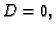 onda na temelju drugih parcijalnih derivacija ne
možemo zaključiti ništa o ponašanju funkcije u okolini točke
onda na temelju drugih parcijalnih derivacija ne
možemo zaključiti ništa o ponašanju funkcije u okolini točke
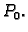
Ovaj dovoljan kriterij se može objasniti pomoću Taylorove formule.
Neka je
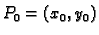 stacionarna točka funkcije
stacionarna točka funkcije 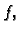 i neka su
i neka su
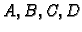 definirani kao u (1.6). Pretpostavimo je
definirani kao u (1.6). Pretpostavimo je 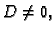 i da je
i da je 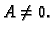 Druge parcijalne derivacije funkcije
Druge parcijalne derivacije funkcije  su
neprekidne, pa je neprekidna i funkcija
su
neprekidne, pa je neprekidna i funkcija
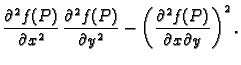 |
(1.7) |
Pema tome postoji (teorem 1) 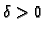 takav, da za
svaki
takav, da za
svaki
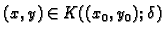 funkcija
funkcija
ima isti znak kao 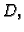 odnosno
odnosno 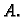 Po Taylorovom teoremu, za
svaki
Po Taylorovom teoremu, za
svaki
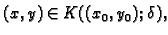 postoji točka
postoji točka
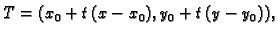
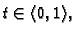 na
spojnici točaka
na
spojnici točaka 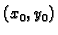 i
i 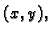 takva da je
Stavimo
Tada
takva da je
Stavimo
Tada 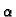 ima isti znak kao
ima isti znak kao 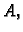 i
i
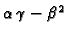 ima isti znak kao
ima isti znak kao 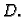 Imamo nadalje
Znak funkcije
Imamo nadalje
Znak funkcije 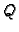 ovisi samo o
ovisi samo o 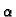 i
i
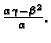
1. a) Ako je 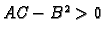 i
i 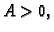 onda je
onda je
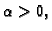
i
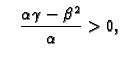
za
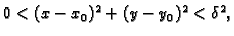 pa je
Prema tome u točki
pa je
Prema tome u točki  funkcija ima lokalni minimum.
funkcija ima lokalni minimum.
1. b) Ako je 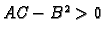 i
i 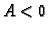 onda je
onda je
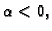
i
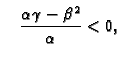
pa je
Prema tome u točki  funkcija ima lokalni maksimum.
funkcija ima lokalni maksimum.
2. Ako je 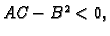 onda je
onda je
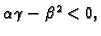 pa bez obzira
kakav znak imao
pa bez obzira
kakav znak imao 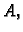 odnosno
odnosno 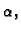 sumandi u
sumandi u
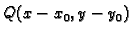 imaju
različiti znak, jer su
imaju
različiti znak, jer su
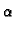
i
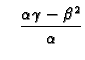
suprotnih znakova. To znači da
je
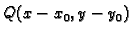 po nekim smjerovima pozitivan, a po nekim drugim
smjerovima negativan. U tom slučaju funkcija u točki
po nekim smjerovima pozitivan, a po nekim drugim
smjerovima negativan. U tom slučaju funkcija u točki  nema
lokalni ekstrem.
nema
lokalni ekstrem.
3. Ako je 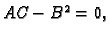 onda ne možemo ništa reći o predznaku
onda ne možemo ništa reći o predznaku
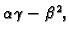 pa u tom slučaju ne možemo ništa
zaključiti o ponašanju funkcije u točki
pa u tom slučaju ne možemo ništa
zaključiti o ponašanju funkcije u točki  samo na temelju
drugih parcijalnih derivacija.
samo na temelju
drugih parcijalnih derivacija.
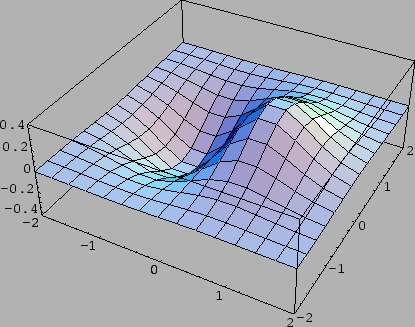
Primjer 1.39
Naći lokalne ekstreme funkcije
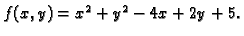
Rješenje.
Stacionarna točka je
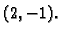
Prema tome funkcija ima u
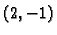
lokalni minimum
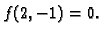
Primjer 1.40
Naći lokalne ekstreme funkcije
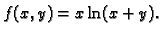
Rješenje.
Stacionarna točka je
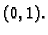
pa funkcija nema lokalnih ekstrema.
Uvjetni ekstremi
Primjer 1.41
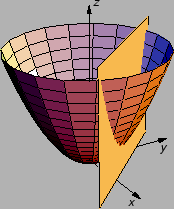
Neka je
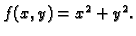
Ova funkcija očito ima lokalni (i
apsolutni) minimum u ishodištu. No ako promatramo samo one točke u domeni,
koje zadovoljavaju uvjet
onda to znači da siječemo plohu ravninom paralelnom osi
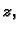
čija je
jednadžba
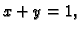
i tako dobivamo krivulju, koja može imati lokalne
ekstreme u točkama koje nisu stacionarne za
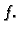
U ovom primjeru
Dobili smo funkciju jedne
varijable, čije ekstreme možemo ispitati pomoću diferencijalnog
računa. No u ovom primjeru i bez diferencijalnog računa vidimo da
funkcija ima lokalni minimum u točki
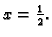
Drugim
riječima funkcija
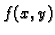
ima, uz uvjet
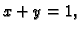
lokalni minimum u
točki
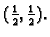
Definicija 16
Neka je

područje u
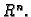
Kažemo da funkcija
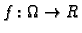
ima
uvjetni ekstrem u točki
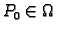
uz uvjete
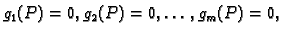
ako funkcija
gdje je
ima lokalni ekstrem u točki
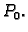
Gornji primjer pokazuje kako možemo rješavati takve probleme. Koristeći
uvjete, smanjimo broj varijabli u funkciji 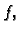 i onda rješavamo problem
običnog lokalnog ekstrema za tako dobivenu funkciju.
i onda rješavamo problem
običnog lokalnog ekstrema za tako dobivenu funkciju.
Postoji i druga metoda metoda Lagrangeovih
multiplikatora, koja
je u nekim slučajevima jednostavnija. Ta metoda se sastoji u
sljedećem. Formiramo novu funkciju
Ako je  klase
klase
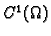 i u točki
i u točki  ima uvjetni ekstrem, uz
uvjete
onda se funkcije
ima uvjetni ekstrem, uz
uvjete
onda se funkcije
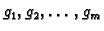 i parcijalne derivacije od
i parcijalne derivacije od 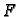 poništavaju u točki
poništavaju u točki 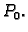
Dakle, nužan uvjet da funkcija  ima uvjetni ekstrem u točki
ima uvjetni ekstrem u točki  je da
je da  zadovoljava sljedeće
zadovoljava sljedeće
Ovo
je sustav od 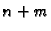 jednadžbi za
jednadžbi za 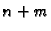 nepoznanica
nepoznanica
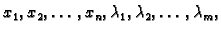 pomoću
kojeg nađemo točke
pomoću
kojeg nađemo točke
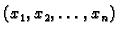 u kojima funkcija možda
ima uvjetne ekstreme.
u kojima funkcija možda
ima uvjetne ekstreme.
Primjer 1.42
Izradimo na ovaj način gornji primjer.
Ovo je sustav iz kojeg lako izračunamo
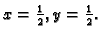
Iz
same prirode problema (geometrijska interpretacija), slijedi da je u točki
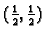
uvjetni minimum funkcije
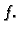
Ova metoda daje samo stacionarne točke. U nekim slučajevima priroda
problema (geometrijska ili fizikalna) odlučuje o tome da li je u
stacionarnoj točki doista uvjetni ekstrem ili ne. U gornjem primjeru
je upravo to slučaj. Graf funkcije je rotacioni paraboloid, i jasno
je da funkcija ima u stacionarnoj točki lokalni minimum.
- 1.
- Što je to apsolutni ekstrem?
- 2.
- Kad kažemo da funkcija ima u nekoj točki lokalni ekstrem? Zašto
pridjev lokalni? Kakvih lokalnih ekstrema ima?
- 3.
- Koji je nužan uvjet da derivabilna funkcija u nekoj točki ima
lokalni ekstrem?
- 4.
- Kad neku točku zovemo stacionarnom točkom funkcije
 ? Da li u
stacionarnoj točki funkcija nužno ima lokalni ekstrem?
? Da li u
stacionarnoj točki funkcija nužno ima lokalni ekstrem?
- 5.
- Objasnite postupak kojim nalazimo lokalne ekstreme funkcije od
dvije varijable.
- 6.
- Da li se u nužnom uvjetu 1.6.1
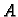 može zamijeniti
s
može zamijeniti
s 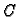 ?
?
- 7.
- Zašto nismo pod 1. u 1.6.1 razmatrali slučaj
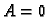 ?
?
- 8.
- Koje se važno svojstvo neprekidnih funkcija koristi u
objašnjenju dovoljnog uvjeta za postojanje ekstrema?
- 9.
- Definirajte uvjetni ekstrem.
- 10.
- Objasnite metodu Lagrangeovih multiplikatora.
- 1.
- Naći lokalne ekstreme funkcije
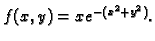
Rješenje. Stacionarne točke su
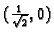 i
i
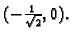
Razmotrimo najprije točku
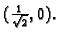 Dakle u
Dakle u
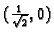 funkcija ima lokalni maksimum i to
funkcija ima lokalni maksimum i to
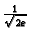 . Lako se vidi da za drugu stacionarnu točku imamo
Dakle u
. Lako se vidi da za drugu stacionarnu točku imamo
Dakle u
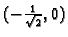 funkcija ima lokalni minimum i to
funkcija ima lokalni minimum i to
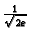 .
.
- 2.
- Naći ekstreme funkcije
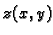 implicitno zadane formulom
implicitno zadane formulom
Rješenje. Stavimo
Za 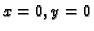 imamo
imamo
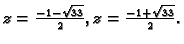 Tako postoji točka s pozitivnom
aplikatom u kojoj se poništava funkcija
Tako postoji točka s pozitivnom
aplikatom u kojoj se poništava funkcija 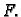 Zatim parcijalna
derivacija od
Zatim parcijalna
derivacija od 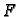 po
po 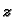 se poništava samo u točkama u kojima je
se poništava samo u točkama u kojima je
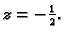 Uvjet u zadatku već isključuje tu točku. Dakle,
postoji implicitno zadana funkcija
Uvjet u zadatku već isključuje tu točku. Dakle,
postoji implicitno zadana funkcija 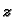 kao funkcija od
kao funkcija od  i
i 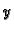 takva, da je
Odatle slijedi da je nužan uvjet za ekstrem
Stacionarne točke su prema tome
takva, da je
Odatle slijedi da je nužan uvjet za ekstrem
Stacionarne točke su prema tome
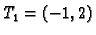 i
i
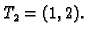 Pripadne
vrijednosti za
Pripadne
vrijednosti za 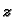 jesu
jesu 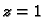 i
i 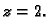
Druge derivacije su
pa je
Odatle
pa u točki 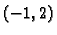 imamo minimum, i to
imamo minimum, i to
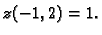 Zatim
pa u točki
Zatim
pa u točki 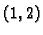 nemamo ekstrem.
nemamo ekstrem.
- 3.
- Tavan kuće ima oblik gornje polovine elipsoida, čije su
poluosi
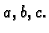 Na tavanu se želi izgraditi stambeni prostor
u obliku kvadra. Kolike trebaju biti njegove dimenzije, ako se želi dobiti
maksimalni volumen?
Na tavanu se želi izgraditi stambeni prostor
u obliku kvadra. Kolike trebaju biti njegove dimenzije, ako se želi dobiti
maksimalni volumen?
Rješenje. Ako je 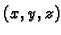 točka u prvom oktantu u kojoj kvadar dotiče
elipsoid, onda je volumen kvadra
točka u prvom oktantu u kojoj kvadar dotiče
elipsoid, onda je volumen kvadra
Prema tome treba naći maksimum funkcije 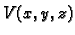 uz uvjet
uz uvjet
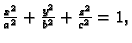 s tim da je
s tim da je
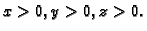 Lagrangeova funkcija je
Ako parcijalne derivacije od
Lagrangeova funkcija je
Ako parcijalne derivacije od 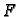 izjednačimo s nulom, dobivamo sustav
jednadžbi
Pomnožimo prvu jednadžbu s
izjednačimo s nulom, dobivamo sustav
jednadžbi
Pomnožimo prvu jednadžbu s 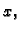 drugu s
drugu s 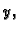 treću sa
treću sa 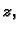 i
uvrstimo u jednadžbu elipsoida. Dobivamo
i
uvrstimo u jednadžbu elipsoida. Dobivamo
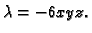 Uvrstimo
taj
Uvrstimo
taj 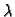 u gornje jednadžbe. Dobivamo
Iz geometrije problema je jasno da su to vrijednosti uz koje se
postiže maksimalni volumen.
u gornje jednadžbe. Dobivamo
Iz geometrije problema je jasno da su to vrijednosti uz koje se
postiže maksimalni volumen.
- 4.
- Odrediti
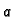 i
i 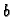 tako da
ima minimalnu vrijednost.
tako da
ima minimalnu vrijednost.
Rješenje. Budući da integral predstavlja površinu ispod grafa funkcije
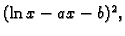 jasno je da ne postoji maksimum. S druge strane za
bilo koje vrijednosti
jasno je da ne postoji maksimum. S druge strane za
bilo koje vrijednosti 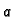 i
i 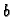 integral prima nenegativne
vrijednosti. Odatle je jasno da u stacionarnoj točki imamo minimum.
integral prima nenegativne
vrijednosti. Odatle je jasno da u stacionarnoj točki imamo minimum.
Rješenje ovog sustava je
- 5.
- Naći točku na plohi
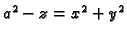 u kojoj treba postaviti
tangencijalnu ravninu u prvom oktantu tako da volumen tetraedra što ga ta
ravnina zatvara s koordinatnim ravninama bude minimalan.
u kojoj treba postaviti
tangencijalnu ravninu u prvom oktantu tako da volumen tetraedra što ga ta
ravnina zatvara s koordinatnim ravninama bude minimalan.
Rješenje. Neka je tražena točka
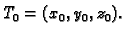 Budući da leži na
plohi, mora biti
Budući da leži na
plohi, mora biti
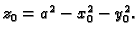 Jednadžba tangencijalne ravnine
na plohu u toj točki je
Jednadžba tangencijalne ravnine
na plohu u toj točki je
Odsječci tangencijalne ravnine na osima su redom
Prema tome, volumen tetraedra je
Ako parcijalne derivacije po 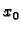 i
i 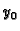 izjednačimo s nulom,
dobivamo
Rješenje je
Dakle, tangencijalna ravnina na plohu
izjednačimo s nulom,
dobivamo
Rješenje je
Dakle, tangencijalna ravnina na plohu
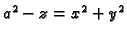 u točki
u točki
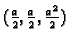 određuje s koordinatnim
ravninama tetraedar najmanjeg volumena.
određuje s koordinatnim
ravninama tetraedar najmanjeg volumena.





Next: Višestruki integrali
Up: Diferencijalni račun
Previous: Taylorov teorem srednje vrijednosti
Contents
Index
Salih Suljagic
2000-03-11
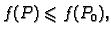 za svaki
za svaki
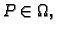
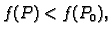 za svaki
za svaki
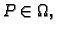 različit od
različit od 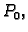
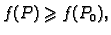 za svaki
za svaki
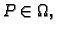
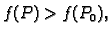 za svaki
za svaki
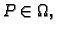 različit od
različit od