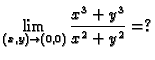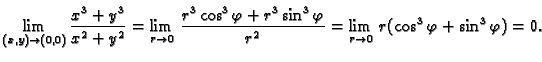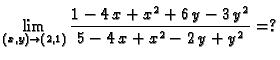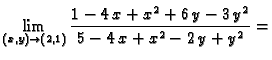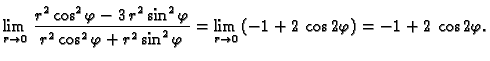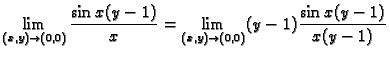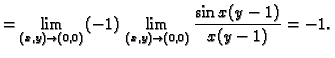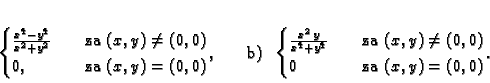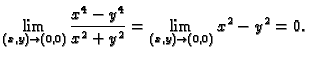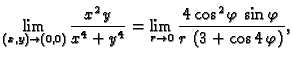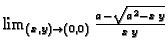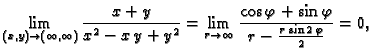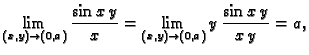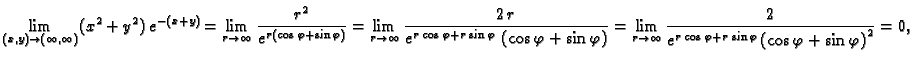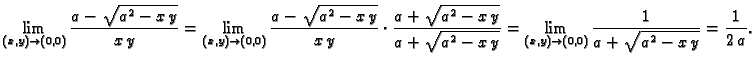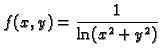Next: Derivacije funkcija više varijabli
Up: Diferencijalni račun
Previous: Funkcije više varijabli
Contents
Index
Subsections
Definicija 7
Neka je

područje u
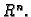
Kažemo da je
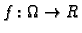 neprekidna u točki
neprekidna u točki
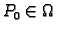
,
ako za svaki
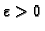
postoji
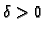
tako da
Ako

nije neprekidna u točki
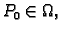
onda kažemo da
 ima prekid u
ima prekid u 
.
Ako je  neprekidna u svakoj točki nekog skupa
neprekidna u svakoj točki nekog skupa 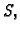 onda kažemo da
je
onda kažemo da
je  neprekidna na skupu
neprekidna na skupu 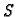 .
.
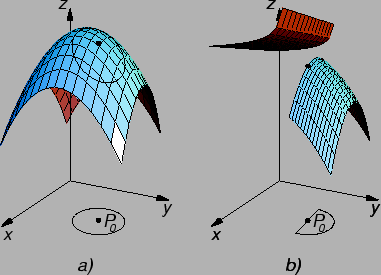
Na sljedećim slikama se vidi tipično ponašanje funkcije u okolini
točke neprekidnosti, i točke prekida. Svjetlo osjenčani skup u
ravnini 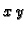 je ortogonalna projekcija onog dijela grafa funkcije
je ortogonalna projekcija onog dijela grafa funkcije
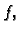 koji se nalazi između ravnina
koji se nalazi između ravnina
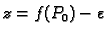 i
i
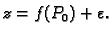 Dakle, ako je
Dakle, ako je 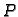 iz tog skupa, onda vrijedi
iz tog skupa, onda vrijedi
odnosno
Na slici 1.9 tamnije
osjenčani skup je krug radiusa 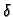 oko točke
oko točke 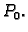 Na lijevom
dijelu slike se vidi da se za odabrani
Na lijevom
dijelu slike se vidi da se za odabrani
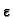 može naći
može naći
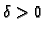 takav da krug oko
takav da krug oko  s tim radiusom leži u svjetlije
osjenčanom skupu. S druge strane, na desnom dijelu slike nije moguće
naći takav
s tim radiusom leži u svjetlije
osjenčanom skupu. S druge strane, na desnom dijelu slike nije moguće
naći takav 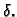 Ma kako malen krug izabrali, uvijek ima točaka
u njemu koje su izvan svjetlije osjenčanog skupa. U tim točkama
vrijednost funkcije se više ne nalazi između ravnina. Pri tom valja
naglasiti da se to događa za svaki
Ma kako malen krug izabrali, uvijek ima točaka
u njemu koje su izvan svjetlije osjenčanog skupa. U tim točkama
vrijednost funkcije se više ne nalazi između ravnina. Pri tom valja
naglasiti da se to događa za svaki
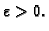
Slika 1.9:
Ponašanje funkcije u okolini točke neprekidnosti i točke prekida.
|
|
Primjer 1.11
Funkcija
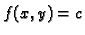
je neprekidna u svakoj točki u
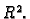
Rješenje. Neka je
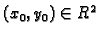 proizvoljna točka, i neka je
proizvoljna točka, i neka je
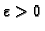 proizvoljan.
proizvoljan.
Ova nejednakost je ispunjena za svaki
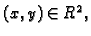
pa za
bilo koji
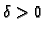
vrijedi
Tako je

neprekidna u točki
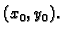
Budući da je točka
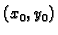
uzeta proizvoljno,
slijedi da je

neprekidna u svakoj točki.
Primjer 1.12
Funkcija
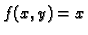
je neprekidna u svakoj točki u
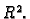
Rješenje. Neka je
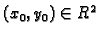 proizvoljna točka, i
neka je
proizvoljna točka, i
neka je
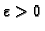 proizvoljan.
proizvoljan.
Uzmimo
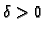
tako
da je
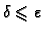
(sl.
1.10) Tada
iz
slijedi
Tako je

neprekidna u točki
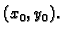
Kako je
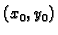
izabrana proizvoljno, slijedi da je

neprekidna u svakoj točki.
Slika 1.10:
Mogući 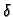 za izabrani
za izabrani
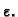
|
|
Primjer 1.13
Funkcija
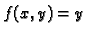
je neprekidna u svakoj točki u
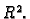
Rješenje. Neka je
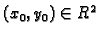 proizvoljna točka, i
neka je
proizvoljna točka, i
neka je
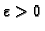 proizvoljan.
proizvoljan.
Dakle za svaki
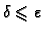
vrijedi
Tako je

neprekidna u točki
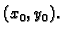
Budući da je ta točka
proizvoljna, slijedi da je

neprekidna u svakoj točki.
Dokaz.

Slika 1.11:
a) Neprekidna funkcija je lokalno ograničena. b) U okolini točke prekida funkcija ne mora biti ograničena.
|
|
Na slici 1.11 se lijevo nalazi graf neprekidne
funkcije, a desno graf funkcije koja ima prekid u točkama za koje je
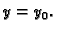 Pri tom je taj prekid takav da
Pri tom je taj prekid takav da
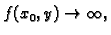 kad
kad
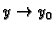 preko vrijednosti manjih od
preko vrijednosti manjih od 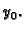 To znači da ne
postoji krug
To znači da ne
postoji krug 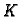 oko točke
oko točke  takav da bude
takav da bude
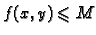 za
svaki
za
svaki
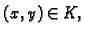 ma kako veliki
ma kako veliki 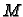 uzeli.
uzeli.
Dokaz. Dokažimo drugu tvrdnju i to za zbroj.
Za proizvoljan
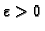 postoje
postoje
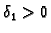 i
i
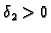 takvi da vrijedi
takvi da vrijedi
i
Ako za 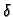 uzmemo manji od brojeva
uzmemo manji od brojeva
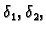 tj.
tj.
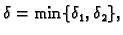 onda vrijedi
onda vrijedi

Teorem 3
Neka je
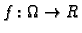
neprekidna u točki
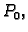
neka
je
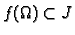
i neka je
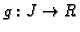
neprekidna u
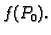
Tada je funkcija
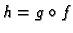
neprekidna u
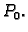
Slika 1.12:
Kompozicija funkcija.
|
|
Dokaz.

Primjer 1.14
Funkcija
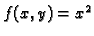
je neprekidna u svakoj točki u
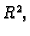
jer je produkt dvije svuda neprekidne funkcije.
Funkcija
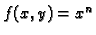 je neprekidna u svakoj točki u
je neprekidna u svakoj točki u 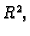 jer je produkt neprekidnih funkcija.
jer je produkt neprekidnih funkcija.
Polinom od dvije ili više varijabli je neprekidna funkcija svuda.
Racionalna funkcija je neprekidna svuda gdje je definirana, tj. svuda
osim u nultočkama nazivnika.
Kompozicije elementarnih funkcija i polinoma ili racionalnih funkcija
od više varijabli jesu neprekidne funkcije svuda gdje su
definirane.Tako na pr.
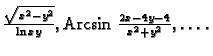 su neprekidne funkcije
na svojim domenama.
su neprekidne funkcije
na svojim domenama.
Definicija 8
Neka je funkcija

definirana na području
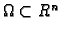
osim možda u
točki
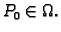
Kažemo da
 ima limes L u točki
ima limes L u točki

ako za svaki
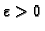
postoji
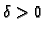
tako da
Pišemo
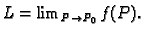
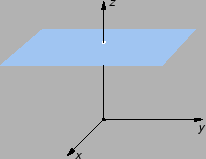
Kao što pokazuje sljedeća slika, funkcija može biti definirana u
točki 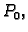 i da ima limes u
i da ima limes u  koji nije jednak vrijednosti
funkcije u točki
koji nije jednak vrijednosti
funkcije u točki 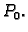 Na slici je graf funkcije
Na slici je graf funkcije
Ta funkcija ima vrijednost 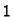 u
svakoj točki osim u ishodištu, gdje je njezina vrijednost
u
svakoj točki osim u ishodištu, gdje je njezina vrijednost 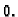 Iz
definicije slijedi da limes u ishodištu postoji i da je jednak
Iz
definicije slijedi da limes u ishodištu postoji i da je jednak 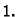
Dokaz. 1. Ako je  neprekidna u točki
neprekidna u točki 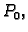 onda
onda
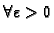 postoji
postoji 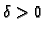 tako da
tako da
pa pogotovo
Odatle slijedi da  ima limes u točki
ima limes u točki  i
i
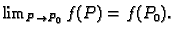
ii) Neka  ima limes u točki
ima limes u točki  i neka je
i neka je
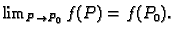 To znači da
To znači da
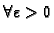 postoji
postoji 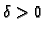 tako da
tako da
Specijalno za
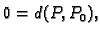 tj. za
tj. za 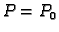 je
je
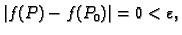 pa slijedi
tj. funkcija je neprekidna u točki
pa slijedi
tj. funkcija je neprekidna u točki 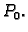

Primjer 1.15
Tako na pr.
jer je ova funkcija neprekidna u točki
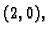
pa se limes nalazi
jednostavnim uvrštavanjem.
Ako postoji
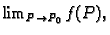 onda je on jedinstven.
onda je on jedinstven.
Neka funkcije  i
i 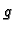 imaju limese u točki
imaju limese u točki 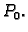 Tada
Tada
- 1.
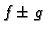 ima limes u točki
ima limes u točki  i
i
- 2.
- za
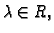
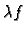 ima limes u točki
ima limes u točki  i
i
- 3.
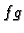 ima limes u točki
ima limes u točki  i
i
- 4.
- Uz dodatni uvjet
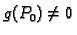 i
i
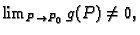
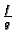 ima limes u točki
ima limes u točki  i
i
Primjer 1.16
Rješenje. Zaista, iz
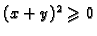 slijedi
slijedi
Slično iz
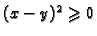
slijedi
Tako je
i odatle je jasno da gornji limes postoji i da je jednak
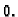
Primjer 1.17
ne postoji.
Rješenje. Premda je
i
ipak, ako stavimo
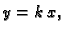
onda
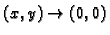
čim
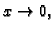
i tada je
Za različite
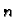
dobivamo različite limese, što znači da
zapravo ne postoji.
Dapače, može se dogoditi da limesi po svim pravcima postoje i da su
jednaki, a da limes ipak ne postoji, kao što pokazuje sljedeći
primjer.
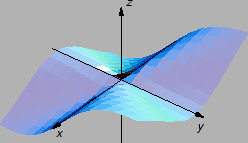
Primjer 1.18
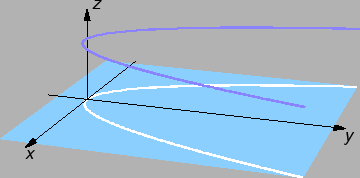
Neka je
Graf te funkcije je dan na sljedećoj slici
Tada po svakom pravcu kroz ishodište limes u
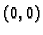
je jednak
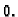
Ipak, ako se ishodištu približavamo po krivulji
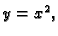
onda je
vrijednost funkcije stalno jednaka
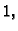
pa je i limes jednak
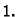
Ovi primjeri pokazuju da traženje limesa funkcije više varijabli
nije lagan posao, i da se ne smije na osnovi postojanja sukcesivnih
limesa ili limesa po određenim putevima, bez dodatnih informacija
ništa zaključivati. Ipak, imamo jednu jednostavnu metodu kojom u
nekim slučajevima možemo naći limes funkcije od dvije
varijable. Ideja se sastoji u tome da točku u kojoj se traži limes
shvatimo kao pol polarnog koordinatnog sustava u ravnini. Nakon
zamjene koordinata dovoljno je zahtijevati da 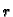 teži k
teži k 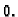
Primjer 1.20
Rješenje. Stavimo
Za različite
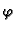
dobivamo različite rezultate. Dakle limes ne
postoji.
Dakako, možemo koristiti poznate limese funkcija jedne varijable.
- 1.
- Definirajte neprekidnost funkcije više varijabli u točki.
- 2.
- Što znači kad kažemo da je funkcija neprekidna na skupu, a što kad
se kaže da ima prekid na skupu?
- 3.
- Koja su svojstva funkcija neprekidnih u točki?
- 4.
- Što se može reći o neprekidnosti elementarnih
funkcija više varijabli?
- 5.
- Definirajte limes funkcije više
varijabli u točki.
- 6.
- Koja svojstva ima limes?
- 7.
- Iskažite teorem
koji govori o vezi između neprekidnosti i limesa.
- 8.
- Da li se limes
može računati tako da se sukcesivno računaju limesi po pojedinim
varijablama?
- 1.
- Ispitajte da li su sljedeće funkcije neprekidne u točki
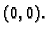
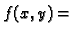
a)
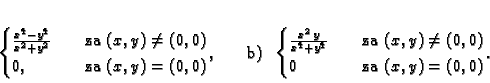
Rješenje. a) Očito je
b) Ako pređemo na polarni sustav,
pa nepostoji limes, jer  teži u beskonačnost po gotovo svim
putevima u ishodište. Nađite puteve u ishodište po kojima postoje
konačni limesi.
teži u beskonačnost po gotovo svim
putevima u ishodište. Nađite puteve u ishodište po kojima postoje
konačni limesi.
- 2.
- Nađite sljedeće limese, ako postoje
- (a)
-
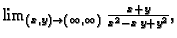
- (b)
-
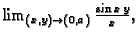
- (c)
-
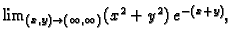
- (d)
-
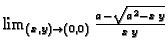
Rješenje. a)
b)
c)
d)
- 3.
- Da li je moguće definirati funkciju
u
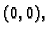 tako da dobivena funkcija bude neprekidna.
tako da dobivena funkcija bude neprekidna.
Rješenje. Imamo
Ako stavimo
onda je 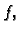 prema teoremu 4, neprekidna u
prema teoremu 4, neprekidna u 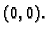





Next: Derivacije funkcija više varijabli
Up: Diferencijalni račun
Previous: Funkcije više varijabli
Contents
Index
Salih Suljagic
2000-03-11
![]() neprekidna u svakoj točki nekog skupa
neprekidna u svakoj točki nekog skupa ![]() onda kažemo da
je
onda kažemo da
je ![]() neprekidna na skupu
neprekidna na skupu ![]() .
.![]() neprekidna u svakoj točki nekog skupa
neprekidna u svakoj točki nekog skupa ![]() onda kažemo da
je
onda kažemo da
je ![]() neprekidna na skupu
neprekidna na skupu ![]() .
.![]() je ortogonalna projekcija onog dijela grafa funkcije
je ortogonalna projekcija onog dijela grafa funkcije
![]() koji se nalazi između ravnina
koji se nalazi između ravnina
![]() i
i
![]() Dakle, ako je
Dakle, ako je ![]() iz tog skupa, onda vrijedi
iz tog skupa, onda vrijedi
![]() proizvoljna točka, i neka je
proizvoljna točka, i neka je
![]() proizvoljan.
proizvoljan.
![]() proizvoljna točka, i
neka je
proizvoljna točka, i
neka je
![]() proizvoljan.
proizvoljan.
![]() proizvoljna točka, i
neka je
proizvoljna točka, i
neka je
![]() proizvoljan.
proizvoljan.
![]()
![]() postoje
postoje
![]() i
i
![]() takvi da vrijedi
takvi da vrijedi
![]()
![]() je neprekidna u svakoj točki u
je neprekidna u svakoj točki u ![]() jer je produkt neprekidnih funkcija.
jer je produkt neprekidnih funkcija.
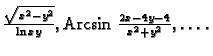 su neprekidne funkcije
na svojim domenama.
su neprekidne funkcije
na svojim domenama.![]() i da ima limes u
i da ima limes u ![]() koji nije jednak vrijednosti
funkcije u točki
koji nije jednak vrijednosti
funkcije u točki ![]() Na slici je graf funkcije
Na slici je graf funkcije
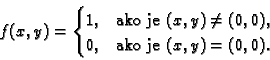
![]() ima limes u
ima limes u ![]() i neka je
i neka je
![]() Tada je
Tada je ![]() neprekidna u
neprekidna u ![]()
![]() neprekidna u točki
neprekidna u točki ![]() onda
onda
![]() postoji
postoji ![]() tako da
tako da
![]() ima limes u točki
ima limes u točki ![]() i neka je
i neka je
![]() To znači da
To znači da
![]() postoji
postoji ![]() tako da
tako da
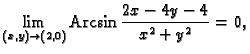
![]() onda je on jedinstven.
onda je on jedinstven.
![]() i
i ![]() imaju limese u točki
imaju limese u točki ![]() Tada
Tada
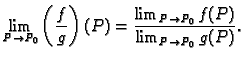
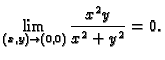
![]() slijedi
slijedi
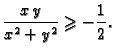
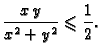
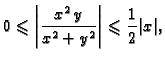
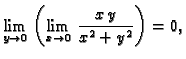
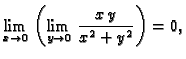
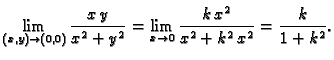
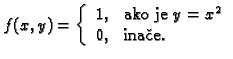
![]() teži k
teži k ![]()