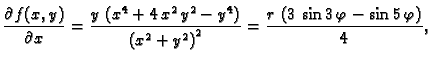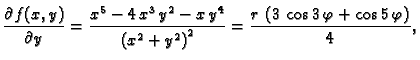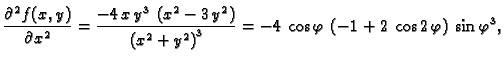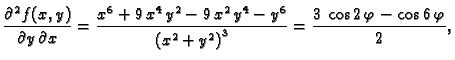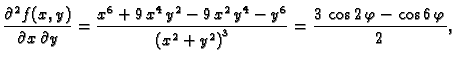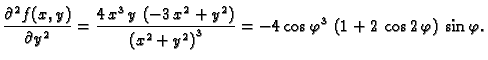Next: Teorem srednje vrijednosti
Up: Diferencijalni račun
Previous: Neprekidnost i limes
Contents
Index
Subsections
Definicija 9
Neka je

područje u
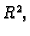
neka je
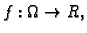
zadana funkcija, i neka je
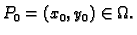
Ako postoji
onda kažemo da funkcija

ima
parcijalnu derivaciju po  u točki
u točki

i pišemo
Analogno, ako postoji
onda kažemo da funkcija

ima
parcijalnu derivaciju po 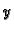 u točki
u točki

i pišemo
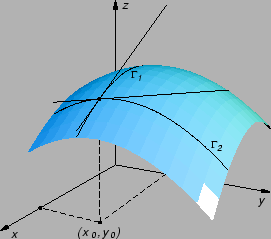
Graf 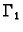 funkcije
funkcije
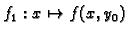 je krivulja, koja se
dobije kad se ploha
je krivulja, koja se
dobije kad se ploha 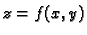 presiječe ravninom
presiječe ravninom 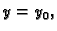 pa je tako
pa je tako
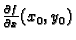 koeficijent smjera tangente
na tu krivulju u točki
koeficijent smjera tangente
na tu krivulju u točki
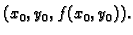
Slično, graf 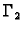 funkcije
funkcije
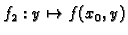 je krivulja,
koja se dobije kad se ploha
je krivulja,
koja se dobije kad se ploha 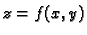 presiječe ravninom
presiječe ravninom 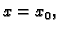 pa
je tako
pa
je tako
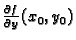 koeficijent smjera
tangente na tu krivulju u točki
koeficijent smjera
tangente na tu krivulju u točki
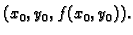
Definicija 10
Neka je

područje u
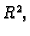
i neka je
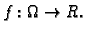
Ako

ima parcijalnu derivaciju po

u
svakoj točki iz
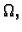
onda je definirana funkcija
Tu funkciju zovemo
parcijalnom
derivacijom funkcije  po varijabli
po varijabli
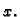
Analogno se definira parcijalna derivacija funkcije  po
po 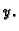
U točki 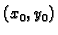 ove derivacije imaju vrijednosti
ove derivacije imaju vrijednosti
Primjer 1.23
Sada možemo
primjer
1.22 izraditi na drugi način. Tako da najprije
nađemo parcijalnu derivaciju funkcije, i da zatim supstituiramo
točku
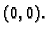
Slično
Ako imamo funkciju od tri varijable 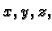 onda imamo još jednu
parcijalnu derivaciju
onda imamo još jednu
parcijalnu derivaciju
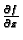 i t.d.
i t.d.
Vidimo da se parcijalna derivacija računa tako da se varijabla po
kojoj se derivira shvati kao varijabla, a ostale kao konstante. Dakle
formalno funkciju deriviramo kao da je od jedne varijable s više
parametara. To znači da vrijede pravila za deriviranje kao kod
funkcija od jedne verijable.
Parcijalna derivacija
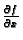 funkcije
funkcije  po
po
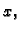 ukoliko postoji, je također funkcija od dvije varijable
ukoliko postoji, je također funkcija od dvije varijable  i
i
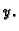 Njezina parcijalna derivacija po
Njezina parcijalna derivacija po  u točki
u točki
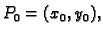 ako
postoji, je
ako
postoji, je
a parcijalna derivacija po 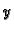 je
Te derivacije
zovemo drugom parcijalnom derivacijom od
je
Te derivacije
zovemo drugom parcijalnom derivacijom od  po
po  u
točki
u
točki  , i drugom mješovitom parcijalnom derivacijom od
, i drugom mješovitom parcijalnom derivacijom od  po
po  i po
i po 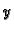 u točki
u točki  .
.
Slično, iz funkcije
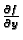 dobivamo parcijalne
derivacije
dobivamo parcijalne
derivacije
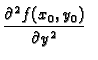
i
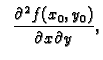
koje zovemo drugom parcijalnom derivacijom od
 po
po 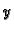 u točki
u točki  , i drugom mješovitom parcijalnom derivacijom
od
, i drugom mješovitom parcijalnom derivacijom
od  po
po 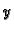 i po
i po  u točki
u točki  . Dalje imamo treće parcijalne
derivacije
i t.d. Druge
parcijalne derivacije se također zovu parcijalne derivacije drugog
reda, treće trećeg reda i t.d. Parcijalne derivacije drugog,
trećeg, ...reda se zovu parcijalne derivacije višeg
reda.
. Dalje imamo treće parcijalne
derivacije
i t.d. Druge
parcijalne derivacije se također zovu parcijalne derivacije drugog
reda, treće trećeg reda i t.d. Parcijalne derivacije drugog,
trećeg, ...reda se zovu parcijalne derivacije višeg
reda.
Primjer 1.24
Naći druge parcijalne derivacije funkcije
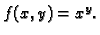
Rješenje.
Broj dervacija određenog reda raste eksponencijalno. Ipak, primjetite
da je u primjeru 1.24
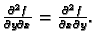 Uz neke uvjete to
vrijedi uvijek, kako pokazuje sljedeći teorem 5.
Uz neke uvjete to
vrijedi uvijek, kako pokazuje sljedeći teorem 5.
Teorem 5
(Schwartzov).
Neka funkcija

ima neprekidne druge
parcijalne derivacije na
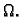
Tada je za svaki
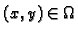
Dokaz.

Slično, uz pretpostavku da su treće parcijalne derivacije od  neprekidne,
imamo
neprekidne,
imamo
i također
U mnogim slučajevima su uvjeti Schwartzovog teorema ispunjeni, kao u primjeru 1.24. Dajmo primjer kada Schwartzov teorem ne vrijedi.
Primjer 1.25
Za funkciju
ne vrijedi Schwartzov teorem u
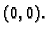
Rješenje. Doista
pa je
Tako je
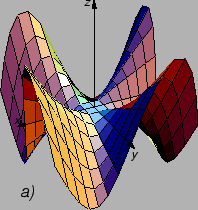
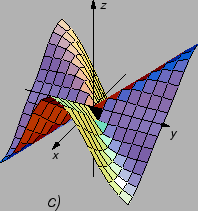
Slika
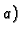
predstavlja graf funkcije
Slika
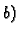
je graf
parcijalne derivacije

po
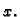
Iz slike se vidi da je njezina
derivacija po
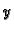
u ishodištu negativna (tangenta ponire kad idemo po
osi
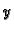
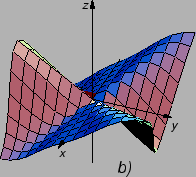
od manjih vrijednosti prema većim). Slika
je graf
parcijalne derivacije

po
Iz slike se vidi da je njezina
derivacija u ishodištu po

pozitivna (tangenta se penje kad idemo
u smjeru porasta vrijednosti po osi

).
Definicija 11
Za funkciju
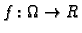
kažemo da je
klase
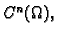
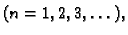
ako su njezine parcijalne derivacije
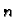
-tog
reda neprekidne funkcije na
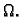
Kažemo da je funkcija
 klase
klase
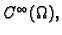
ako ima parcijalne derivacije bilo kojeg reda i ako su one
neprekidne na
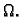
Razne su mogućnosti komponiranja funkcija više varijabli. Iskazat ćemo
teorem za jedan od jednostavnijih slučajeva, a zatim ćemo u primjerima
pokazati kako se postupa u drugim slučajevima.
Teorem 6
[
3]
Neka je

područje u
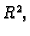
i neka je
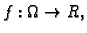
klase
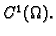
Neka je
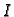
interval u
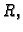
neka su
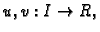
funkcije klase
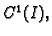
i neka je
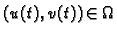
za
svaki
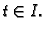
Tada postoji kompozicija
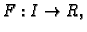
ona je klase
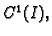
i vrijedi
Dokaz. Zaista,
Primjer 1.26
Derivirati funkciju
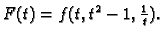
Rješenje.
Ako je dana funkcija
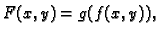 gdje je
gdje je 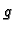 neprekidno
derivabilna funkcija od jedne varijable, onda imamo
neprekidno
derivabilna funkcija od jedne varijable, onda imamo
Primjer 1.27
Neka je
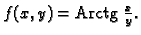
Treba naći
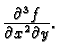
Rješenje. U ovom primjeru je
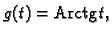 a
a
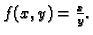 Tako imamo
Tako imamo
Sada dalje deriviramo dvaput po

po formuli za kvocijent
Primjer 1.28
Pokazati da funkcija
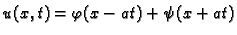
rješava
jednadžbu
Rješenje. Funkcije 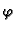 i
i 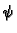 su funkcije od jedne varijable, a ta
varijabla je funkcija od dvije varijable
su funkcije od jedne varijable, a ta
varijabla je funkcija od dvije varijable  i
i 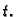 Tako imamo
Tako imamo
Ako komponiramo funkcije od više varijabli s funkcijama od više varijabli
na pr. 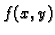 i
i
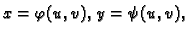 onda imamo
onda imamo
Slično
Derivacije višeg reda od složenih funkcija se računaju analogno. Na pr.
ako je
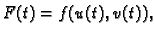 i ako su ispunjeni uvjeti Schwartzovog
teorema, onda
i ako su ispunjeni uvjeti Schwartzovog
teorema, onda
Ili, ako je
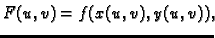 onda
onda
Pravilo po kojem smo računali u biti sve ove primjere se zove lančano pravilo.
Naziv dolazi odatle što se, u slučaju više varijabli, derivacije
konkateniraju operacijom zbrajanja.
- 1.
- Definirajte parcijalne derivacije funkcije više varijabli u
točki, i dajte geometrijsku interpretaciju.
- 2.
- Što je parcijalna derivacija funkcije?
- 3.
- Što su parcijalne derivacije višeg reda?
- 4.
- Što tvrdi Schwartzov teorem?
- 5.
- Što znači kad se kaže da je funkcija klase
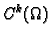 ?
?
- 6.
- Iskažite i dokažite teorem o derivaciji kompozicije funkcija.
- 7.
- Navedite primjere derivacija različitih kompozicija funkcija
više varijabli.
- 8.
- Zašto se pravilo za deriviranje kompozicije funkcija zove
lančano pravilo?
- 1.
- Jednadžba Clapeyrona glasi
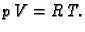 Ona daje vezu između
tlaka
Ona daje vezu između
tlaka 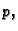 volumena
volumena 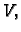 i temperature
i temperature 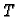 jednog mola plina.
jednog mola plina. 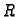 je
plinska konstanta. Izračunati
je
plinska konstanta. Izračunati
Rješenje. Imamo
pa je
- 2.
- Provjeriti ispravnost Schwartzovog teorema za funkciju
Rješenje.
- 3.
-
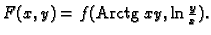 Naći
Naći
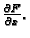
Rješenje.
- 4.
- Neka je dana funkcija
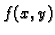 i
i
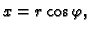
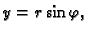 tako da je dana kompozicija
tako da je dana kompozicija
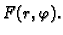 Naći
parcijalne derivacije.
Naći
parcijalne derivacije.
Rješenje.
- 5.
-
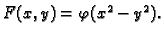 Naći
Naći
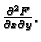
Rješenje.
- 6.
-
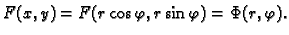 Izračunati
Izračunati
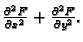
Rješenje.
Iz
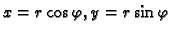 slijedi
Odatle
Nakon uvrštavanja i sređivanja dobivamo
slijedi
Odatle
Nakon uvrštavanja i sređivanja dobivamo
- 7.
- Ispitajte neprekidnost sljedeće funkcije i njezinih prvih i
drugih parcijalnih derivacija u ishodištu
Rješenje. Stavimo li
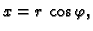
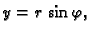 imamo
imamo
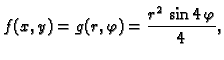
za
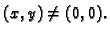
Ova funkcija ima u ishodištu limes 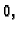 a kako je to i vrijednost
funkcije u ishodištu, funkcija
a kako je to i vrijednost
funkcije u ishodištu, funkcija  je neprekidna.
je neprekidna.
Izvan ishodišta je
funkcija racionalna, pa možemo koristiti pravila za deriviranje. Ako
osim toga pređemo na polarni koordinatni sustav, imamo
Niti jedna od ovih derivacija nije neprekidna u ishodištu, jer
očigledno ne postoje njihovi limesi u ishodištu.





Next: Teorem srednje vrijednosti
Up: Diferencijalni račun
Previous: Neprekidnost i limes
Contents
Index
Salih Suljagic
2000-03-11
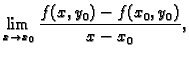
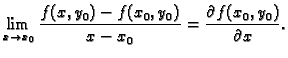
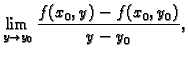
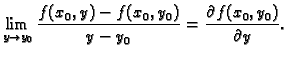
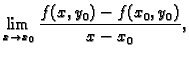
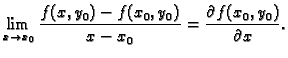
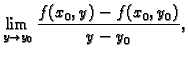
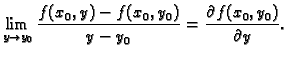
![]() funkcije
funkcije
![]() je krivulja,
koja se dobije kad se ploha
je krivulja,
koja se dobije kad se ploha ![]() presiječe ravninom
presiječe ravninom ![]() pa
je tako
pa
je tako
![]() koeficijent smjera
tangente na tu krivulju u točki
koeficijent smjera
tangente na tu krivulju u točki
![]()
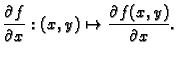
![]() po
po ![]()
![]() ove derivacije imaju vrijednosti
ove derivacije imaju vrijednosti
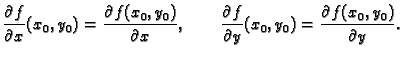
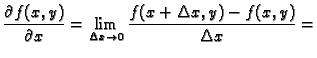
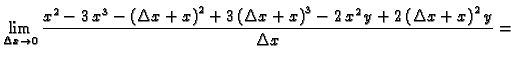
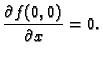
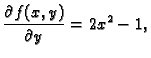
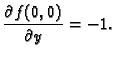
![]() onda imamo još jednu
parcijalnu derivaciju
onda imamo još jednu
parcijalnu derivaciju
![]() i t.d.
i t.d.
![]() funkcije
funkcije ![]() po
po
![]() ukoliko postoji, je također funkcija od dvije varijable
ukoliko postoji, je također funkcija od dvije varijable ![]() i
i
![]() Njezina parcijalna derivacija po
Njezina parcijalna derivacija po ![]() u točki
u točki
![]() ako
postoji, je
ako
postoji, je
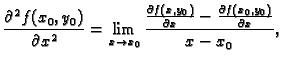
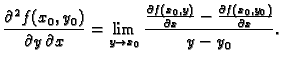
![]() dobivamo parcijalne
derivacije
dobivamo parcijalne
derivacije
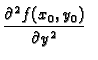 i
i 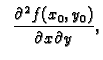
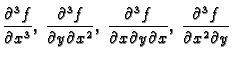
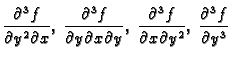
![]() Uz neke uvjete to
vrijedi uvijek, kako pokazuje sljedeći teorem 5.
Uz neke uvjete to
vrijedi uvijek, kako pokazuje sljedeći teorem 5.
![]()
![]() neprekidne,
imamo
neprekidne,
imamo
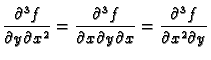
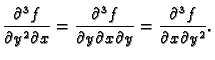
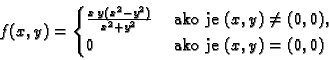
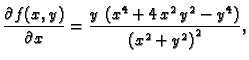
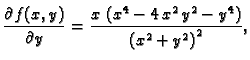
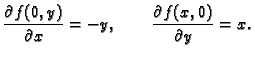
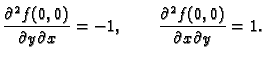
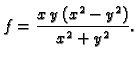
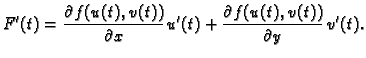
![$\displaystyle F'(t)=\lim_{\Delta t\rightarrow 0} \frac{F(t+\Delta t)-F(t)}{\Del...
...rightarrow 0} \frac{1}{\Delta t}
[f(u(t+\Delta t),v(t+\Delta t))-f(u(t),v(t))]=$](img455.gif)
![$\displaystyle \lim_{\Delta t\rightarrow 0} \frac{1}{\Delta t}
[f(u(t+\Delta t),v(t+\Delta t))-f(u(t),v(t+\Delta t))+
f(u(t),v(t+\Delta t))-f(u(t),v(t))]=$](img456.gif)
![$\displaystyle \lim_{\Delta t\rightarrow 0}
\left[\frac{\partial f(u(\tau),v(t+...
...al f(u(t),v(\sigma))}{\partial y}\,
\frac{v(t+\Delta t)-v(t)}{\Delta t}\right]=$](img457.gif)
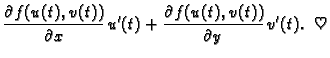
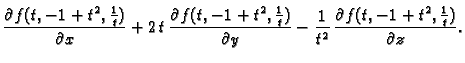
![]() gdje je
gdje je ![]() neprekidno
derivabilna funkcija od jedne varijable, onda imamo
neprekidno
derivabilna funkcija od jedne varijable, onda imamo
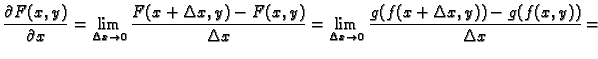
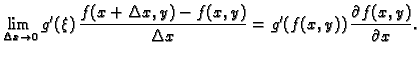
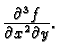
![]() a
a
![]() Tako imamo
Tako imamo
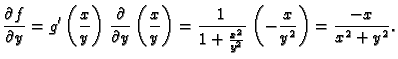
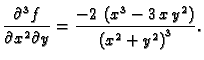
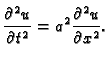
![]() i
i ![]() su funkcije od jedne varijable, a ta
varijabla je funkcija od dvije varijable
su funkcije od jedne varijable, a ta
varijabla je funkcija od dvije varijable ![]() i
i ![]() Tako imamo
Tako imamo
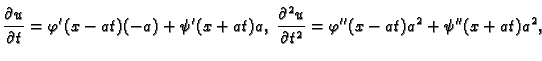
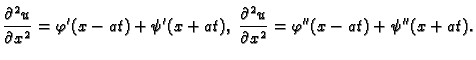
![]() i
i
![]() onda imamo
onda imamo
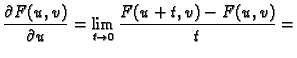
![$\displaystyle \lim_{t\rightarrow 0}
\frac{1}{t}
[f(\varphi(u+t,v),\psi(u+t,v))-f(\varphi(u,v),\psi(u,v))]=$](img479.gif)
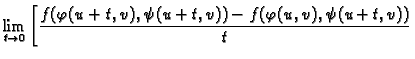
![$\displaystyle \left.+\frac{f(\varphi(u,v),\psi(u+t,v))-f(\varphi(u,v),\psi(u,v))}{t}\right]=$](img481.gif)
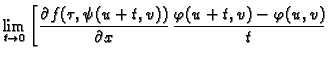
![$\displaystyle \left.+\frac{\partial f(\varphi(u,v),\sigma)}{\partial y}\,
\frac{\psi(u+t,v)-\psi(u,v)}{t}\right]=$](img483.gif)
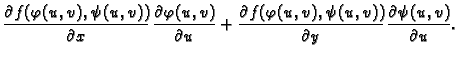
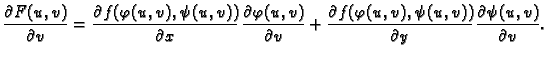
![]() i ako su ispunjeni uvjeti Schwartzovog
teorema, onda
i ako su ispunjeni uvjeti Schwartzovog
teorema, onda
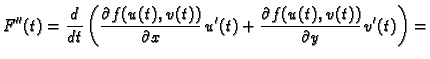
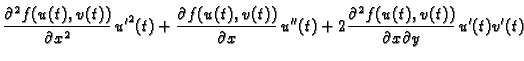
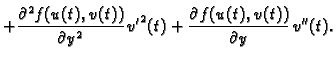
![$\displaystyle \frac{\partial^2 F}{\partial u\partial v}=
\frac{\partial}{\parti...
...\partial v}+
\frac{\partial f}{\partial y}\frac{\partial y}{\partial v}\right]=$](img491.gif)
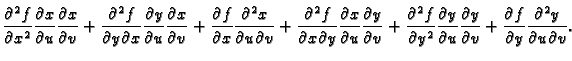
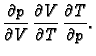
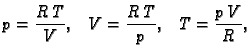
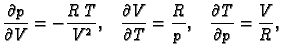
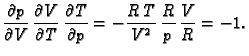
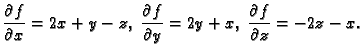
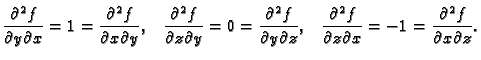
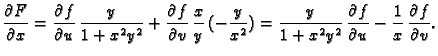
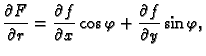
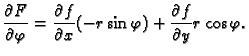
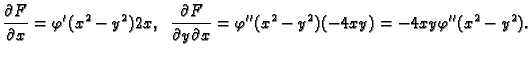
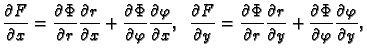
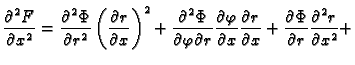
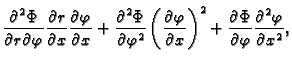
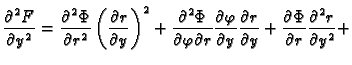
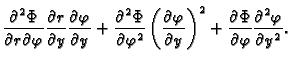
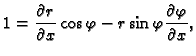
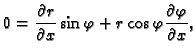
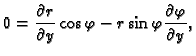
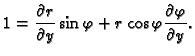
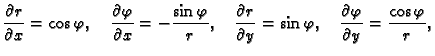
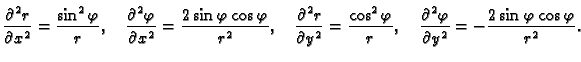
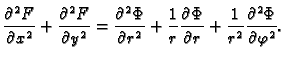
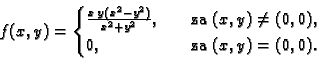
![]()
![]() imamo
imamo
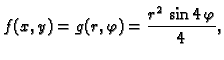 za
za