



Next: Pitanja
Up: Numerička matematika
Previous: Obične diferencijalne jednadžbe
Contents
Index
Subsections
Rješavanje parcijalnih diferencijalnih jednadžbi
Metoda konačnih diferencija
Rubne i rubno-početne probleme, u kojima se pojavljuju parcijalne
diferencijalne jednadžbe, možemo također rješavati metodom
konačnih diferencija, ili kako se u ovom slučaju često kaže
metodom mreže. Osnovna ideja je zamijeniti derivacije (u
ovom slučaju parcijalne) s konačnim diferencijama, i time svesti
parcijalnu diferencijalnu jednadžbu na sustav algebarskih jednadžbi.
Pokažimo kako se to u pojedinim slučajevima radi.
Jednadžba ravnoteže
Neka je dan rubni problem
gdje je 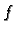 neprekidna funkcija na
neprekidna funkcija na
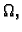 a
a 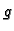 neprekidna na rubu
neprekidna na rubu
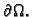
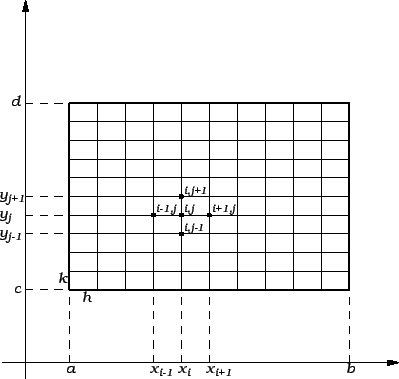
Područje 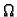 prekrijemo mrežom koju dobijemo tako da segmente
na osi
prekrijemo mrežom koju dobijemo tako da segmente
na osi 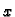 i osi
i osi 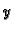 podijelimo ekvidistantno na podsegmenate. Tako
imamo
podijelimo ekvidistantno na podsegmenate. Tako
imamo
Broj 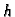 se zove korak mreže po
se zove korak mreže po 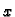 osi, a
osi, a 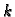 korak
mreže po
korak
mreže po 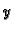 osi. Tako imamo točke podjele
na osima. Točku s koordinatama
zovemo
osi. Tako imamo točke podjele
na osima. Točku s koordinatama
zovemo 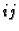 -tim čvorom mreže. Čvor zovemo
unutrašnjim, ako je
-tim čvorom mreže. Čvor zovemo
unutrašnjim, ako je
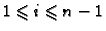 i
i
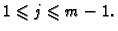 U protivnom kažemo da je čvor
rubni. Stavimo
Kao i u slučaju običnih derivacija, aproksimacije parcijalnih
derivacija možemo dobiti pomoću Taylorove formule za funkcije od
dvije varijable. Tako imamo
Neka je
U protivnom kažemo da je čvor
rubni. Stavimo
Kao i u slučaju običnih derivacija, aproksimacije parcijalnih
derivacija možemo dobiti pomoću Taylorove formule za funkcije od
dvije varijable. Tako imamo
Neka je 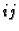 unutrašnji čvor. Tada diferencijalnu jednadžbu u tom
čvoru možemo zamijeniti algebarskom jednadžbom
Ako je čvor
unutrašnji čvor. Tada diferencijalnu jednadžbu u tom
čvoru možemo zamijeniti algebarskom jednadžbom
Ako je čvor 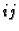 rubni, onda imamo
Time smo dobili onoliko linearnih algebarskih
jednadžbi koliko imamo nepoznanica
rubni, onda imamo
Time smo dobili onoliko linearnih algebarskih
jednadžbi koliko imamo nepoznanica 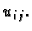 Rješavati treba samo
sustav jednadžbi unutrašnjih čvorova. Pretpostavimo, radi
jednostavnosti, da su
Rješavati treba samo
sustav jednadžbi unutrašnjih čvorova. Pretpostavimo, radi
jednostavnosti, da su
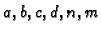 takvi da je
takvi da je 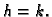 Tada, nakon
množenja s
Tada, nakon
množenja s 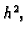 jednadžba
jednadžba 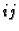 -tog čvora postaje
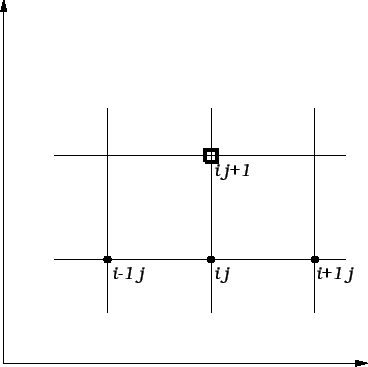
Vidimo da u svakom retku matrice ima najviše pet elemenata
različitih od nule. Na sljedećoj slici su istaknuti oni čvorovi, koji imaju svojstvo da vrijednosti funkcije
-tog čvora postaje
Vidimo da u svakom retku matrice ima najviše pet elemenata
različitih od nule. Na sljedećoj slici su istaknuti oni čvorovi, koji imaju svojstvo da vrijednosti funkcije  u njima nalaze u jednadžbi.
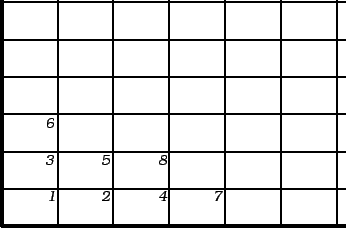
Jednadžbe trebamo na neki način poredati. To možemo učiniti tako
da čvorove poredamo. Njih možemo poredati na različite načine.
Jedan od njih je poredak kao na slici
Dakle
Stavimo
Na taj način dobivamo sljedeći sustav linearnih algebarskih
jednadžbi
u njima nalaze u jednadžbi.
Jednadžbe trebamo na neki način poredati. To možemo učiniti tako
da čvorove poredamo. Njih možemo poredati na različite načine.
Jedan od njih je poredak kao na slici
Dakle
Stavimo
Na taj način dobivamo sljedeći sustav linearnih algebarskih
jednadžbi
Prilikom izbora poretka treba paziti na to da matrica dobivenog
sustava jednadžbi bude što uža.
Jednadžba provođenja
Jednodimenzionalno provođenje topline opisano je sljedećim
rubno-početnim problemom
Neka je
korak mreže po osi  a
a 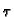 korak po osi
korak po osi 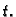 Tako imamo točke podjele na
Tako imamo točke podjele na 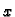 osi, odnosno
osi, odnosno 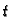 osi
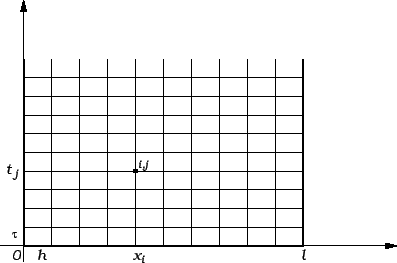
Interesira nas što se događa u čvorovima, tj. točkama
Stavimo
Iz rubnih i početnih uvjeta slijedi
Dakle ostaje odrediti
osi
Interesira nas što se događa u čvorovima, tj. točkama
Stavimo
Iz rubnih i početnih uvjeta slijedi
Dakle ostaje odrediti 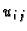 u unutrašnjim čvorovima. U tu svrhu
derivacije aproksimiramo koristeći neke od mogućih formula, na pr.
U unutrašnjem čvoru
u unutrašnjim čvorovima. U tu svrhu
derivacije aproksimiramo koristeći neke od mogućih formula, na pr.
U unutrašnjem čvoru 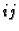 diferencijalna jednadžba postaje
Pomnožimo jednadžbu s
diferencijalna jednadžba postaje
Pomnožimo jednadžbu s 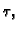 i stavimo
Tada jednadžba u čvoru
i stavimo
Tada jednadžba u čvoru 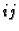 glasi
glasi
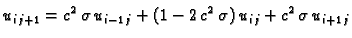 |
(3.33) |
Sada, za razliku od postupka kod jednadžbe ravnoteže, rješenje tražimo
sukcesivno. Zahvaljujući upotrebljenoj diferencijskoj shemi,
najprije računamo 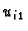 po formuli (3.33)
Zatim formulom (3.33) za
po formuli (3.33)
Zatim formulom (3.33) za 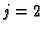 računamo
računamo 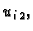 itd.
itd.
Da bi ovako definiran postupak bio korektan, on treba biti
-
- konvergentan, tj. sa smanjivanjem koraka mora
približno rješenje težiti k točnom rješenju, i
-
- stabilan, tj. male promjene ulaznih podataka
(greške zaokruživanja) ne smiju prouzročiti velike razlike u rješenju.
Može se pokazati da su oba uvjeta ispunjena, ako je
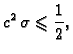
tj.
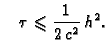
Ovdje opisan postupak rješavanja, zasnovan na formuli
(3.33) se zove eksplicitan. On je kao što se
vidi vrlo jednostavan. Nedostatak postupka je u tome što se zbog
potrebe stabilnosti i konvergencije mora korak po osi 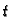 uzeti vrlo
malen. Za
uzeti vrlo
malen. Za 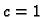 i
i 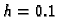 treba biti
treba biti
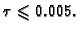 Postoji
implicitni postupak, kod kojeg nema zahtjeva na
Postoji
implicitni postupak, kod kojeg nema zahtjeva na 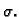 Međutim on
vodi na rješavanje sustava jednadžbi, pa se tu pojavljuju drugi
problemi, osobito kad su koraci maleni. Osim toga kod implicitnog
postupka moramo unaprijed ograničiti vrijeme, kako bismo imali
konačno mnogo čvorova, dok kod eksplicitnog postupka ne treba
unaprijed ograničavati vrijeme.
Međutim on
vodi na rješavanje sustava jednadžbi, pa se tu pojavljuju drugi
problemi, osobito kad su koraci maleni. Osim toga kod implicitnog
postupka moramo unaprijed ograničiti vrijeme, kako bismo imali
konačno mnogo čvorova, dok kod eksplicitnog postupka ne treba
unaprijed ograničavati vrijeme.
Valna jednadžba
Problem koji sada rješavamo je
Diskretizaciju područja učinimo kao kod jednadžbe
provođenja. Razlika je u tome što u jednadžbi dolazi druga
parcijalna derivacija po 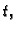 i što imamo dodatni početni
uvjet. Parcijalnu derivaciju iz početnog uvjeta možemo na razne
načine aproksimirati diferencijama. Neka je na pr.
U unutrašnjem čvoru
i što imamo dodatni početni
uvjet. Parcijalnu derivaciju iz početnog uvjeta možemo na razne
načine aproksimirati diferencijama. Neka je na pr.
U unutrašnjem čvoru 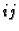 jednadžba je
Nakon množenja s
jednadžba je
Nakon množenja s 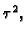 i stavljanja
imamo eksplicitni postupak dan formulom
i stavljanja
imamo eksplicitni postupak dan formulom
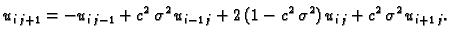 |
(3.34) |
Vrijednosti u prva dva reda čvorova 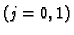 dobijemo iz početnih
uvjeta. Vrijednosti u daljnjim redovima računamo sukcesivno pomoću
formule (3.34). Za
dobijemo iz početnih
uvjeta. Vrijednosti u daljnjim redovima računamo sukcesivno pomoću
formule (3.34). Za
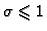 postupak je
stabilan.
postupak je
stabilan.
Varijacijske metode
Ritzova metoda
Pogledajmo kako ona funkcionira kad se radi o rubnom
problemu
Kao u jednodimenzionalnom slučaju izaberemo 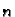 linearno nezavisnih
funkcija
linearno nezavisnih
funkcija
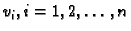 koje zadovoljavaju rubni
uvjet. Rješenje se pretpostavi u obliku
i neodređeni koeficijenti se odrede
iz uvjeta da
koje zadovoljavaju rubni
uvjet. Rješenje se pretpostavi u obliku
i neodređeni koeficijenti se odrede
iz uvjeta da 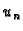 minimizira pripadni funkcional energije
Tako dobiveni
minimizira pripadni funkcional energije
Tako dobiveni 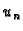 leži u vektorskom prostoru razapetom s
funkcijama
leži u vektorskom prostoru razapetom s
funkcijama 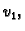
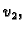
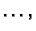
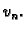 Rješenje ne mora ležati u tom
prostoru, pa u tom slučaju
Rješenje ne mora ležati u tom
prostoru, pa u tom slučaju 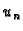 nije točno već samo približno
rješenje. No, što veći
nije točno već samo približno
rješenje. No, što veći 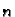 uzmemo, to je manja greška koju činimo
prihvaćajući
uzmemo, to je manja greška koju činimo
prihvaćajući 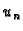 kao rješenje problema.
kao rješenje problema.
Prvi problem s kojim se susrećemo kod Ritzove metode je određivanje
funkcija 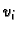 koje moraju zadovoljavati rubni uvjet. Ako područje
nije dovoljno lijepo, mogu nastati problemi. Nakon što smo izabrali
funkcije
koje moraju zadovoljavati rubni uvjet. Ako područje
nije dovoljno lijepo, mogu nastati problemi. Nakon što smo izabrali
funkcije 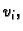 pretpostavljeno rješenje uvrstimo u funkcional
pretpostavljeno rješenje uvrstimo u funkcional
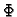 je derivabilna funkcija od
je derivabilna funkcija od 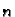 varijabli
varijabli
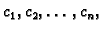 pa jednadžbe
za
pa jednadžbe
za
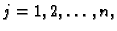 predstavljaju nužan uvjet za ekstrem funkcije
predstavljaju nužan uvjet za ekstrem funkcije
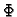 u točki
u točki
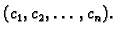 Ovo je sustav od
Ovo je sustav od 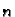 linearnih algebarskih
jednadžbi od
linearnih algebarskih
jednadžbi od 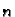 nepoznanica. Stavimo
Sada se sustav može kratko zapisati
gdje je
nepoznanica. Stavimo
Sada se sustav može kratko zapisati
gdje je
![$ \boldsymbol{K}=[K_{ij}],\boldsymbol{c}=[c_j],\boldsymbol{b}=[b_i].$](img3529.gif)
Nedostaci ove metode su u tome što je za proizvoljno područje teško
naći funkcije 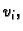 i u tome što je matrica
i u tome što je matrica
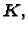 koja
se inače zove matrica krutosti, puna matrica, tj. općenito
je svaki njezin element različit od nule.
koja
se inače zove matrica krutosti, puna matrica, tj. općenito
je svaki njezin element različit od nule.
Metoda konačnih elemenata
Navedene nedostatke donekle ispravlja metoda konačnih elemenata.
Područje 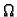 podijelimo jednostavnim likovima (trokutima
četverokutima i sl.) na dijelove, elemente. Vrhove elemenata
zovemo čvorovima. Podjela se vrši tako da niti jedan čvor
ne leži na stranici nekog drugog čvora. Numeriramo elemente i
čvorove. Čvorove treba pažljivo numerirati, da matrica sustava
koji ćemo konačno dobiti bude što uža, tj. da pojas oko glavne
dijagonale izvan kojeg su same nule bude što uži. Zatim odaberemo
koordinatne funkcije
podijelimo jednostavnim likovima (trokutima
četverokutima i sl.) na dijelove, elemente. Vrhove elemenata
zovemo čvorovima. Podjela se vrši tako da niti jedan čvor
ne leži na stranici nekog drugog čvora. Numeriramo elemente i
čvorove. Čvorove treba pažljivo numerirati, da matrica sustava
koji ćemo konačno dobiti bude što uža, tj. da pojas oko glavne
dijagonale izvan kojeg su same nule bude što uži. Zatim odaberemo
koordinatne funkcije
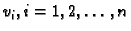 tako da
tako da 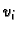 u čvoru
u čvoru 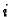 ima vrijednost
ima vrijednost 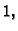 a u ostalim čvorovima vrijednost
a u ostalim čvorovima vrijednost 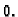 Na
elementima, koji nemaju čvor
Na
elementima, koji nemaju čvor 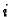 kao vrh,
kao vrh, 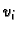 ima vrijednost
ima vrijednost 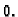 Na elementima, koji imaju čvor
Na elementima, koji imaju čvor 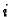 kao svoj vrh, funkciju
kao svoj vrh, funkciju 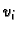 definiramo kao polinom prvog stupnja ili viših stupnjeva ako to
zahtijeva problem koji rješavamo. Objasnimo sada na jednom
jednostavnom primjeru metodu konačnih elemenata za problem ravnoteže
membrane.
definiramo kao polinom prvog stupnja ili viših stupnjeva ako to
zahtijeva problem koji rješavamo. Objasnimo sada na jednom
jednostavnom primjeru metodu konačnih elemenata za problem ravnoteže
membrane.
Primjer 3.22
Neka na napetu kvadratnu membranu duljine stranice
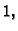
učvršćene
na rubu u ravnini
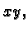
djeluje vanjska sila u smjeru osi
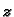
po
iznosu jednaka
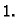
Treba naći ravnotežni položaj membrane.
Rješenje. Rubni problem za ovaj zadatak glasi, uz dodatnu pretpostavku da je
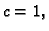
gdje je
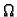
kvadrat stranice
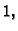
koji možemo uzeti u ravnini
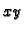
tako da su mu vrhovi točke
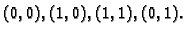
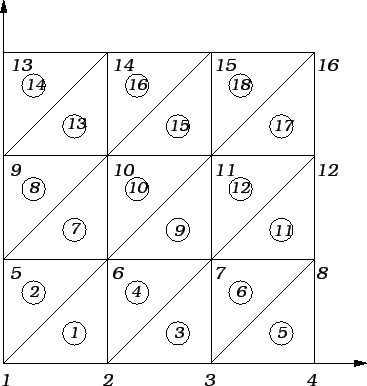
Podijelimo
na devet jednakih kvadrata i zatim svaki od tih kvadrata na dva
trokuta. Time je
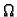
podijeljen na 18 elemenata
(trokuta). Također imamo 16 čvorova, od toga 12 na rubu. To su
točke
Na ovoj slici su brojevima označeni čvorovi, a brojevima u
kružnicama konačni elementi (u ovom slučaju trokuti).
Funkcional energije u ovom slučaju je
Za svaki čvor definiramo koordinatnu funkciju
tako da stavimo
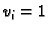
u
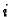
-tom čvoru, a u ostalim čvorovima
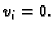
Na elementu
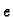
koji ima
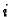
-ti čvor kao vrh stavimo
Za
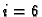
imamo
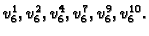
Nađimo na
pr.
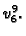
Zbog svojstva koordinatnih funkcija imamo
Rješenje je
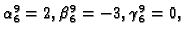
pa je
Na isti način možemo naći da je
a također i ostale koordinatne funkcije. Primijetimo da je zbog
geometrijskih razloga
Rješenje tražimo u obliku
U čvoru na rubu, na pr. prvom,
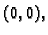
funkcija

se
poništava. Dakle
U prvom čvoru funkcija
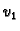
prima vrijednost
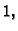
a ostale funkcije
primaju vrijednost
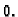
Tako imamo
Za svaki čvor na rubu možemo na taj način dobiti da je, zbog uvjeta
na rubu, pripadni koeficijent jednak
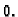
Tako imamo
Preostaje dakle
Dakle zadatak je odrediti koeficijente
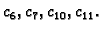
To
ćemo učiniti tako da u Bernoullijev princip (
2.12)
uvrstimo ovaj
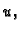
i redom
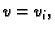
gdje je
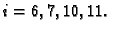
Tako imamo
Da bi se dobila jednadžba za čvor
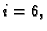
treba izračunati
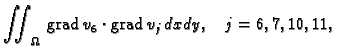
i
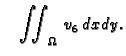
Integral po
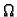
je suma integrala po elementima. Zbog svojstava
koordinatnih funkcija, integral po mnogim elementima iščezava. Na
pr.
Tako je
i prema tome
Zatim
pa je
i prema tome
pa je
i prema tome
pa je
i prema tome
Osim toga je
Isti rezultat dobivamo i ako umjesto
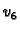
stavimo
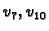
ili
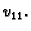
Tako je jednadžba za čvor
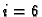
Također je očito
pa jednadžba za čvor
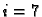
glasi
pa jednadžbe za čvorove
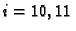
glase
Rješenje sustava je
To su ujedno vrijednosti funkcije

u čvorovima
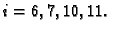
Za zapisivanje brojeva općenito, pa i u kompjuteru, koristi se niz
znamenaka u nekom brojevnom sustavu. U tu svrhu treba odrediti
bazu 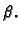 Na pr. u dekadskom sustavu je
Na pr. u dekadskom sustavu je 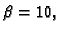 a u
binarnom
a u
binarnom 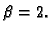 Računati ne možemo s beskonačno mnogo
znamenaka. To ne može niti kompjuter. Dapače, on je ograničen
svojim fizičkim mogućnostima, hardwareom. Ograničenje se odnosi na
broj znamenaka
Računati ne možemo s beskonačno mnogo
znamenaka. To ne može niti kompjuter. Dapače, on je ograničen
svojim fizičkim mogućnostima, hardwareom. Ograničenje se odnosi na
broj znamenaka 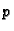 koje može upotrebiti za zapis jednog broja. Broj
koje može upotrebiti za zapis jednog broja. Broj
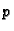 se zove preciznost. Uređeni par
se zove preciznost. Uređeni par 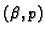 zove se
format.
zove se
format.
Cijeli brojevi se u kompjuteru zapisuju u formatu 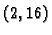 ili
ili
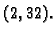 Dakle radi se o brojevima koji se zapisuju pomoću znamenki
0 i
Dakle radi se o brojevima koji se zapisuju pomoću znamenki
0 i 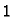 razmještenih na
razmještenih na 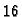 ili
ili 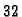 mjesta. Pri tom se prvo
mjesto koristi za predznak. Broj 0 označava pozitivan broj,
mjesta. Pri tom se prvo
mjesto koristi za predznak. Broj 0 označava pozitivan broj, 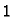 negativan. Pojedino mjesto na koje možemo upisati jednu znamenku zove
se bit.
negativan. Pojedino mjesto na koje možemo upisati jednu znamenku zove
se bit.
Imamo sljedeći algoritam za pretvaranje broja zapisanog u
dekadskom sustavu u binarni.
Algoritam 13
Neka je
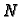
dekadski zapis broja. Računamo
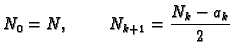
za
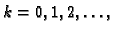
gdje je
Račun provodimo sve dok ne dobijemo
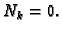
Primjer 3.23
Treba za broj koji ima dekadski zapis
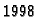
naći binarni zapis.
Rješenje.
Dakle binarni zapis je
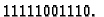
Tako se u formatu 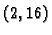 dekadski broj
dekadski broj 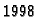 zapisuje kao
zapisuje kao
Segment određen donjom i gornjom granicom zapisa zove se
rang. Budući da u formatu 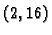 imamo
imamo 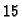 bitova za upis
znamenaka (jedan bit je rezerviran za predznak), i budući da se mogu
koristiti samo znamenke 0 i
bitova za upis
znamenaka (jedan bit je rezerviran za predznak), i budući da se mogu
koristiti samo znamenke 0 i 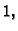 najveći broj koji tako možemo
zapisati je
Najmanji cijeli broj koji se tako može zapisati je
najveći broj koji tako možemo
zapisati je
Najmanji cijeli broj koji se tako može zapisati je 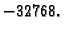 Tako je
rang u ovom slučaju
Tako je
rang u ovom slučaju
Ovakav zapis brojeva se zove zapis pomoću fiksnog zareza
(fixed-point). U aritmetici foksnog zareza postoje greške, no mi
ćemo se ovdje ograničiti samo na neke aspekte pojave grešaka kod
zapisa i raračunanja s realnim brojevima.
Za kompjuterski zapis realnog broja obično se koristi format 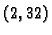 ili
ili
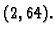 Za prvi format se kaže da se radi o jednostrukoj, a za
drugi o dvostrukoj preciznosti.
Za prvi format se kaže da se radi o jednostrukoj, a za
drugi o dvostrukoj preciznosti.
U formatu 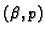 realni broj se zapisuje u obliku
realni broj se zapisuje u obliku
gdje su 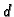 znamenke
znamenke
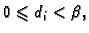 a
a 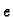 je eksponent. Tako je u
formatu
je eksponent. Tako je u
formatu 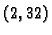
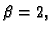
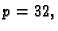 a znamenke
a znamenke 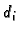 su 0 ili
su 0 ili 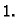 U
tom formatu prvi bit određuje predznak, a zadnjih osam eksponent, od
kojih prvi određuje predznak eksponenta.
Realan broj se uvijek zapisuje u
normaliziranom obliku, tj. u
obliku u kojem je
U
tom formatu prvi bit određuje predznak, a zadnjih osam eksponent, od
kojih prvi određuje predznak eksponenta.
Realan broj se uvijek zapisuje u
normaliziranom obliku, tj. u
obliku u kojem je
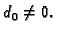 To je zato da bi zapis broja bio
jedinstven. Rang u ovom slučaju određuju minimalni i maksimalni
eksponent. Maksimalni je
dok je
To je zato da bi zapis broja bio
jedinstven. Rang u ovom slučaju određuju minimalni i maksimalni
eksponent. Maksimalni je
dok je
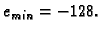 Rang određujemo tako da nađemo onaj
Rang određujemo tako da nađemo onaj 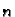 za
koji je
Ako logaritmiramo, imamo
Dakle rang je
Ovakav zapis broja zovemo zapisom pomoću pomičnog zareza
(floating-point).
za
koji je
Ako logaritmiramo, imamo
Dakle rang je
Ovakav zapis broja zovemo zapisom pomoću pomičnog zareza
(floating-point).
Greške nastaju na dva načina. Jedan način da nastane
greška je taj da se slijedom operacija dođe do broja koji nije u
rangu. U tom slučaju kažemo da se dogodio overflow. O tome nećemo govoriti. Drugi način kako
može doći do greške jeste kada želimo upisati ili kad
operacijama dođemo do broja koji se ne može točno zapisati u
formatu u kojem radi kompjuter. Na pr. dekadski broj 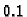 se ne može točno zapisati u formatu s bazom
se ne može točno zapisati u formatu s bazom 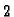 bez obzira kolika
bila preciznost.
bez obzira kolika
bila preciznost.
Pretvorba dekadskog zapisa u binarni u slučaju realnog broja
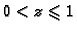 dan je ovim algoritmom.
dan je ovim algoritmom.
Algoritam 14
Neka je
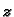
takav da je
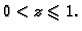
Računamo nizove brojeva
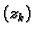
i
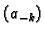
iz formula
Tada je
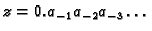
binarni zapis broja
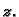
Pomoću ovog algoritma možemo utvrditi da binarni zapis dekadskog
broja 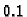 glasi
glasi
U zapisu pomoću pomičnog zareza je
pa je relativna greška
Ako je 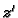 najbolja moguća aproksimacija broja
najbolja moguća aproksimacija broja 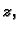 onda je
apsolutna greška (brojnik ovog razlomka) najviše
Brojevi oblika
onda je
apsolutna greška (brojnik ovog razlomka) najviše
Brojevi oblika
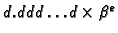 se nalaze između
se nalaze između
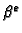 i
i
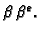 Prema tome najveća moguća
relativna greška je
Ovaj broj se zove kompjuterski epsilon. Najmanja moguća
relativna greška je
Tako je
Prema tome najveća moguća
relativna greška je
Ovaj broj se zove kompjuterski epsilon. Najmanja moguća
relativna greška je
Tako je
Osim relativnom greškom, grešku možemo mjeriti i jedinicom
ulp (units in the last place). Ako
je format
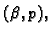 onda se greška u ulpima izražava formulom
onda se greška u ulpima izražava formulom
Primjer 3.24
Neka je format
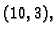
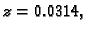
i
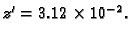
Naći grešku u ulpima.
Rješenje.
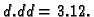 Zatim
Zatim 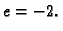 Odatle
Odatle
Greška u ulpima omogućava da odredimo broj nepouzdanih znamenki u
približnoj vrijednosti 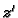 broja
broja 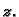 Ako je greška
Ako je greška 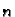 ulpa, onada
je broj nepouzdanih znamenki
ulpa, onada
je broj nepouzdanih znamenki
Primjer 3.25
U formatu
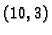
treba izračunati
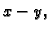
ako je
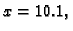
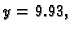
i odrediti broj nepouzdanih znamenki približne
vrijednosti.
Rješenje. Prilikom zbrajanja ili odbijanja manji broj svodimo na potenciju
baze većega, i zatim zbrajamo samo signifikande
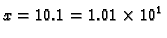
i
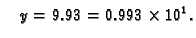
Odatle
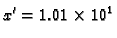
i
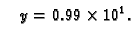
Tako je
dok je točna vrijednost
Greška u ulpima je prema tome
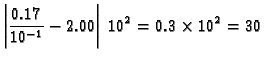
ulpa.
Budući da je
nepouzdane su dvije znamenke.
U ovom primjeru je 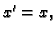 a greška zaokruživanja broja
a greška zaokruživanja broja 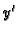 je
je
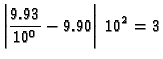
ulpa.
Dakle u
je jedna znamenka nepouzdana. Ipak prilikom odbijanja se broj
nepouzdanih znamenki povećao. Dapače, kad se odbijaju bliski brojevi
može se dogoditi da niti jedna znamenka u rezultatu nije pouzdana.
Taj problem se može ublažiti tako da se račun izvede s dodatnom
znamenkom (guard digit).
Primjer 3.26
Riješimo primjer
3.25 pomoću dodatne znamenke.
Rješenje. Tada je
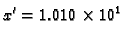
i
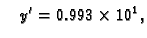
pa je
što je točna vrijednost.
Primjer 3.27
Neka je format
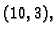
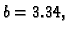
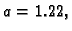
i
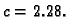
Treba
izračunati
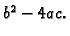
Rješenje.
Dakle greška je
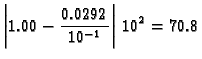
ulpa.
Prema tome dvije znamenke su nepouzdane.
Ako se radi s dodatnom znamenkom, greška postaje samo 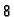 ulpa.
ulpa.
Osim računanjem s dodatnom znamenkom, greška se može umanjiti
rearanžiranjem formule.
Primjer 3.28
Ako je
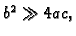
i
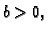
onda je
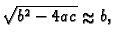
pa formula
sadrži odbijanje bliskih
brojeva, što može dovesti do velike pogreške. U ovom slučaju
možemo racionalizirati brojnik
Primjer 3.29
Heronova formula za računanje površine trokuta glasi
gdje je
Neka je dan trokut takav da je
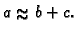
Tada ova formula daje loš rezultat za površinu. Znatno bolja
je formula
Primjer 3.30
Format je
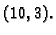
Treba izračunati
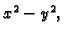
ako je
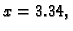
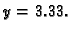
Rješenje. Točan rezultat je
Računanje po formuli
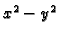
daje
Ovaj račun daje grešku od
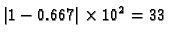
ulpa
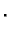
No, ako računamo po formuli
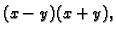
onda imamo
Tako je
što je točan rezultat.
Primjer 3.31
Format je
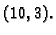
Treba izračunati
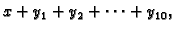
gdje je
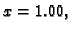
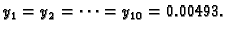
Rješenje. Točan rezultat je
Ako računamo po formuli
onda imamo
jer se prilikom
zbrajanja ili odbijanja brojevi poravnavaju po eksponentu najvećega,
i zatim zaokružuju. Tako imamo
Nakon toga, na isti način
itd. Na kraju imamo
Ako računamo tako da najprije zbrojimo male brojeve, pa zatim dodamo
 onda imamo
onda imamo
pa je
Odatle
Da se ovaj broj pribroji broju
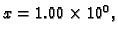
mora ga se svesti na potenciju s eksponentom
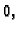
zaokružiti ga i zatim dodati
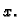
To znači
pa je i
Ako se koristi dodatna znamenka (guard digit) prilikom zaokruživanja,
pa se zatim rezultat na kraju zaokruži, greška naravno može biti
veća nego ako se točan rezultat na kraju zaokruži.
Ako se operacije izvode točno, pa se konačni rezultat zaokruži na
najbliži kompjuterski realni broj, onda kažemo da je
zaokruživanje točno. Međutim, kompjuteru treba reći koji
je to najbliži broj. Da problem bude jasniji, ostanimo kod baze 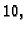 i preciznosti
i preciznosti 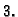 Za broj
Za broj 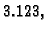 ili
ili 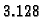 jasno je kako ćemo ga
zaokružiti. Ako je znamenka koja se odbacuje manja od
jasno je kako ćemo ga
zaokružiti. Ako je znamenka koja se odbacuje manja od 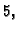 onda se
prethodna znamenka ne mijenja. Ako je znamenka koja se odbacuje veća
od
onda se
prethodna znamenka ne mijenja. Ako je znamenka koja se odbacuje veća
od 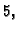 onda se prethodna znamenka uveća za jedan. Postavlja se
pitanje kako zaokružiti broj
onda se prethodna znamenka uveća za jedan. Postavlja se
pitanje kako zaokružiti broj 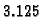 ? Jedan način je da se prethodna znamenka uveća za jedan. To može dovesti do velike greške.
? Jedan način je da se prethodna znamenka uveća za jedan. To može dovesti do velike greške.
Primjer 3.32
Prema rekurzivnoj formuli
treba mnogo puta računati rezultat.
Rješenje. Radi jednostavnosti uzmimo format 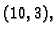
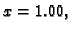
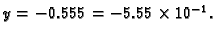 Imamo
Imamo 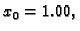
Dobivamo sve veće brojeve. Tako na primjer
Drugi način bi bio da se brojevi, kod kojih je broj 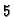 prva znamenka
koja se odbacuje, u pola slučajeva zaokružuju odbacivanjem, a u
drugih pola uvećavanjem prethodne znamenke za jedan. Pravilo može
biti na pr. sljedeće.
prva znamenka
koja se odbacuje, u pola slučajeva zaokružuju odbacivanjem, a u
drugih pola uvećavanjem prethodne znamenke za jedan. Pravilo može
biti na pr. sljedeće.
- -
- Ako je znamenka ispred broja
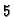 parna, onda se
parna, onda se 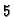 odbacuje.
odbacuje.
- -
- Ako je znamenka ispred broja
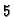 neparna, onda se
neparna, onda se 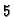 odbacuje, a prethodna znamenka se uvećava za jedan.
odbacuje, a prethodna znamenka se uvećava za jedan.
Lako se vidi da primjenjujući ovo pravilo u prethodnom primjeru
dobivamo točan rezultat.




Next: Pitanja
Up: Numerička matematika
Previous: Obične diferencijalne jednadžbe
Contents
Index
Salih Suljagic
1999-12-17
![]() prekrijemo mrežom koju dobijemo tako da segmente
na osi
prekrijemo mrežom koju dobijemo tako da segmente
na osi ![]() i osi
i osi ![]() podijelimo ekvidistantno na podsegmenate. Tako
imamo
podijelimo ekvidistantno na podsegmenate. Tako
imamo
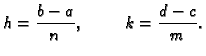
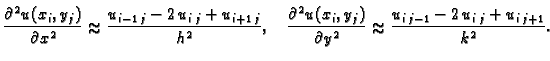
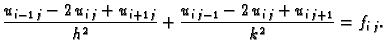
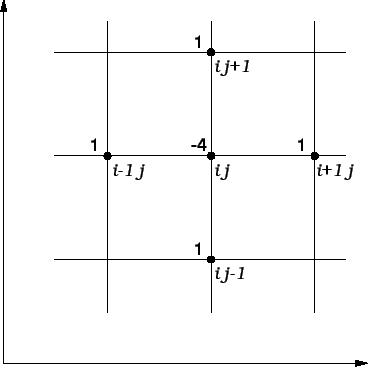
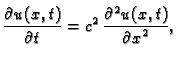
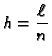
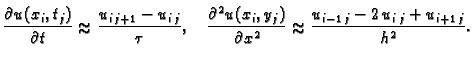
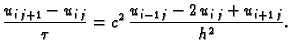
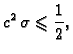 tj.
tj.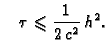
![]() uzeti vrlo
malen. Za
uzeti vrlo
malen. Za ![]() i
i ![]() treba biti
treba biti
![]() Postoji
implicitni postupak, kod kojeg nema zahtjeva na
Postoji
implicitni postupak, kod kojeg nema zahtjeva na ![]() Međutim on
vodi na rješavanje sustava jednadžbi, pa se tu pojavljuju drugi
problemi, osobito kad su koraci maleni. Osim toga kod implicitnog
postupka moramo unaprijed ograničiti vrijeme, kako bismo imali
konačno mnogo čvorova, dok kod eksplicitnog postupka ne treba
unaprijed ograničavati vrijeme.
Međutim on
vodi na rješavanje sustava jednadžbi, pa se tu pojavljuju drugi
problemi, osobito kad su koraci maleni. Osim toga kod implicitnog
postupka moramo unaprijed ograničiti vrijeme, kako bismo imali
konačno mnogo čvorova, dok kod eksplicitnog postupka ne treba
unaprijed ograničavati vrijeme.
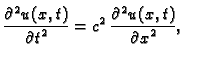
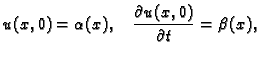
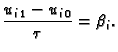
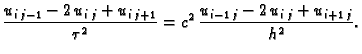
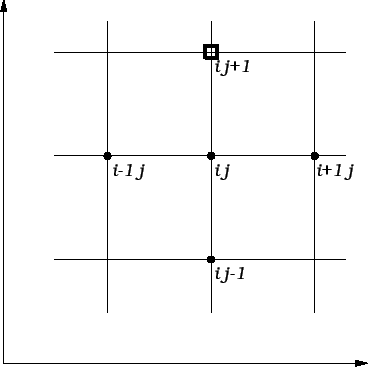
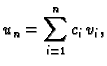
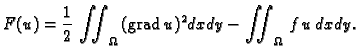
![]() koje moraju zadovoljavati rubni uvjet. Ako područje
nije dovoljno lijepo, mogu nastati problemi. Nakon što smo izabrali
funkcije
koje moraju zadovoljavati rubni uvjet. Ako područje
nije dovoljno lijepo, mogu nastati problemi. Nakon što smo izabrali
funkcije ![]() pretpostavljeno rješenje uvrstimo u funkcional
pretpostavljeno rješenje uvrstimo u funkcional
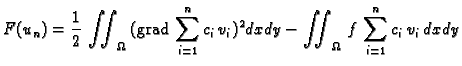
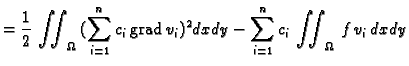
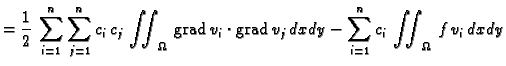
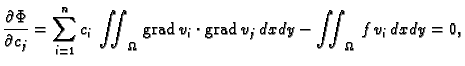
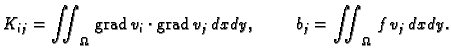
![]() i u tome što je matrica
i u tome što je matrica
![]() koja
se inače zove matrica krutosti, puna matrica, tj. općenito
je svaki njezin element različit od nule.
koja
se inače zove matrica krutosti, puna matrica, tj. općenito
je svaki njezin element različit od nule.
![]() podijelimo jednostavnim likovima (trokutima
četverokutima i sl.) na dijelove, elemente. Vrhove elemenata
zovemo čvorovima. Podjela se vrši tako da niti jedan čvor
ne leži na stranici nekog drugog čvora. Numeriramo elemente i
čvorove. Čvorove treba pažljivo numerirati, da matrica sustava
koji ćemo konačno dobiti bude što uža, tj. da pojas oko glavne
dijagonale izvan kojeg su same nule bude što uži. Zatim odaberemo
koordinatne funkcije
podijelimo jednostavnim likovima (trokutima
četverokutima i sl.) na dijelove, elemente. Vrhove elemenata
zovemo čvorovima. Podjela se vrši tako da niti jedan čvor
ne leži na stranici nekog drugog čvora. Numeriramo elemente i
čvorove. Čvorove treba pažljivo numerirati, da matrica sustava
koji ćemo konačno dobiti bude što uža, tj. da pojas oko glavne
dijagonale izvan kojeg su same nule bude što uži. Zatim odaberemo
koordinatne funkcije
![]() tako da
tako da ![]() u čvoru
u čvoru ![]() ima vrijednost
ima vrijednost ![]() a u ostalim čvorovima vrijednost
a u ostalim čvorovima vrijednost ![]() Na
elementima, koji nemaju čvor
Na
elementima, koji nemaju čvor ![]() kao vrh,
kao vrh, ![]() ima vrijednost
ima vrijednost ![]() Na elementima, koji imaju čvor
Na elementima, koji imaju čvor ![]() kao svoj vrh, funkciju
kao svoj vrh, funkciju ![]() definiramo kao polinom prvog stupnja ili viših stupnjeva ako to
zahtijeva problem koji rješavamo. Objasnimo sada na jednom
jednostavnom primjeru metodu konačnih elemenata za problem ravnoteže
membrane.
definiramo kao polinom prvog stupnja ili viših stupnjeva ako to
zahtijeva problem koji rješavamo. Objasnimo sada na jednom
jednostavnom primjeru metodu konačnih elemenata za problem ravnoteže
membrane.
![]()
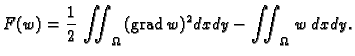
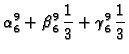
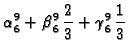
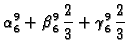
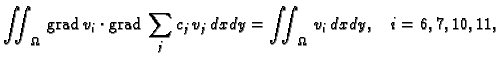
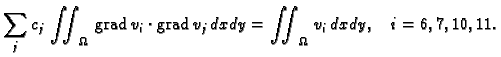
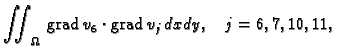 i
i 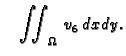
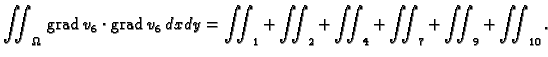
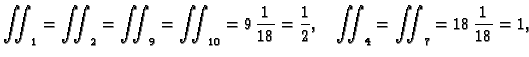

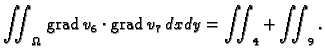
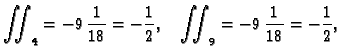

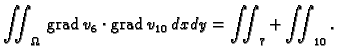
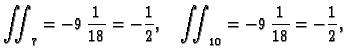
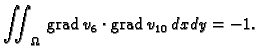
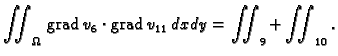
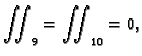
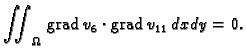
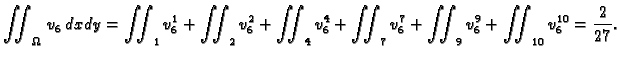
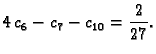
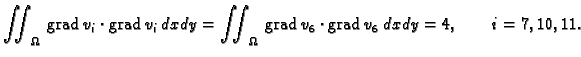
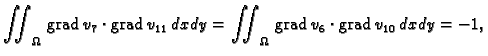
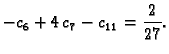
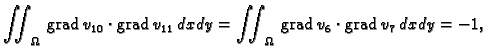
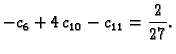
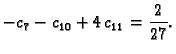
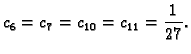
![]() Na pr. u dekadskom sustavu je
Na pr. u dekadskom sustavu je ![]() a u
binarnom
a u
binarnom ![]() Računati ne možemo s beskonačno mnogo
znamenaka. To ne može niti kompjuter. Dapače, on je ograničen
svojim fizičkim mogućnostima, hardwareom. Ograničenje se odnosi na
broj znamenaka
Računati ne možemo s beskonačno mnogo
znamenaka. To ne može niti kompjuter. Dapače, on je ograničen
svojim fizičkim mogućnostima, hardwareom. Ograničenje se odnosi na
broj znamenaka ![]() koje može upotrebiti za zapis jednog broja. Broj
koje može upotrebiti za zapis jednog broja. Broj
![]() se zove preciznost. Uređeni par
se zove preciznost. Uređeni par ![]() zove se
format.
zove se
format.
![]() ili
ili
![]() Dakle radi se o brojevima koji se zapisuju pomoću znamenki
0 i
Dakle radi se o brojevima koji se zapisuju pomoću znamenki
0 i ![]() razmještenih na
razmještenih na ![]() ili
ili ![]() mjesta. Pri tom se prvo
mjesto koristi za predznak. Broj 0 označava pozitivan broj,
mjesta. Pri tom se prvo
mjesto koristi za predznak. Broj 0 označava pozitivan broj, ![]() negativan. Pojedino mjesto na koje možemo upisati jednu znamenku zove
se bit.
negativan. Pojedino mjesto na koje možemo upisati jednu znamenku zove
se bit.
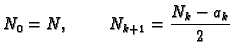 za
za
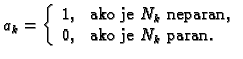
![]() dekadski broj
dekadski broj ![]() zapisuje kao
zapisuje kao
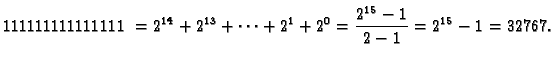
![]() ili
ili
![]() Za prvi format se kaže da se radi o jednostrukoj, a za
drugi o dvostrukoj preciznosti.
Za prvi format se kaže da se radi o jednostrukoj, a za
drugi o dvostrukoj preciznosti.
![]() realni broj se zapisuje u obliku
realni broj se zapisuje u obliku
![]() se ne može točno zapisati u formatu s bazom
se ne može točno zapisati u formatu s bazom ![]() bez obzira kolika
bila preciznost.
bez obzira kolika
bila preciznost.
![]() dan je ovim algoritmom.
dan je ovim algoritmom.
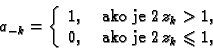
![]() glasi
glasi
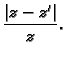
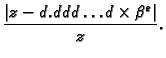
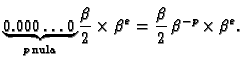
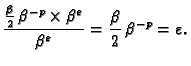
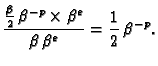
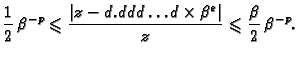
![]() onda se greška u ulpima izražava formulom
onda se greška u ulpima izražava formulom
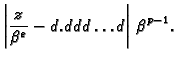
![]() Zatim
Zatim ![]() Odatle
Odatle
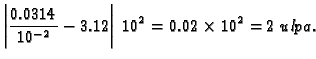
![]() broja
broja ![]() Ako je greška
Ako je greška ![]() ulpa, onada
je broj nepouzdanih znamenki
ulpa, onada
je broj nepouzdanih znamenki
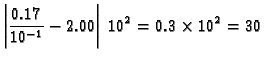 ulpa.
ulpa.
![]() a greška zaokruživanja broja
a greška zaokruživanja broja ![]() je
je
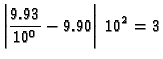 ulpa.
ulpa.
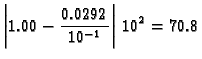 ulpa.
ulpa.
![]() ulpa.
ulpa.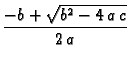
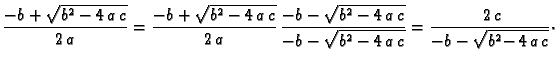
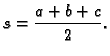
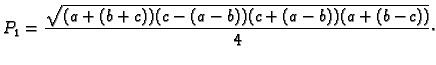
![]() onda imamo
onda imamo
![]() i preciznosti
i preciznosti ![]() Za broj
Za broj ![]() ili
ili ![]() jasno je kako ćemo ga
zaokružiti. Ako je znamenka koja se odbacuje manja od
jasno je kako ćemo ga
zaokružiti. Ako je znamenka koja se odbacuje manja od ![]() onda se
prethodna znamenka ne mijenja. Ako je znamenka koja se odbacuje veća
od
onda se
prethodna znamenka ne mijenja. Ako je znamenka koja se odbacuje veća
od ![]() onda se prethodna znamenka uveća za jedan. Postavlja se
pitanje kako zaokružiti broj
onda se prethodna znamenka uveća za jedan. Postavlja se
pitanje kako zaokružiti broj ![]() ? Jedan način je da se prethodna znamenka uveća za jedan. To može dovesti do velike greške.
? Jedan način je da se prethodna znamenka uveća za jedan. To može dovesti do velike greške.
![]()
![]()
![]() Imamo
Imamo ![]()
![]() prva znamenka
koja se odbacuje, u pola slučajeva zaokružuju odbacivanjem, a u
drugih pola uvećavanjem prethodne znamenke za jedan. Pravilo može
biti na pr. sljedeće.
prva znamenka
koja se odbacuje, u pola slučajeva zaokružuju odbacivanjem, a u
drugih pola uvećavanjem prethodne znamenke za jedan. Pravilo može
biti na pr. sljedeće.