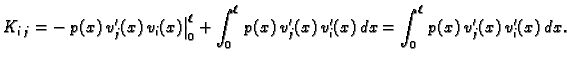



Next: Parcijalne diferencijalne jednadžbe
Up: Numerička matematika
Previous: Aproksimacija funkcije i numerička
Contents
Index
Subsections
Rješavanje
običnih diferencijalnih jednadžbi
Problem početnog uvjeta (Cauchyjev problem)
Želimo riješiti diferencijalnu jednadžbu
na segmentu ![$ [a,b]$](img2505.gif) uz početni uvjet
uz početni uvjet
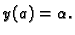
Metode približnog rješavanja koje ćemo sada opisati osnivaju se na
sljedećoj ideji. Podijelimo segment ![$ [a,b]$](img2505.gif) na
na  jednakih dijelova
jednakih dijelova
Duljina svakog podsegmenta je
Brojeve 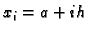 zovemo čvorovima,
a broj
zovemo čvorovima,
a broj 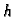 zovemo korakom. Stavimo
Cilj nam je odrediti
zovemo korakom. Stavimo
Cilj nam je odrediti 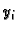 za svaki
za svaki
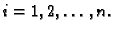 To činimo tako da derivaciju zamijenimo
odgovarajućom algebarskom aproksimacijom, kojom dolazimo do
rekurzivne formule, pomoću koje računamo
To činimo tako da derivaciju zamijenimo
odgovarajućom algebarskom aproksimacijom, kojom dolazimo do
rekurzivne formule, pomoću koje računamo 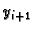 iz poznatog
iz poznatog
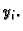 Na taj način, rješenje, koje je neprekidna funkcija,
zamjenjujemo konačnim brojem njezinih vrijednosti. Opisani postupak
se zove diskretizacija. Očekujemo da
će za dovoljno mali
Na taj način, rješenje, koje je neprekidna funkcija,
zamjenjujemo konačnim brojem njezinih vrijednosti. Opisani postupak
se zove diskretizacija. Očekujemo da
će za dovoljno mali 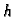 brojevi
brojevi 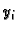 dovoljno dobro aproksimirati
prave vrijednosti funkcije. Važno svojstvo koje diskretizacija treba
imati jeste da s povećanjem
dovoljno dobro aproksimirati
prave vrijednosti funkcije. Važno svojstvo koje diskretizacija treba
imati jeste da s povećanjem  dobivamo sve bolje aproksimacije,
odnosno, preciznije, da brojevi
dobivamo sve bolje aproksimacije,
odnosno, preciznije, da brojevi 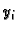 teže prema pravim vrijednostima
funkcije kada
teže prema pravim vrijednostima
funkcije kada
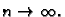
Eulerova metoda
Neka je dana diferencijalna jednadžba
na segmentu ![$ [a,b]$](img2505.gif) uz početni uvjet
uz početni uvjet
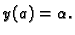
Na temelju Taylorovog teorema
srednje vrijednosti imamo
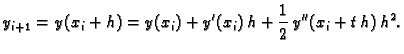 |
(3.23) |
Zanemarimo zadnji član, koji sadrži 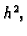 pa dobivamo približnu
vrijednost
Odatle
Tako imamo sljedeći algoritam
pa dobivamo približnu
vrijednost
Odatle
Tako imamo sljedeći algoritam
Algoritam 11
(Eulerova metoda)
Izaberemo dovoljno velik prirodni broj
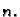
Za zadani korak
računamo niz brojeva
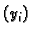
po formuli
s tim da je
a početna vrijednost
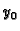
je određena početnim uvjetom.
Mathematica program 6
(Eulerova metoda)
f[x_,y_]=; (* upisuje se f(x,y), ako je jednadzba y'=f(x,y) *)
pocuvj=; (* pocetni uvjet u obliku {x0,y0} *)
kraj=; (* drugi rub segmenta na kojem se trazi rjesenje *)
n=; (* broj podsegmenata podjele *)
h=(kraj-pocuvj[[1]])/n;
x=pocuvj[[1]];
y=pocuvj[[2]];
rj={};
While[x-h<kraj,
rj=Append[rj,{x,y}]//N;
y=y+h f[x,y];
x=x+h];
rj
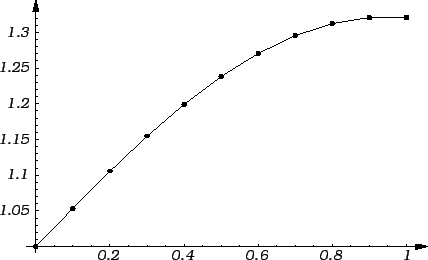
Primjer 3.17
Riješiti Eulerovom metodom Cauchyjev problem
na segmentu
![$ [0,1],$](img3190.gif)
dijeleći ga na deset dijelova.
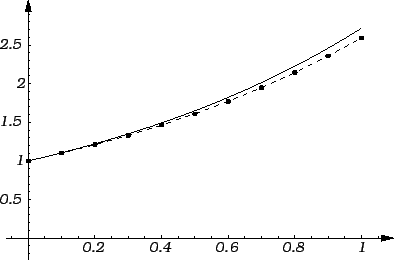
Rješenje. Koristeći se ovim programom, dobivamo sljedeće točke grafa.
Rezultat se vidi na slici. Puna linija predstavlja graf točnog
rješenja
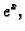
a crtkana linija spaja nađene točke dijelovima
pravaca.
Ova metoda je vrlo jednostavna, ali i vrlo gruba (ocjena pogreške je
vrlo gruba) tako da se rijetko kada upotrebljava.
Metoda Runge-Kutta
U metodi Runge-Kutta se također računa 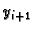 pomoću već
poznate vrijednosti
pomoću već
poznate vrijednosti 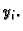 Taj račun je točniji, jer
uzima u obzir i neke međuvrijednosti funkcije
Taj račun je točniji, jer
uzima u obzir i neke međuvrijednosti funkcije 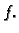 Imamo
sljedeći algoritam
Imamo
sljedeći algoritam
Algoritam 12
(Metoda
Runge-Kutta)
Izaberemo dovoljno velik prirodni broj
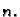
Za zadani korak
računamo niz brojeva
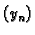
po formuli
Početna vrijednost
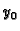
je određena početnim
uvjetom.
Radi bolje preglednosti prilikom računanja se može koristiti
sljedeća tabela.
Mathematica program 7
(Metoda Runge-Kutta)
f[x_,y_]=; (* zadavanje f(x,y), ako je y'=f(x,y) *)
x=;y=; (* po\1etni uvjet *)
h=; (* korak *)
rj={{x,y}};
br=0; (* po\1etna vrijednost broja\1a *)
n=; (* broj koraka *)
While[br<n,
k1=h f[x,y];
k2=h f[x+h/2,y+k1/2];
k3=h f[x+h/2,y+k2/2];
k4=h f[x+h,y+k3];
br=br+1;
x=x+h;
y=y+(k1+2 k2+2 k3+k4)/6;
rj=Append[rj,{x,y}]];
N[rj,10] (* ispis rezultata s deset znamenaka *)
Primjer 3.18
Riješiti isti zadatak kao u primjeru
3.17 metodom
Runge-Kutta.
Rješenje. Primijenimo li gornji program, koji slijedi algoritam metode
Runge-Kutta, dobivamo sljedeće točke grafa rješenja.
Egzaktno rješenje je 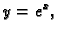 ispisano s deset znamenaka
ispisano s deset znamenaka
Odmah možemo uočiti mnogo bolju točnost nego kod metode Eulera.
Postoji cijela familija metoda zasnovanih na ideji da se podsegment
podijeli na još manje dijelove kako bi se izračunala vrijednost u
sljedećem čvoru. Sve one nose naziv Runge-Kutta metode. Opisani
postupak se najčešće upotrebljava.
Rubni problem
Metoda konačnih diferencija
Neka je dan rubni problem
Podijelimo segment
![$ [0,\ell{}]$](img1456.gif) na
na  jednakih podsegmenata.
Točke
jednakih podsegmenata.
Točke
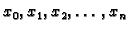 se zovu čvorovi. Točke
se zovu čvorovi. Točke
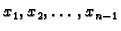 se zovu unutrašnji čvorovi, a
se zovu unutrašnji čvorovi, a
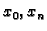 se zovu rubni čvorovi.
Svaki segment ima duljinu
se zovu rubni čvorovi.
Svaki segment ima duljinu
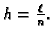 Broj
Broj 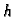 se zove
korak. On se izabire malen, da točnost bude veća, ali sa
smanjivanjem koraka se javljaju drugi nepoželjni efekti, pa u odabiru
koraka treba biti oprezan. Ideja metode se sastoji u tome da se u
svakom čvoru diferencijalna jednadžba zamijeni odgovarajućom
algebarskom jednadžbom i zatim riješi tako dobiveni sustav
algebarskih jednadžbi. U tu svrhu treba derivacije zamijeniti
odgovarajućim algebarskim aproksimacijama. Rješenje koje tako
dobijemo predstavlja približne vrijednosti rješenja u
čvorovima.
se zove
korak. On se izabire malen, da točnost bude veća, ali sa
smanjivanjem koraka se javljaju drugi nepoželjni efekti, pa u odabiru
koraka treba biti oprezan. Ideja metode se sastoji u tome da se u
svakom čvoru diferencijalna jednadžba zamijeni odgovarajućom
algebarskom jednadžbom i zatim riješi tako dobiveni sustav
algebarskih jednadžbi. U tu svrhu treba derivacije zamijeniti
odgovarajućim algebarskim aproksimacijama. Rješenje koje tako
dobijemo predstavlja približne vrijednosti rješenja u
čvorovima.
Uočimo jedan unutrašnji čvor 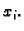 Koristit ćemo sljedeće oznake
Koristit ćemo sljedeće oznake
Na isti način kao u 3.5.1 imamo
Odatle
Ova aproksimacija derivacije se zove aproksimacija s
desna.
Umjesto aproksimacije s desna ponekad se koriste aproksimacija s
lijeva ili centralna aproksimacija. Polazeći od formule
(3.23), u kojoj zamjenimo 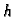 s
s 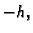
dobivamo, zanemarivanjem člana s 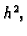 aproksimaciju s lijeva
Centralnu aproksimaciju dobivamo, ako Taylorove formule
za
aproksimaciju s lijeva
Centralnu aproksimaciju dobivamo, ako Taylorove formule
za 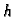 i
i 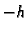 oduzmemo i podijelimo s
oduzmemo i podijelimo s 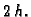 Tada imamo
pa ako zanemarimo član s
Tada imamo
pa ako zanemarimo član s 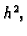 dobivamo
Za aproksimaciju druge derivacije, uzimamo
Zbrojimo ove jednakosti
Podijelimo s
dobivamo
Za aproksimaciju druge derivacije, uzimamo
Zbrojimo ove jednakosti
Podijelimo s 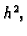 i izračunamo
i izračunamo 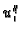 Zanemarimo zadnji član s faktorom
Zanemarimo zadnji član s faktorom 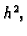 i dobivamo
i dobivamo
U čvoru 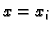 diferencijalna jednadžba iz rubnog problema glasi
diferencijalna jednadžba iz rubnog problema glasi
Zamijenimo li drugu derivaciju s njezinom aproksimacijom, dobijemo
algebarsku jednadžbu za 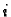 -ti čvor
Pomnožimo jednadžbu s
-ti čvor
Pomnožimo jednadžbu s 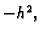 pa imamo
U rubnim čvorovima imamo zadan rubni uvjet. Tako je na lijevom rubu
pa imamo
U rubnim čvorovima imamo zadan rubni uvjet. Tako je na lijevom rubu
Na taj način smo dobili sustav od 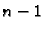 -ne linearne algebarske
jednadžbe. Rubni uvjeti imaju utjecaja samo na prvu jednadžbu
-ne linearne algebarske
jednadžbe. Rubni uvjeti imaju utjecaja samo na prvu jednadžbu
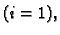 koja postaje, zbog (3.24),
i na zadnju jednadžbu
koja postaje, zbog (3.24),
i na zadnju jednadžbu 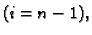 koja, zbog (3.25),
postaje
Sustav možemo zapisati u matričnom obliku. Ako uzmemo
prirodan poredak jednadžbi počevši od čvora
koja, zbog (3.25),
postaje
Sustav možemo zapisati u matričnom obliku. Ako uzmemo
prirodan poredak jednadžbi počevši od čvora 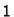 preko
preko 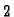 sve do
sve do
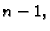 imamo vektor nepoznanica
matricu sustava
i vektor desne strane
Tada sustav možemo zapisati matrično
imamo vektor nepoznanica
matricu sustava
i vektor desne strane
Tada sustav možemo zapisati matrično
Za kvadratnu matricu
![$ A=[a_{ij}]$](img62.gif) kažemo da je
striktno dijagonalno dominantna ako je
kažemo da je
striktno dijagonalno dominantna ako je
Može se pokazati da iz striktne dijagonalne dominantnosti matrice  slijedi njezina regularnost. Ako je
slijedi njezina regularnost. Ako je
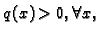 onda je
matrica
onda je
matrica 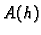 striktno dijagonalno dominantna, pa je regularna. Prema
tome postoji jedinstveno rješenje.
striktno dijagonalno dominantna, pa je regularna. Prema
tome postoji jedinstveno rješenje.
Primjer 3.19
Riješiti metodom konačnih diferencija sljedeći rubni problem
Rješenje. Podijelimo segment
![$ [0,1]$](img3096.gif)
na deset jednakih dijelova, tako da
je korak
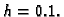
Čvorovi su
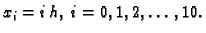
Stavimo
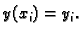
Za prvu derivaciju upotrebimo desnu
aproksimaciju, osim na desnom rubu, gdje uzmemo lijevu. U svakom
unutrašnjem čvoru zamijenimo derivacije odgovarajućim
aproksimacijama. Dobivamo sustav jednadžbi
čije rješenje je
Točke rješenja na sljedećoj slici spojene su ravnim linijama.
Ritzova metoda
Iz varijacijskog principa slijedi da se umjesto rješavanja jednadžbe,
rješenje rubnog problema može dobiti rješavanjem problema
minimizacije odgovarajućeg funkcionala.
Ima raznih metoda koje koriste varijacijsku formulaciju. Jedna od njih
je Ritzova. Pogledajmo kako ona funkcionira kad se radi o rubnom
problemu
gdje je 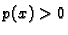 za svaki
za svaki 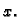
Izaberemo  linearno nezavisnih funkcija
linearno nezavisnih funkcija
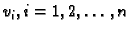 koje
zadovoljavaju Dirichletov homogeni rubni uvjet. Dakle
koje
zadovoljavaju Dirichletov homogeni rubni uvjet. Dakle 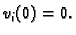 Rješenje se pretpostavi u obliku
Rješenje se pretpostavi u obliku
i neodređeni koeficijenti 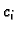 se odrede iz uvjeta da
se odrede iz uvjeta da 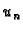 minimizira
pripadni funkcional energije
Tako
dobiveni
minimizira
pripadni funkcional energije
Tako
dobiveni 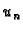 leži u vektorskom prostoru razapetom s funkcijama
leži u vektorskom prostoru razapetom s funkcijama
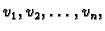 tj. u vektorskom prostoru svih linearnih
kombinacija funkcija
tj. u vektorskom prostoru svih linearnih
kombinacija funkcija
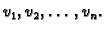 Rješenje ne mora biti
linearna kombinacija tih funkcija, pa u tom slučaju
Rješenje ne mora biti
linearna kombinacija tih funkcija, pa u tom slučaju 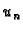 nije točno
već samo približno rješenje. No, grešku koju tom pretpostavkom
činimo, možemo umanjiti uzimanjem većeg
nije točno
već samo približno rješenje. No, grešku koju tom pretpostavkom
činimo, možemo umanjiti uzimanjem većeg 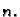
Prvi problem s kojim se susrećemo kod Ritzove metode je određivanje
funkcija 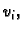 koje se često zovu koordinatne funkcije. One
se obično biraju u skladu s problemom koji se rješava. Na pr. ako
iz fizikalnih razloga očekujemo periodičko rješenje, onda ćemo
takvima pretpostaviti i funkcije
koje se često zovu koordinatne funkcije. One
se obično biraju u skladu s problemom koji se rješava. Na pr. ako
iz fizikalnih razloga očekujemo periodičko rješenje, onda ćemo
takvima pretpostaviti i funkcije 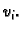 Inače se za koordinatne
funkcije mogu koristiti polinomi.
Inače se za koordinatne
funkcije mogu koristiti polinomi.
Nakon što smo izabrali funkcije
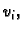 pretpostavljeno rješenje uvrstimo u funkcional
pretpostavljeno rješenje uvrstimo u funkcional
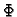 je derivabilna
funkcija od
je derivabilna
funkcija od  varijabli
varijabli
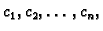 pa jednadžbe
za
pa jednadžbe
za
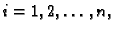 predstavljaju nužan uvjet za ekstrem funkcije
predstavljaju nužan uvjet za ekstrem funkcije 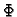 u točki
u točki
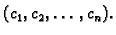 Ovo je sustav od
Ovo je sustav od  linearnih algebarskih
jednadžbi s
linearnih algebarskih
jednadžbi s  nepoznanica. Ako stavimo
dobivamo sustav jednadžbi
On se može matrično zapisati
nepoznanica. Ako stavimo
dobivamo sustav jednadžbi
On se može matrično zapisati
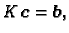 |
(3.26) |
gdje je
![$ K = [K_{ij}],\; \boldsymbol{c}=[c_j],\;
\boldsymbol{b}=[b_i].$](img3337.gif)
Matrica 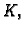 koja se inače zove matrica krutosti, je očito
simetrična, jer je
koja se inače zove matrica krutosti, je očito
simetrična, jer je
Ona je i pozitivno definitna. Doista,
Budući da je 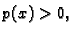 za svaki
za svaki 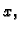 ovaj integral se može poništavati samo tako da bude
odnosno
Odatle
a kako je
ovaj integral se može poništavati samo tako da bude
odnosno
Odatle
a kako je
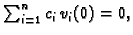 slijedi
slijedi 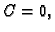 odnosno
Zbog linearne nezavisnosti koordinatnih
funkcija
odnosno
Zbog linearne nezavisnosti koordinatnih
funkcija 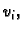 slijedi da je
slijedi da je 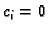 za svaki
za svaki 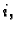 tj.
tj.
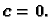 Dakle
Dakle
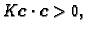 za
za
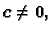 pa je matrica
pa je matrica 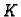 pozitivno definitna.
pozitivno definitna.
Kao što smo vidjeli, takva
matrica se može dijagonalizirati i ima pozitivne vlastite
vrijednosti. To znači da je regularna. Zaista, neka su njezine
vlastite vrijednosti
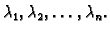 Tada je
Tada je
Odatle slijedi
da jednadžba (3.26) ima jedno i samo jedno rješenje.
Nedostak ove metode je u tome što je matrica 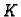 puna matrica, tj.
općenito je svaki njezin element različit od nule.
puna matrica, tj.
općenito je svaki njezin element različit od nule.
Primjer 3.20
Riješimo Ritzovom metodom sljedeći rubni problem
Rješenje. Za koordinatne funkcije uzmimo polinome. Budući da na lijevom
rubu imamo homogen Dirichletov uvjet, polinomi se moraju
poništavati u nuli. Neka su, dakle, koordinatne funkcije
Rješenje pretpostavljamo u obliku
Kad s
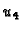
uđemo u funkcional, i njegove derivacije po koeficijentima
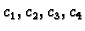
izjednačimo s nulom, dobivamo sustav jednadžbi
Odavde dobijemo za koeficijente
pa je rješenje
Točno rješenje je
Greška računata u točkama
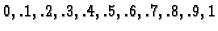
iznosi
Metoda konačnih elemenata
Metoda konačnih elemenata je modifikacija Ritzove metode u tom smislu
da što više elemenata matrice krutosti bude jednako nuli. Budući da
su elementi matrice krutosti
funkcije 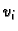 treba birati
tako da međusobni produkti njihovih derivacija budu nulfunkcije u
što više slučajeva.
treba birati
tako da međusobni produkti njihovih derivacija budu nulfunkcije u
što više slučajeva.
Pogledajmo na primjeru kako se to radi. Neka je dan rubni problem
Podijelimo segment ![$ [0,\ell{}]$](img1456.gif) na
na  jednakih dijelova. Time smo dobili
čvorove
gdje je
korak diskretizacije. Rješenje tražimo u obliku
gdje su
jednakih dijelova. Time smo dobili
čvorove
gdje je
korak diskretizacije. Rješenje tražimo u obliku
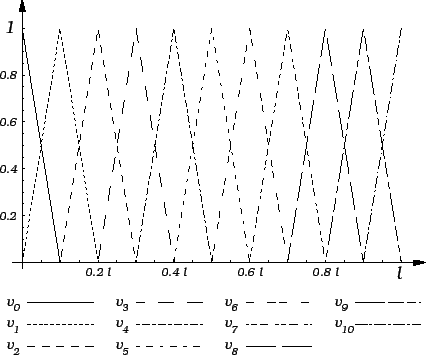
gdje su 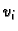 koordinatne funkcije definirane formulom
koordinatne funkcije definirane formulom
![% latex2html id marker 40985
$\displaystyle v_i(x) = \begin{cases}\frac{x}{h} - ...
...o je }x_i\leqslant{}x\leqslant{}x_{i+1} \\ [1mm] 0,& \text{inače}, \end{cases}$](img3381.gif) |
(3.27) |
za
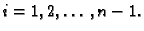 Koordinatne funkcije
Koordinatne funkcije 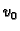 i
i 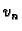 su
definirane ovako
su
definirane ovako
![% latex2html id marker 40993
$\displaystyle v_0(x) = \begin{cases}-\frac{x}{h} +...
...ako je }x_{0}\leqslant{}x\leqslant{}x_1 \\ [1mm] 0,& \text{inače}, \end{cases}$](img3385.gif) |
(3.28) |
![% latex2html id marker 40995
$\displaystyle v_n(x) = \begin{cases}\frac{x}{h} - ...
...o je }x_{n-1}\leqslant{}x\leqslant{}x_n \\ [1mm] 0,& \text{inače}, \end{cases}$](img3386.gif) |
(3.29) |
Rješenje će biti oblika
Imamo
pa je prema tome
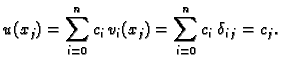 |
(3.30) |
Dakle, neodređeni koeficijenti 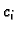 su upravo vrijednosti
približnog rješenja u odgovarajućim čvorovima. Budući da je uvjet
na lijevom rubu homogen, imamo
pa će, prema tome, rješenje biti oblika
Budući da na desnom rubu imamo
prirodni (Neumannov) uvjet, nema nikakvih daljnjih zahtjeva na oblik
rješenja.
su upravo vrijednosti
približnog rješenja u odgovarajućim čvorovima. Budući da je uvjet
na lijevom rubu homogen, imamo
pa će, prema tome, rješenje biti oblika
Budući da na desnom rubu imamo
prirodni (Neumannov) uvjet, nema nikakvih daljnjih zahtjeva na oblik
rješenja.
Iz formule (3.27) slijedi
Odatle dobivamo
![% latex2html id marker 41012
$\displaystyle K_{i\,j} = \int_0^{\ell}\,p\,v'_i\,v...
...x_{i+1}} p(x)\,dx,& \text{ako je }j=i+1 \\ [2mm] 0,& \text{inače}. \end{cases}$](img3394.gif) |
(3.31) |
Dalje radimo isto kao kod Ritzove metode, da bismo na kraju dobili
sustav linearnih algebarskih jednadžbi
Elementi
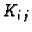 za fiksni
za fiksni 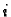 čine
čine 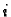 -ti redak matrice krutosti
-ti redak matrice krutosti 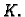 Formula (3.31) nam pokazuje da u jednom retku matrica
Formula (3.31) nam pokazuje da u jednom retku matrica 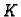 ima
najviše tri elementa različita od nule. To znatno pojednostavnjuje
rješavanje sustava.
ima
najviše tri elementa različita od nule. To znatno pojednostavnjuje
rješavanje sustava.
Primjer 3.21
Riješimo primjer
3.20 metodom konačnih elemenata.
Rješenje. Budući da je uvjet na desnom rubu homogen i prirodan, njega ne
treba uzimati u obzir kod izbora koordinatnih funkcija. Uvjet na
lijevom rubu nam kaže da treba isključiti funkciju 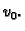 Dakle
rješenje treba tražiti kao
Dakle
rješenje treba tražiti kao
Kad se izračunaju
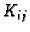
i
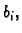
dobije se sljedeći sustav
jednadžbi
Iz ovog sustava se izračunaju koeficijenti
Budući da je rješenje između dva susjedna čvora linearna
kombinacija polinoma prvog stupnja, rezultat će opet biti polinom
prvog stupnja, tj. graf će biti dio pravca. Prema
(
3.30) rješenje je na rubu jednako odgovarajućim
koeficijentima. Tako je za grafički prikaz rješenja dovoljno
nanijeti točke
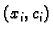
kojima je dodana točka
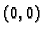
na
lijevom rubu
i zatim te točke spojiti ravnim linijama.
Galerkinova metoda
Galerkinova metoda ili preciznije metoda Bubnova-Galerkina osniva se
na sljedećoj jednostavnoj činjenici. Neka je dan vektorski prostor
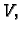 baza
baza
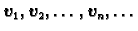 u
u 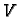 i skalarni produkt u
i skalarni produkt u 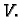 Tada je
Tada je
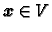 nulvektor, ako i samo ako je
nulvektor, ako i samo ako je
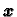 okomit na
okomit na
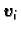 za svaki
za svaki 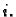 Ta tvrdnja je jasna, ako za
Ta tvrdnja je jasna, ako za 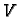 uzmemo vektorski prostor radijvektora u prostoru ili ravnini.
uzmemo vektorski prostor radijvektora u prostoru ili ravnini.
Ono što nas zanima je rubni problem, na pr.
Rješenje tražimo u skupu 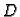 funkcija koje su klase
funkcija koje su klase
![$ C^2([0,\ell]),$](img3427.gif) i koje
zadovoljavaju rubne uvjete. Taj skup nije vektorski prostor, jer
linearne kombinacije takvih funkcija više ne zadovoljavaju ove rubne
uvjete. Međutim, ako su rubni uvjeti homogeni, onda skup
i koje
zadovoljavaju rubne uvjete. Taj skup nije vektorski prostor, jer
linearne kombinacije takvih funkcija više ne zadovoljavaju ove rubne
uvjete. Međutim, ako su rubni uvjeti homogeni, onda skup 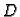 jeste vektorski prostor. Homogenizacijom rubnih uvjeta možemo
svaki rubni problem svesti na problem s homogenim
uvjetima.
jeste vektorski prostor. Homogenizacijom rubnih uvjeta možemo
svaki rubni problem svesti na problem s homogenim
uvjetima.
Promatrajmo dakle rubni problem
U skupu 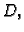 koji je sada vektorski prostor, definirajmo skalarni
produkt
Izaberimo u
koji je sada vektorski prostor, definirajmo skalarni
produkt
Izaberimo u 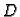 linearno nezavisne funkcije
tako da čine bazu u
linearno nezavisne funkcije
tako da čine bazu u 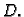 U pravilu funkcija
U pravilu funkcija 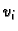 ima beskonačno
mnogo. Neka je
ima beskonačno
mnogo. Neka je  rješenje rubnog problema. Tada je
rješenje rubnog problema. Tada je 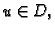 i
prema tome postoje brojevi
i
prema tome postoje brojevi
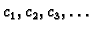 takvi da je
U diferencijalnoj
jednadžbi rubnog problema, funkcija
takvi da je
U diferencijalnoj
jednadžbi rubnog problema, funkcija
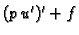 je jednaka
nulfunkciji. To možemo na drugi način iskazati tako da zahtijevamo
da je funkcija
je jednaka
nulfunkciji. To možemo na drugi način iskazati tako da zahtijevamo
da je funkcija
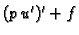 okomita na
okomita na 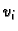 za svaki
za svaki 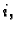 pa
nepoznati koeficijenti
pa
nepoznati koeficijenti 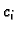 moraju zadovoljavati sljedeće jednadžbe
Problem je u tome što je to beskonačno mnogo
jednadžbi s beskonačno mnogo nepoznanica. Zato uzmemo konačno mnogo
funkcija iz baze
i rješenje pretpostavimo u obliku
Nepoznate koeficijente
moraju zadovoljavati sljedeće jednadžbe
Problem je u tome što je to beskonačno mnogo
jednadžbi s beskonačno mnogo nepoznanica. Zato uzmemo konačno mnogo
funkcija iz baze
i rješenje pretpostavimo u obliku
Nepoznate koeficijente
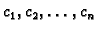 određujemo iz sustava
jednadžbi
Ovaj sustav jednadžbi možemo prepisati u obliku
Stavimo
Tada sustav poprima oblik
odnosno matrično
određujemo iz sustava
jednadžbi
Ovaj sustav jednadžbi možemo prepisati u obliku
Stavimo
Tada sustav poprima oblik
odnosno matrično
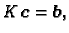 |
(3.32) |
gdje je
![$ K = [K_{ij}],\; \boldsymbol{c}=[c_j],\;
\boldsymbol{b}=[b_i].$](img3337.gif)
U ovom slučaju se u formuli za 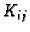 može jednom parcijalno
integrirati pa, uzevši u obzir rubne uvjete, imamo
može jednom parcijalno
integrirati pa, uzevši u obzir rubne uvjete, imamo
Na taj
način sustav jednadžbi (3.32) postaje identičan
onome kod Ritzove metode. To se događa ako rubni problem ispunjava
određene uvjete, o čemu ovdje nećemo detaljnije govoriti.
Istaknimo ovdje bitnu razliku u ideji između Ritzove i Galerkinove
metode. Nužan uvjet za primjenu Ritzove metode je bila egzistencija
varijacijske formulacije rubnog problema u kojoj se pojavljuje
funkcional energije, dok za Galerkinovu metodu to uopće nije važno.
Formalno, Galerkinova metoda se može primijeniti uvijek, pa i u
slučaju nelinearnih rubnih problema. Tada sustav jednadžbi koji
dobijemo nije više linearan.




Next: Parcijalne diferencijalne jednadžbe
Up: Numerička matematika
Previous: Aproksimacija funkcije i numerička
Contents
Index
Salih Suljagic
1999-12-17
![]() na
na ![]() jednakih dijelova
jednakih dijelova
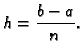
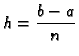
![]() pomoću već
poznate vrijednosti
pomoću već
poznate vrijednosti ![]() Taj račun je točniji, jer
uzima u obzir i neke međuvrijednosti funkcije
Taj račun je točniji, jer
uzima u obzir i neke međuvrijednosti funkcije ![]() Imamo
sljedeći algoritam
Imamo
sljedeći algoritam
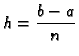
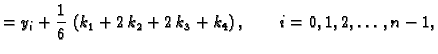
![]() ispisano s deset znamenaka
ispisano s deset znamenaka
![]() Koristit ćemo sljedeće oznake
Koristit ćemo sljedeće oznake
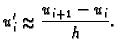
![]() s
s ![]()
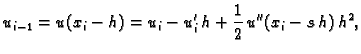
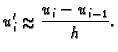
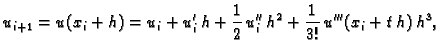
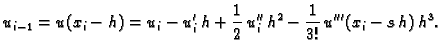
![$\displaystyle u'_i = \frac{u_{i+1}-u_{i-1}}{2\,h} +
\frac{h^2}{3!}\,\left[u'''(x_i+t\,h) + u'''(x_i-s\,h)\right],$](img3272.gif)
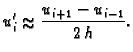
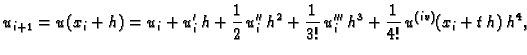
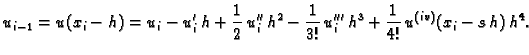
![$\displaystyle u_{i+1} + u_{i-1} = 2\,u_i + u''_i\,h^2 +
\frac{h^4}{4!}\,\left[u^{(iv)}(x_i+t\,h) +
u^{(iv)}(x_i-s\,h)\right].$](img3276.gif)
![$\displaystyle u''_i = \frac{u_{i+1}-2\,u_i+u_{i-1}}{h^2} -
\frac{h^2}{4!}\,\left[u^{(iv)}(x_i+t\,h) +
u^{(iv)}(x_i-s\,h)\right].$](img3278.gif)
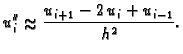
![]() diferencijalna jednadžba iz rubnog problema glasi
diferencijalna jednadžba iz rubnog problema glasi
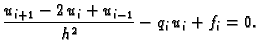
![\begin{displaymath}
% latex2html id marker 40748
A(h) = \left[
\begin{array}{ccc...
...& 0 & 0 & \cdots{} & -1 & (1+h^2\,q_{n-1})
\end{array}\right],\end{displaymath}](img3293.gif)
![]() kažemo da je
striktno dijagonalno dominantna ako je
kažemo da je
striktno dijagonalno dominantna ako je
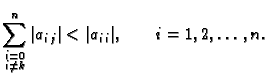
![]() linearno nezavisnih funkcija
linearno nezavisnih funkcija
![]() koje
zadovoljavaju Dirichletov homogeni rubni uvjet. Dakle
koje
zadovoljavaju Dirichletov homogeni rubni uvjet. Dakle ![]() Rješenje se pretpostavi u obliku
Rješenje se pretpostavi u obliku
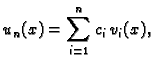
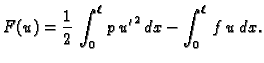
![]() koje se često zovu koordinatne funkcije. One
se obično biraju u skladu s problemom koji se rješava. Na pr. ako
iz fizikalnih razloga očekujemo periodičko rješenje, onda ćemo
takvima pretpostaviti i funkcije
koje se često zovu koordinatne funkcije. One
se obično biraju u skladu s problemom koji se rješava. Na pr. ako
iz fizikalnih razloga očekujemo periodičko rješenje, onda ćemo
takvima pretpostaviti i funkcije ![]() Inače se za koordinatne
funkcije mogu koristiti polinomi.
Inače se za koordinatne
funkcije mogu koristiti polinomi.
![]() pretpostavljeno rješenje uvrstimo u funkcional
pretpostavljeno rješenje uvrstimo u funkcional
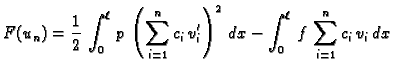
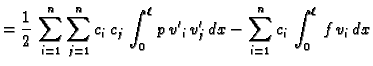
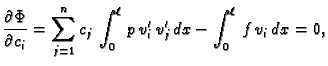
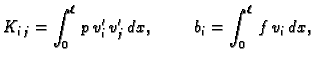
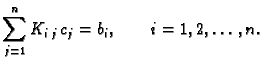
![]() koja se inače zove matrica krutosti, je očito
simetrična, jer je
koja se inače zove matrica krutosti, je očito
simetrična, jer je
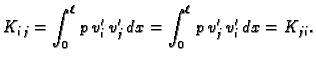
![$\displaystyle K\,\boldsymbol{c}\cdot{}\boldsymbol{c} = \left[\sum_{j=1}^n
K_{ij}\,c_j\right]\cdot{}[c_i] = \sum_{i=1}^n \sum_{j=1}^n
K_{ij}\,c_j\,c_i =$](img3340.gif)
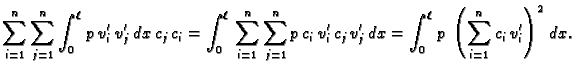
![$\displaystyle \left(\sum_{i=1}^n c_i\,v'_i(x)\right)^2 = 0,\quad \forall x\in [0,\ell],$](img3343.gif)
![$\displaystyle \sum_{i=1}^n c_i\,v'_i(x) = \left(\sum_{i=1}^n c_i\,v_i(x)\right)' = 0,\quad \forall x\in [0,\ell].$](img3344.gif)
![$\displaystyle \sum_{i=1}^n c_i\,v_i(x) = C,\quad \forall x\in [0,\ell],$](img3345.gif)
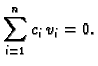
![]() Tada je
Tada je
![]() puna matrica, tj.
općenito je svaki njezin element različit od nule.
puna matrica, tj.
općenito je svaki njezin element različit od nule.
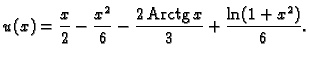
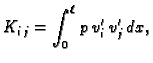
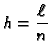
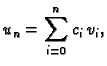
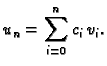
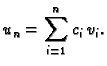
![% latex2html id marker 41010
$\displaystyle v_i'(x) =
\begin{cases}
\frac{1}{h}...
... je }x_i\leqslant{}x\leqslant{}x_{i+1} \\ [1mm]
0,& \text{inače}.
\end{cases}$](img3393.gif)
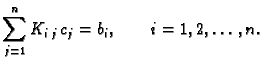
![]() Dakle
rješenje treba tražiti kao
Dakle
rješenje treba tražiti kao
![]() baza
baza
![]() u
u ![]() i skalarni produkt u
i skalarni produkt u ![]() Tada je
Tada je
![]() nulvektor, ako i samo ako je
nulvektor, ako i samo ako je
![]() okomit na
okomit na
![]() za svaki
za svaki ![]() Ta tvrdnja je jasna, ako za
Ta tvrdnja je jasna, ako za ![]() uzmemo vektorski prostor radijvektora u prostoru ili ravnini.
uzmemo vektorski prostor radijvektora u prostoru ili ravnini.
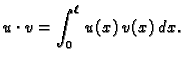
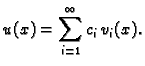
![$\displaystyle \int_0^{\ell}\,\left[\left(p(x)\,\left(\sum_{i=1}^{\infty}
c_i\,v_i(x)\right)'\right)' + f(x)\right]\,v_j(x)\,dx = 0,\qquad
j=1,2,3,\ldots\ .$](img3435.gif)
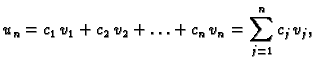
![$\displaystyle \int_0^{\ell}\,\left[\left(p(x)\,\left(\sum_{j=1}^n
c_j\,v_j(x)\right)'\right)' + f(x)\right]\,v_i(x)\,dx = 0,\qquad
i=1,2,3,\ldots,n.$](img3438.gif)
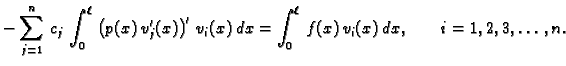
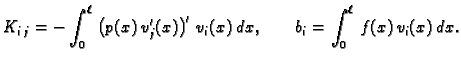
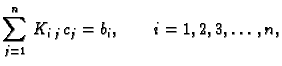
![]() može jednom parcijalno
integrirati pa, uzevši u obzir rubne uvjete, imamo
može jednom parcijalno
integrirati pa, uzevši u obzir rubne uvjete, imamo